九年级数学复习试卷

九年级数学复习试卷

　　　　　　　　　　　　　　 　　　　  姓名　　　　  　 学号　 　

一、选择题（每小题3分，共30分）　　 

1．若分式有意义，则应满足　（　　 ）

A． =0　　B．≠0　　　 C． =1　　　　　 D．≠1

2．方程x(x+1)=3(x+1)的解的情况是　　　　（　　　）

　  A．x=－1　　　B．x=3　　　C． x=－1 、x=3　　　D． 以上答案都不对

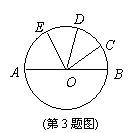3．如图，已知：AB是⊙O的直径，C、D是　 上的三等分点，

∠AOE=，则∠COE是

A. 　　　 B. 　　　 C. 　　　　D.

4．已知实数，，，，,COS,

,0.…(每两个2之间依次多一个0) 中，无理数的个数是（　　 ）

A. 3个　　　　 B.4个　　　　 C. 5个　　　　 D. 6个

5．下列运算正确的是（　 　）

　 　A.  B. C. D.

6.　若抛物线与轴的交点为，则下列说法不正确的是（　　）

A．抛物线开口向上　　　　　　　　　　　　　　 B．抛物线的对称轴是

C．当时，的最大值为　　　　D．抛物线与轴的交点为

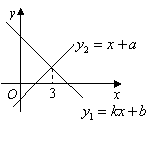7．一次函数与的图象如图，则下列结论 ①；②；③当时，中，正确的个数是（　　）

A．0　　　　　B．1　　　　　　　C．2　　　　　　　D．3

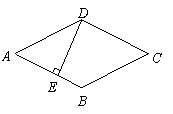
8. 如图，菱形的周长为，，垂足为，，则下列结论正确的有（　　）

①　　　　　　　　 ②

③菱形面积为　　　　　　 ④

Ａ．个　　　 Ｂ．个　　　　　　　Ｃ．个　　　　Ｄ．个

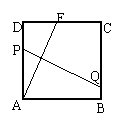9．如下图将边长为12的正方形ABCD的顶点A折叠到DC上

的E点，使DE=5，折痕为PQ，则PQ的长为（　　 ）

　　　 A．12　　　 B． 13　　　C．　14　　　 D． 15

10．已知：二次函数y=x²-4x+a，下列说法错误的是

　　A．当x<1时，y随x的增大而减小

　　B．若图象与x轴有交点，则a≤4

　　C．当a=3时，不等式x²-4x+a>0的解集是1<x<3

　　D．若将图象向上平移1个单位，再向左平移3个单位后过点（1，-2），则a=-3

二、填空题（每小题3分，共24分）

11. 计算：　　　　　 ．

12.不等式组的解集是　　　　　　　  ．

13．如图，P是正三角形 ABC 内的一点，且PA＝6，PB＝8，

PC＝10．若将△PAC绕点A逆时针旋转后，得到△P'AB ，则

点P与点P' 之间的距离为_______，∠APB＝______°．

 

14．用半径为12cm，圆心角为150°的扇形做成一个圆锥模型的侧面，则此圆锥的高为________cm（结果保留根号）．

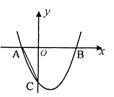15．如图，在平而直角坐标系xOy中，抛物线y=x²+bx+c与x轴交于A、B两点，点A在x轴负半轴，点B在x轴正半轴，与y轴交于点C，且tan∠ACO=，CO=BO，AB=3，则这条抛物线的函数解析式是_________________

16．观察下列等式，……这些等式反映出正整数间的某种规律，用关于n的等式表示出来_______________________.

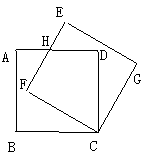
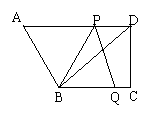
17.如图,边长为3的正方形ABCD绕点C按

顺时针方向旋转30°后得到正方形EFCG，

EF交AD于点H,那么DH的长为　  　.

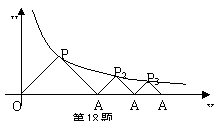
18．如图，△POA₁,△P₂A₁A₂,△P₃A₂A₃,……,△P_nA_n－1A_n都

是等腰直角三角形，点P₁,P₂,P₃,……,P_n在函数(x＞0)的

图象上，斜边OA₁， A₁A₂， A₂A₃,……,A_n－1A_n都在x轴上，则点A₁的坐标是___________，点A₂的坐标是__________，

点A₂₀₀₆的坐标是_______．

三、解答题（共66分）

19．(6分)计算：( )^-1-2sin 45°+ -1

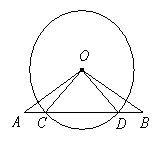
20．（8分）已知：如图，在⊙O中，CD为弦，A、B两点在CD的两端延长线上，且AC=BD。求证：△OAB为等腰三角形

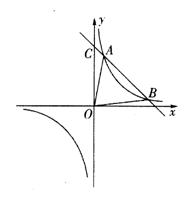
21．（10分）如图已知一次函数和反比例函数

图象在第一象限内有两个不同的公共点A、B．

（1）求实数的取值范围；

（2）若ΔAOB的面积S＝24，求的值．

23. （8分）小刚和小明玩抛掷硬币游戏，其规则是：两人轮流同时抛掷三枚均匀的硬币，如果掷得“两正一反”，那么小刚得6分，否则小明得4分．

　　（1）试用列举法（列表法或画树状图）分析并求出同时抛掷三枚均匀的硬币出现“两正一反”的概率；

　　（2）按照现在的游戏得分规则，你认为该游戏对两人是否公平？请说明理由：如果不公平，请你设计一种得分方式，使这个游戏对两人都公平，并说明理由

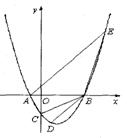24．（10分）设抛物线与x轴交于两个不同的点A(－1，0)、B(m，0)，与y轴交于点C.且∠ACB=90°．

 (1)求m的值和抛物线的解析式；

 (2)已知点D(1，n )在抛物线上，过点A的直线交抛物线于另一点E．若点P在x轴上，以点P、B、D为顶点的三角形与△AEB相似，求点P的坐标．

25．（12分）如图 ，在直角梯形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21。动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动。设运动的时间为t（秒）。

（1）设△BPQ的面积为S，求S与t之间的函数关系式；

（2）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？

（3）当线段PQ与线段AB相交于点O，且2AO＝OB时，求∠BQP的正切值；

（4）是否存在时刻t，使得PQ⊥BD？若存在，求出t的值；若不存在，请说明理由。

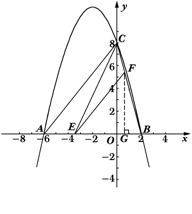
26．（12分）已知抛物线y＝ax²＋bx＋c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB<OC）是方程x²－10x＋16＝0的两个根，且抛物线的对称轴是直线x＝－2．

（1）求A、B、C三点的坐标；

（2）求此抛物线的表达式；

（3）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

（4）在（3）的基础上试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

解：（1）解方程x²－10x＋16＝0得x₁＝2，x₂＝8　

∵点B在x轴的正半轴上，点C在y轴的正半轴上，且OB＜OC

∴点B的坐标为（2，0），点C的坐标为（0，8）

又∵抛物线y＝ax²＋bx＋c的对称轴是直线x＝－2

∴由抛物线的对称性可得点A的坐标为（－6，0）　

（2）∵点C（0，8）在抛物线y＝ax²＋bx＋c的图象上∴c＝8，将A（－6，0）、B（2，0）代入表达式，得

　解得

∴所求抛物线的表达式为y＝－x²－x＋8　　

（3）依题意，AE＝m，则BE＝8－m，

∵OA＝6，OC＝8，∴AC＝10

∵EF∥AC　∴△BEF∽△BAC∴＝　　即＝∴EF＝

过点F作FG⊥AB，垂足为G，则sin∠FEG＝sin∠CAB＝

∴＝　∴FG＝·＝8－m

∴S＝S_△BCE－S_△BFE＝（8－m）×8－（8－m）（8－m）

＝（8－m）（8－8＋m）＝（8－m）m＝－m²＋4m　

自变量m的取值范围是0＜m＜8　　

（4）存在．理由：∵S＝－m²＋4m＝－（m－4）²＋8　　且－＜0，

∴当m＝4时，S有最大值，S_最大值＝8　　

∵m＝4，∴点E的坐标为（－2，0）

∴△BCE为等腰三角形．　　

解：(1)令x=0，得y=－2　 ∴C(0，一2)．∵ACB=90°，CO⊥AB,．

∴ △AOC ∽△COB,．∴OA·OB=OC²；∴

OB=　∴m=4．

解（1）如图3，过点P作PM⊥BC，垂足为M，则四边形PDCM为矩形。∴PM＝DC＝12∵QB＝16－t，∴S＝×12×(16－t)＝96－t

（2）由图可知：CM＝PD＝2t，CQ＝t。热以B、P、Q三点为顶点的三角形是等腰三角形，可以分三种情况：

①若PQ＝BQ。在Rt△PMQ中，，由PQ²＝BQ² 得 ，解得t＝；

A

②若BP＝BQ。在Rt△PMB中，。由BP²＝BQ² 得：

 即。

由于Δ＝－704＜0

∴无解，∴PB≠BQ

③若PB＝PQ。由PB²＝PQ²，得

整理，得。解得（不合题意，舍去）

综合上面的讨论可知：当t＝秒时，以B、P、Q三点为顶点的三角形是等腰三角形。

（3）如图4，由△OAP∽△OBQ，得

∵AP＝2t－21，BQ＝16－t，∴2(2t－21)＝16－t。

∴t＝。

过点Q作QE⊥AD，垂足为E，

∵PD＝2t，ED＝QC＝t，∴PE＝t。

在RT△PEQ中，tan∠QPE＝

（4）设存在时刻t，使得PQ⊥BD。如图5，过点Q作QE⊥ADS，垂足为E。由Rt△BDC∽Rt△QPE，得

，即。解得t＝9

所以，当t＝9秒时，PQ⊥BD。