圆的基本性质（一）
A组
1、
已知：在直角三角ABC中，
,AB=3cm,AC=4cm,AD是CB边上的高，则D在以A为圆心，AC为半径的（ ）
A、圆内 B、圆上 C、圆外 D、无法确定
2、 若AB是⊙O的一条弦，AB=8cm，AB的弦心距为3cm，则⊙O的半径为_____cm。
3、 如图，AB是半径为4cm的⊙O中的弦，且弧AC=弧BC=60°，则AB=_____cm。
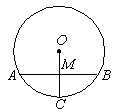
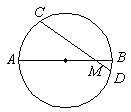
4、 如图，⊙O中的弦CD与直径AB交成30°角，且AM=8cm，BM=2cm，则CD的弦心距=_________cm。
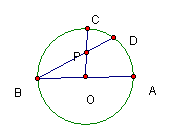
5、 如图所示，⊙O的半径为
，AB是⊙O的直径，半径CO⊥AB,P为CO的中点，则BD=
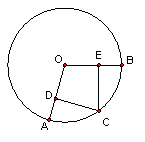
6、如图，四边形ABCD中，∠A=130°，∠B=90°，∠C＝50°，则过四点A、B、C、D能否画一个圆？若能，请画出这个圆，请简单说明理由。（6分）
|
|
8、如图，AB是⊙O的直径，且AD∥OC，若AD的度数为80°。求CD的度数。（6分）
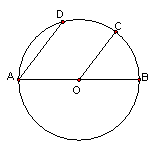
9.如图所示，已知：⊙O的弦AB,E、F是弧AB上两点，弧AE与弧BF相等，OE、OF分别交AB于C、D，求证：AC=BD。
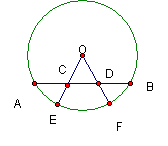
10、如图所示，BC为⊙O的直径，弦AD⊥BC于E，
,求证：
为等边三角形。
B组
11、 如图，弦CD⊥AB于P，AB=8，CD=8，⊙O半径为5，则OP长为________。
12、 在⊙O中，弦CD与直径AB相交于点E，且
，AE=1cm，BE=5cm，那么弦CD的弦心距OF=_________cm，弦CD的长为________cm。
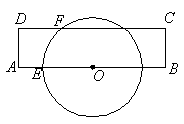
13、 矩形ABCD的边AB过⊙O的圆心，E、F分别为AB、CD与⊙O的交点，若AE=3cm，AD=4cm，DF=5cm，则⊙O的直径等于__________。
14、 ⊙O的半径为10cm，两平行弦AC，BD的长分别为12cm，16cm，则两弦间的距离是（ ）
A. 2cm B. 14cm C. 6cm或8cm D. 2cm或14cm
15、.弓形的半径为10cm，弦长为12cm，则弓高为___________cm.
16、已知扇形面积为12cm2,半径为6cm,则扇形周长为________cm
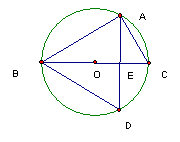
17、 如图，⊙O是
的外接圆，
于F，D为
的中点， E是BA延长线上一点，
，则
等于（ ）
A. 57° B. 38° C. 33° D. 28.5°
18、已知AB、CD是互相垂直的两条弦，OE⊥AD，求证：OE=
BC。
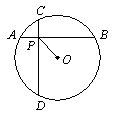
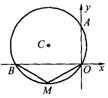
19. 如图，⊙C经过原点且与两坐标轴分别交于点A与点B, 点A的坐标为（0, 4 ) , M是圆上一点，∠BMO=1200．求：⊙C的半径和圆心C的坐标.
。
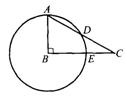
20. 如图，在△ABC中，∠B = Rt∠，∠A
= 600，以点B为圆心，AB为半径画圆，交AC于点D,交BC于点E．求证： (1) AD = 2ED: ( 2 ) D是AC的中点．
C组
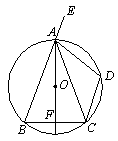
21、如图15，BC是圆O的直径，AD垂直BC于D，弧BA等于弧AF，BF与AD交于E，求证：（1）AE＝BE，（2）若A，F把半圆三等分，BC＝12，求AE的长。
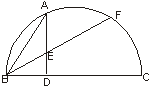图15
22、△ABC内接于⊙O，CE⊥AB于E，交⊙O于F，AD⊥BC，求证：∠FAO=∠BAC。
24、如图，有四个矩形（长，宽均为
），在图（1）中将线段
向右平移1个单位到
，得到封闭图形
，在图（2）中将折线
向右平移1个单位到
，得到封闭图形
。
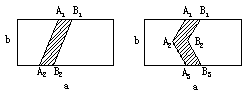
（1） （2） （3） （4）
（1）在图（3）中，请你类似地画一条有两个折点的折线，同样向右平移一个单位，从而得到一个封闭图形，并用斜线画出阴影。
（2）请你分别写出上述三个图形中除去阴影部分后的部分面积：
；
= ；
。
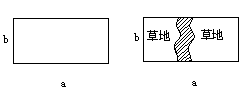
（3）联想与探索
图（4）中，在一块矩形的草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位），请你猜想空白部分表示草地面积是多少？