中考数学摸拟卷2
（赵家初中 毛群芳）
温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！
一、选择题（本题共10小题，每小题4分，共40分.请选出各题中一个符合题意的正确选项，不选、多选、错选均不给分）
1、－2的倒数是（ ）。
A、－2 B、－
C、 D、2
2、要使根式
有意义，则字母x的取值范围是（ ）。
A、x≠5 B、x≤5 C、x＞5 D、x≥5
3、今年6月5日是第33个世界环境日，其主题是“海洋存亡，匹夫有责”．目前全球海洋总面积约为36105.9万平方公里，用科学记数法(保留三个有效数字)表示为
A．3.61×108平方公里 B．3.60×108平方公里
C．361×106平方公里 D．36100万平方公
4、正比例函数y=kx（k≠0）的图象经过点（1,－4），则k的值为（ ）。
A、－4 B、4
C、－
D、
5、如图1中，福娃“迎迎”所骑的自行车的两个车轮（即两个圆）的位置关系是
（A）内含 （B）外离 （C） 相切 （D）相交
6、下列轴对称图形中（如图2），只有两条对称轴的图形是
7、蜗牛前进的速度每秒只有1.5毫米，恰好是某人步行速度的1000分之一，那么此人步行的速度大约是每小时（ ）。
A、9公里 B、5.4公里 C、900米 D、540米
8、中央电视台“非常6 + 1”栏目中有个互动环节，在电视直播现场有三个“金蛋”，三个“银蛋”，其中只有一个“金蛋”内有礼物，银蛋也是如此，有一个打进电话的观众，选择并打开后得到礼物的可能是（ ）。
A、
B、
C、
D、
9、为了美化校园，同学们要在一块正方形空地上种草，他们设计了下图所示的图案，其中阴影部分为绿化面积，哪个图案的绿化面积与其他图案的绿化面积不相等（ ）。
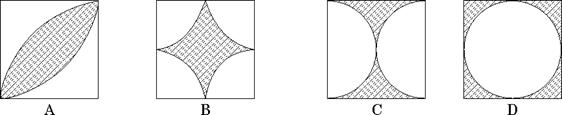
10.若抛物线y＝x2－1998x＋1999与x轴交于点(a,0)、(b,0), 则(a2－1999a＋1999).
(b2－1999b＋1999)的值是( )
A. 1999 B. 1998 C. 3998 D. 3996
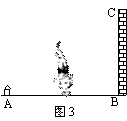二、填空题（共6小题，每小题5分，共30分）
11、不等式3+2x≤－1的解集是 。
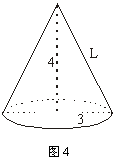
12、如图3，地面A处有一支燃烧的蜡烛(长度不计)，一个
人在A与墙BC之间运动，则他在墙上的投影长度随着
他离墙的距离变小而 (填“变大”、“变小”或“不变”).
 |
13、分解因式：3x2－27= 。
14、如图4，圆锥的底面半径为3cm，高为4cm，那么这个
圆锥的侧面积是 cm2。
| 皮鞋价(元) | 160 | 140 | 120 | 100 |
| 销售百分率 | 60% | 75% | 83% | 95% |
15 某超市购进了一批不同价格的皮鞋，下表是该超市在近几年统计的平均数据. 要
使该超市销售皮鞋收入最大，该超市应多购_____________的皮鞋.
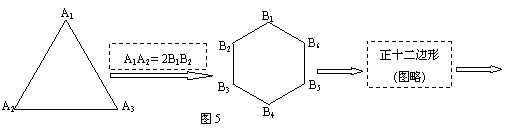
16、如图5，一个正三角形经过变换依次成为正六边形、正十二边形、正二十四边形、….
当这些正多边形的周长都相等时，正六边形的面积 正十二边形的面积(填不等的
符号).
三、解答题（ 本题有8小题，共80 分）
17、（本题满分8分）（1）计算
tan60°+－3 +（6－π）°
（2）解方程：
=
18、（本题满分8分）已知：如图，在平形四边形ABCD中，E、F是对角线AC上的两点，且AE=CF。
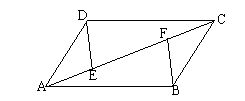求证：DE=BF
证明：
19、
（本题满分8分）大头儿子和小头爸爸用如图所示的两个转盘做游戏，游戏规则如下：
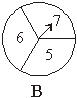分别转两个转盘，当两个转盘所转到的数字之积为偶数时，小头爸爸得1分；
当所转到的数字之积为奇数时，大头儿子得1分。
（1）这个游戏对双方公平吗？通过计算说明理由。
（2）请你只在转盘B上修改其中一个数字，使游戏公平。
20、（本题满分8分）
用四块如图①所示的瓷砖拼成一个正方形的图案，使拼成的图案成一个轴对称图形（如图②），请你分别在图③、图④中各画一种与图②不同的拼法，要求两种拼法各不相同，且其中至少有一个图形既是中心对称图形，又是轴对称图形。
图① 图② 图③ 图④
21、（本题满分10分）为调查我市中学生关于对“感恩”的认识，《衢州日报》某记者抽查了市区几所中学的100名学生，其中一项调查内容是“你如何感激父母的恩情”，调查目的是：“了解学生对父母关爱的回报”，并设置了几个问题，“你记得父母的生日吗？”就是其中的一个问题，在收回的调查问卷后，记者做了数据分析，画出如图所示的统计图，请回答问题：
（1）这次调查中“只记得双亲中一方生日”的学生总共有 人；
（2）在这次调查的所有数据中，“众数”是 ，这个“数”所占的百分数是 ；
（3）就“你如何感激父母的恩情”这个调查内容，你还能为这个记者设置两个问题吗？问题1： ，问题2： .
（4）你想对“父母生日都不记得”的同学说点什么？（不超过15个字）
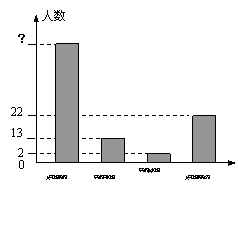
22、（本题满分12分）
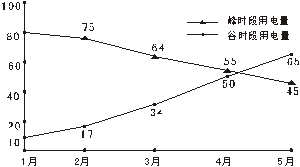小明家使用的是分时电表，按峰时段：（6:00—22:00）和谷时段(22:00—次日6:00)分别计费，峰时段每千瓦时电价为0.61元，谷时段每千瓦时电价为0.30元，小明将家里的2007年1月至5月的峰时段和谷时段的用电量分别折线图表示（如图），同时将前4个月的用电量和相应电费制成表格（如表）：
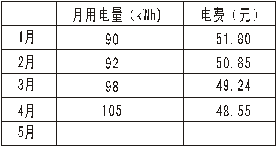
根据上述信息，解答下列问题：
（1）计算5月份的用电量和相应电费，将所得结果填入表中；
（2）小明家这5个月的月平均用电量为 kWh。
（3）小明家这5个月的月平均用电量呈 趋势（选择“上升”或“下降”）；这5个月每月电费呈 趋势（选择“上升”或“下降”）；
（4）小明预计7月份家中用电量很大，估计7月份用电量可达500 kWh，相应电费将达243元，请你根据小时的估计，计算出7月份小明家峰时段用电量和谷时段用电量。
23、（本题满分12分）为了增加农民收入，村委会成立了蘑菇产销联合公司，小明家是公司成员之一，他家五月份收获干蘑菇42．5kg，干香菇35．5kg。按公司收购要求，需将两种蘑菇包装成简装和精装两种型号的盒式装蘑菇共60盒卖给公司。设包装简装型的盒数为x盒，两种型号的盒装蘑菇可获得的总利润为y（元）。包装要求及每盒获得的利润见下表：
| 品种及利润 型号型 | 装入干蘑菇重量（kg） |
装入干香菇重量（kg） |
每盒利润（元） |
| 简装型（每盒） | 0．9 | 0．3 | 14 |
| 精装型（每盒） | 0．4 | 1 | 24 |
(1)写出用含x的代数式表示y的式子。
(2)为满足公司的收购要求，问有哪几种包装方案可供选择？
(3)小明的爸爸想只用这次的收入买一台价值1088元的包装机用于扩大生产，你说能行吗？请证明你的结论．
24、（本题满分14分）已知在平面直角坐标系xoy中，直线y=–3x–3交x轴于点A，交y轴于点C，点B的坐标为（3，0），抛物线y=ax2+bx+c经过A、B、C三点。
（1）求抛物线的解析式。
（2）已知D（4，-1），在抛物线上是否存在点P，使得以线段PD为直径的⊙O‘经过坐标原点O，若点P存在，求出满足条件的点P的坐标；若不存在，说明理由。
（3）已知正方形BEFG的顶点E在x轴上，除B点外，正方形BEFG还有一个顶点在抛物线上，请直接写出E点所有可能的坐标。
祝贺你做完了考题,请再仔细检查一遍,看看有没有错的、漏的,别留下什么遗憾哦!