中考数学摸拟卷

　　　　  淤头初中　 杨爱园

试卷I

一、选择题（本题有10小题，每小题4分，共40分，请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）

1、计算2－7的结果是（　 ）

A、－5　　　B、5　　C、－9　　D、9

2、据统计，2005“超级女声”短信投票的总票数约张，将这个数用科学计数法表示为（　　）

A、3.2682×10⁶　B、3.268×10⁷ C、3.268×10⁸ D、3.268×10⁹

3、已知分式的值是零，那么x的值是（　  ）

A、-1　　　 B、0　　　 C、1　　　 D±1

4、抛物线y=2(x-1)²-2的顶点坐标是（　　）

A（-1，2）　 B、（1，-2）　 C、（-1，2）　 D、（1，2）

B　　  C

5、如图，小正方形的边长均为1，则下列图中的　　　　　 A
三角形（阴影部分）与△ABC相似的是（　　）　

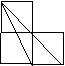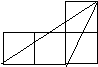A　　　　　  B　　　　  　C　　　　　　 D

6、点A（-5，y）和B（-3，y₂）都在直线y=-2x=1上，则y₁与y₂的大小关系是（　　）

A、y1≤y2　　B、y1=y2　　 C、y1＜y2　　D、y1＞y2

7、如图，一条公路修到湖边时，须拐弯绕湖而行，如果第一次拐的角∠A=120°，第二次拐的角∠B=150°，第三次拐的角是∠C，这时道路恰好和第一次拐弯之前的道路平行，则∠C是（　　）

A、120°　B、150°　C、130°　D、140°　　　　　　　　　

B　　C

E

　　　　　　　　　　　　　　　　　　　　  A

　　　　　　　　　　　　　　　　　　　　　　　　　

8、如图是由几个小立方体所搭几何体的俯视图，小正方形数字表示在该位置的小立方体的个数，这个几何体的主视图是（　　）

2 1　 1　 1

 

A　　　　 B　　　　　  C　　　　　  D　　　　  如图

9、若一个多边形的内角和为外角和的3倍，则这个多边形为（　　）

A、八边形　　 B、九边形　　 C、十边形　　 D、十二边形

10、如图，∠ABC=90°O为射线BC上一点，以点O为圆心，BO长的一半为半径作⊙O，当射线BA绕点B按顺时针方向旋转一定的角度后与⊙O相切，则旋转的度数为（小于180°）（　　）

A、30° B、60° C、30或120° D、60°或120° A

B　　 O　　 C

　　　　　　　　　　　　　　　　　

二、填空题（本题有6小题，每小题5分，共30分）

11、因式分解a²+3a=_________

12、计算sina30°+ tan60°=___________

A

13、如图，PA是⊙O的切线A为切点，PBC是过点O的割线，若PA=8cm，PB=4cm, ⊙O直径为_________

　　　　　　　　　　　　　　　 C　　O　　B　　　　P

14、某校九年级（1）班想举办班徽设计比赛，全班50名同学，计划每位同学交设计方案一份，拟评选出10份为一等奖，那么该班某位同学获一等奖的概率为__________

15、在Rt_△ABC中，∠C=90°，BC=6cm，AC=8cm，动点P从点C出发，以2cm/s的速度沿CA，AB移动到点B，点P点出

发______秒时，可使得S△BCP=S_△ABC。

16、如图,若将宽为3cm的矩形纸片沿AB折叠成∠ACB=45°，那么△ABC的面积为______________。

C

　　 A

　　　　　　　　　　　　　　　　　　　　　　  B

三、解答题（本小题8小题，共80分，第17-20题每题8分，第22-23题每题12分，第24题14分）。

17、（1）（π-1）°+2cos60°+（）²

（2）计算：+

18、先化简代数式（+）÷ ，然后选取一个使原式有意义的a的值代入求值。

16m　　　　　　　　　　　　 16m

19、在一块长16m，宽12m的矩形荒地上，要建造一个花园，要求花园所占面积为荒地面积的一半，图①②分别是小明和小颖的设计方案。

xm　　　　　　　　　　　　 16m

　　　　　　　　　　　 

※ ※ ※ ※ ※ ※ ※ ※ ※

※ ※ ※ ※ ※ ※ ※　※　※

　　 12m　　　　　　　　　　　　 12m

小明　　　　　　　　　　　　　　　　　　　　　　　 小颖

（1）你认为小明的结果对吗？请说明理由。

（2）请你帮助小颖求出图中的力（精确到0.1m）

（3）你还有其他的设计方案吗？请画出你的设计草图。

20、如图，在□ABCD中，BE平分∠ABC，EC⊥BC，BE=2EC

（1）求∠A的度数　　　　　　　　　 A　　　　  E　　D

　　（2）求的值

　　　　　　　　　　　　　　　　　 B　　　　　　　 C

21、某商场门前的台阶截面积如图所示，已知每级台阶的宽度（如CD）均为0.3m，高度（如BE）均为0.2m，现将此台阶改造成供轮椅行走的斜坡，并且设计斜坡的倾斜角∠A为9°，计算从斜坡的起点A到台阶前点B的距离（精确到0.1m）。

　　　　　　　　　　　　　　　　　　　　　　 C　D

　　　　　　　　　　　　　　　　　　　　

　　　　　　　 A　　　　　　　　　　　　 B　　　　 F

22、市教育局为了解我市2007年初中毕业生的体育测试情况，从中抽取了600名毕业生的三项测试的综合成绩（得分取正整数，满分为30分）进行统计，列出频数分布表，绘出频数分布直方图：

等级（分数x/分）	频数	频率
A（x≥27）	180	0.3
B(24≤x≤26)	270	①
C(18≤x≤23)	②	0.25
D(x≤17)	0	0
合　计	③	300 250 200 150 100 50   1.00

　　　　　　　　　　　　　　　　　　　　　　　　　　 A　 B  C　D

请解答下列问题：

（1）完成频数分布表并补全频数分布直方图；

（2）样本的中位数落在______等级；

（3）如果三项测试的成绩A等为优秀，试估计我市71600名毕业生体育成绩优秀的人数约是多少？

23、夏天容易发生腹泻等肠道疾病，益阳市医药公司的甲、乙两仓库内分别存在医治腹泻的药品80箱和70箱，现需要将库存的药品调往南县100箱和沅江50箱，已知从甲、乙两仓库运送药品到两地的药费（元/箱）如下表所示：

县  名	费用（元/箱）
	甲仓库	乙仓库
南  县	14	20
沅  江	10	8

（1）设从甲仓库运送到南县的药品为x箱，求总费用y（元）与x（箱）之间的函数关系式，并写出x的取值范围；

（2）求出最低费用，并说明总费用最低式的调配方案；

24、抛物线y=ax²+2x+3(a<0)交x轴于A、B两点（B在A的右边），交y轴于点C，顶点为D，而且经过点（2，3）

（1）写出抛物线的解析式及C、D两点的坐标

（2）连结BC，以BC为边向右作正方形BCEF，求E、F的坐标，将此抛物线向上平移，试判断平移后的抛物线是否会同时经过正方形BCEF的另两个顶点E、F？若能，写出平移后抛物线的解析式；若不能，请说明理由。

（3）若P是抛物线y=ax²+2x+3上任意一点，过点P作直线垂直于抛物线y=ax²+2x+3的对称轴，垂足为Q，那么是否存在这样的点P，使以P、Q、D为顶点的三角形与△BOE相似？若存在，请求出P点的坐标，若不存在，请说明理由。