九年级下数学月考试卷
一、 精心选一选（共40分）
1、已知二次函数
、 
、 
， 它们的图象开口由小到大的顺序是（ ）
A、
B、
C、
D、
2、已知二次函数y=-x2+bx+c的图象的最高点（-1，-3)，则b与c的值是（ ）
A. b=2, c=4 B. b=2, c＝-4 C. b=-2, c=4 D. b=-2, c＝-4
3、 二次方程ax2+bx +c=0的两根为5和-1 ，则对应的二次函数y=ax2＋bx+c的对称轴是直线（ )
A.x=-2 B. x=2 C. x= 3 D.x=-3
4、直角坐标平面上将二次函数y＝-2(x－1)2－2的图象向左平移１个单位，再向上平移１个单位，则其顶点为（ ）
A.(0，0) B.(1，－2) C.(0，－1) D.(－2，1)
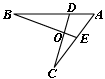
5、如图1，AB∥CD∥EF，则图中相似三角形的对数为（ ）
A、 1对 B、 2对 C、 3对 D、 4对
6、抛物线
与x轴无交点，则ｍ的取值范围是（）
A、ｍ＞
B、ｍ＞
C、ｍ＜ D、ｍ＜
7、如图2，D、E分别是AB、AC上两点，CD与BE相交于点O，
下列条件中不能使ΔABE和ΔACD相似的是 （ ）
A. ∠B=∠C B. ∠ADC=∠AEB
C. BE=CD，AB=AC D. AD∶AC=AE∶AB
8、小颖在二次函数y=2x2+4x+5的图象上，依横坐标找到三点(－1，y1)，
(
，y2)， (－，y3)，则你认为y1，y2，y3的大小关系应为( )
A.y1>y2>y3 B.y2>y3>y1 C.y3>y1>y2 D.y3>y2>y1
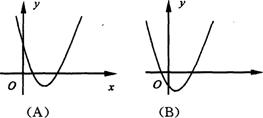9、当a>0, b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是（ ）
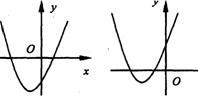
10、已知二次函数
的图象如图3，下列结论（1）2a+b＞0；
（2）a-b+c＞0；（3）4a+2b+c＜0；（4）（a+c）2＜b2，其中正确的是：（ ）
A．1个 B．2个 C．3个 D．4个
 |
 |
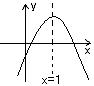
二、 细心填一填（共25）
11、若二次函数y=(m+1)x2+m2-9有最大值,且图象经过原点，则m= 。
12、已知抛物线
与x轴交点的横坐标为 –1，则
= 。
13、请写一个开口向上，对称轴为直线x=2，且与y轴的交点坐标为（0，3）的抛物线的解析式： 。
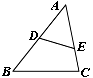
14、如图4，DE与BC不平行，当
= 时，ΔABC与ΔADE相似。
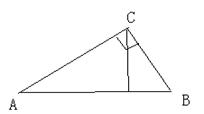
15、如图5，RtDABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，则AD=_________。
 |
三、 认真答一答（共85分）
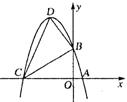
16、（12分）如图，二次函数y=ax2+bx+c的图象经过A 、B、C三点，
（1）观察图象，写出A 、B、C三点的坐标，并求出抛物线解析式，
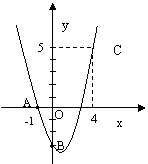（2）求此抛物线的顶点坐标和对称轴。
17、（12分）已知二次函数图象顶点坐标A（2，-1）且图象过点M（5，8），
(1)求二次函数解析式.
(2)设该函数与x轴交与B,C两点，与y轴交于D,求△BCD的面积。
18、（12分）如图，在△ABC中，∠C＝900，CD⊥AB于D。
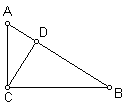（1）、写出图中所有与△ABC相似的三角形。
（2）、试证明：
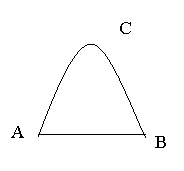19、（10分）某工厂大门是一抛物线水泥建筑物（如图），大门地面宽AB= 4米，顶部C离地面高为
米，现有一辆载满货物的汽车欲通过大门，货物顶点距地面
米，装货宽度为
米，请通过计算，判断这辆汽车能否顺利通过大门？
20、（12分）如图，矩形ABCD中，E为BC上一点，DF⊥AE于F.
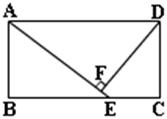(1)ΔABE与ΔADF相似吗？请说明理由.
(2)若AB=6，AD=12，BE=8，求DF的长.
21、（13分）某商店经营一批进价每件为2元的小商品，在市场营销的过程中发现：如果该商品按每件最低价3元销售，日销售量为18件，如果单价每提高1元，日销售量就减少2件．设销售单价为x（元），日销售量为y（件）．
（1）写出日销售量y（件）与销售单价x（元）之间的函数关系式；
（2）设日销售的毛利润（毛利润=销售总额-总进价）为P（元），求出毛利润P（元）与销售单价x（元）之间的函数关系式；
（3）在下图所示的坐标系中画出Ｐ关于x的函数图象的草图，并标出顶点的坐标；
（4）观察图象，说出当销售单价为多少元时，日销售的毛利润最高？是多少？
| |
22、（14分）已知：m、n是方程x2-6x+5=0的两个实数根，且m< n，抛物线y=-x2＋bx+c的图象经过点A(m, O), B(0,n).
(1）求这个抛物线的解析式；
(2）设（1）中的抛物线与x轴的另一个交点为 C，抛物线的顶点为D，试求出点C、 D的坐标和△BCD的面积
（注：抛物线y=ax2+bx+c2（a≠0）的顶点坐标（
）
(3）P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2:3的两部分，请求出P的坐标．
