初三数学自测考试试卷（PE.6）
(考试时间:120分钟 试卷总分:150分 考试形式:闭卷 )
第一部分（共30分）
注意事项:1.答题前务必将姓名、准考证号、科目用铅笔涂写在答题卡上。
2．选出答案后，用铅笔将对应题目的答案标号涂黑，答在试卷上无效。
3．考试结束，将答题卡和试卷一并交回。
一、选择题（每小题3分，共30分）
1.－2的倒数是 （ ）
A.－2 B.
C.
D.2
2.下列计算正确的是 （ ）
A.a3-a2=a B.(a2)3=a5 C.a6÷a2=a3 D.a2·a3=a5
3.函数
中自变量x的取值范围是 （ ）
A.x≥ B.x≠1
C.x≥且x≠-1 D.x≥且x≠1
4.已知关于x的不等式x+m>5的解集如图如示，则m的值为 （ ）
A.2 B.-2
C.8 D、-8
5.解方程
时，如果设
，那么原方程可化为
（ ）
A.y2+3y+2=0 B.y2-3y+2=0
C.y2+3y-2=0 D.y2-3y-2=0
6.下列命题中错误的是 （ ）
A.到线段两端距离相等的点的轨迹是这条线段的垂直平分线.
B.过弦的中点的直径必垂直于弦.
C.过圆心且过切点的直线必垂直于这条切线.
D.正六边形既是轴对称图形又是中心对称图形.
7.已知：两圆的半径分别为7和3，圆心距为10，那么这两个圆的位置关系是 （ ）
A.外切 B.内切 C.相交 D.内含
8.反比例函数
的图象位于（ ）
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
9.若抛物线过点（1，0），且其解析式中二次项系数为1，则它的解析式可以是 （ ）
A.y=2x2-x-1 B.y=x2+3x+4
C.y=-x2-3x+4 D.y=x2-x
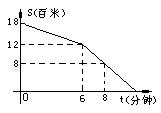10.“高高兴兴上学来，开开心心回家去”，小明某天放学后，17时从学校出发，回家途中离家的路程S（百米）与所走的时间t（分钟）之间的函数关系如图所示，那么这天小明到家的时间为 （ ）
A.17时15分 B.17时14分
C.17时12分 D.17时11分
第二部分（共120分）
二、填空题（每小题3分，共24分）
11.分解因式：a2-4b2=__________________. 第10题
12.若最简根式
与
是同类二次根式，则a=____________.
13.某商厦将标价为100元的商品打8折销售后仍获利10%，则该商品的进价为____________元.
14.温家宝总理在十届全国人大四次会议《政府工作报告》中指出在“十一五”期间公路总里程规划达230万km，请用科学记数法表示总里程为_________km.
15.已知：如图，∠AOB=100°，则∠ACB等于_______________.
 |
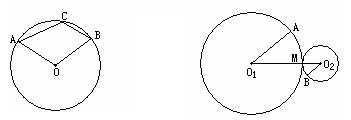第15题 第17题
16.底面半径为2且母线长为4的圆锥的侧面展开图的面积为____________（结果保留π）.
17.如图，⊙O1与⊙O2外切于M，⊙O1的半径为6，⊙O2的半径为2，∠AO1M=40°, O1A∥O2B，则曲线AMB的长等于____________.
18.已知：2+
=22×，3+
，4+
=42×
如果10+
=102×（且a、b为正整数），则ab=____________.
三、解答题（19－24题每小题6分，25题8分，26－29题每小题10分，30题12分）
19.计算
20.先化简再求值：
， 其中
.
21.细心的小丽发现电线杆AB的影子在土坡的坡面CD和地面BC上，量得
CD=8m，BC=20m，CD与地面成30°角，且此时测得1m杆的影长为2m，求
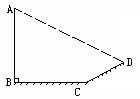电线杆的高度是多少米？
 |
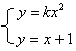22.已知方程组 有两个不相等的实数解.
（1）求k的取值范围；
（2）若方程组有两个实数解为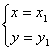
和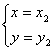
，问是否存在实数k，使
？若存在，求出k的值；若不存在，请说明理由.
23.某市沿河路边有一桥欲维修，拟由甲、乙两个工程队共同完成此工程，
若两个工程队合做24天恰好完成.若两个工程队合作18天后，甲工
程队再单独做10天，也恰好完成.
请问： 甲、乙两个工程队单独完成此工程各需多少天？
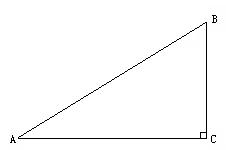
24.如图，△ABC是直角三角形，∠C=90°.
（1）作∠A的平分线，交BC于点M；作线段AM的垂直平分线，交AC于点N；（尺规作图，不写作法，保留作图痕迹）
（2）根据作出的图形填空：当∠BAC=30°时，
的值为___________.
 |
25.某校为了了解初一学生一分钟跳绳次数的情况，抽取了一部分初一学生进行一分钟跳绳次数的测试，将所得数据进行整理，可得如下频率分布表：
| 组别 | 分组 | 频数 | 频率 |
| 1 | 89.5~99.5 | 4 | 0.04 |
| 2 | 99.5~109.5 | 3 | 0.03 |
| 3 | 109.5~119.5 | 46 | 0.46 |
| 4 | 119.5~129.5 | b | c |
| 5 | 129.5~139.5 | 6 | 0.06 |
| 6 | 139.5~149.5 | 2 | 0.02 |
| 合计 | a | 1.00 | |
（1）这个问题中，总体是____________________________________，
样本容量a=________；
（2）第四小组的频数b=_________，频率c=______________；
（3）若次数在110次（含110次）以上为达标，试估计该校初一学生
一分钟跳绳次数的达标率是多少;
（4）在这次测试中，学生跳绳次数的中位数会落在哪个小组内？
26.已知抛物线y=ax2+bx+c经过点（2，1），（-1，-8）,（0，-3）.
（1） 求这个抛物线的解析式；
（2） 画出该抛物线的草图，并标出图象与x轴交点的横坐标；
（3） 
观察所画出的图象，写出x在什么范围内取值时，函数值y<0.
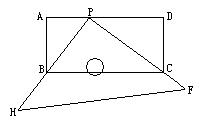
27.如图，有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够
大的直角三角板PHF的直角顶点P落在AD边上（不与点A、D重合），在
AD上适当移动三角板顶点P.
（1）若三角板两直角边分别通过点B与点C时，请你求出这时AP
的长；
（2）再次移动三角板的位置，使三角板顶点P在AD上移动，直角边PH
始终通过点B，另一直角边PF与DC的延长线交于点Q，与BC交于
点E，当CE=2cm时，设AP＝x，CQ＝y，①写出y与x之间的函数
关系式；②求出这时AP的长.（不要求写出自变量的取值范围）
 |
28.房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金
不少于2090万元，但不超过2096万元，且所筹资金全部用于建房，两
种户型的建房成本和售价如下表：
| A | B | |
| 成本（万元/套） | 25 | 28 |
| 售价（万元/套） | 30 | 34 |
（1）该公司对这两种户型住房有哪几种建房方案？
（2）该公司如何建房获得利润最大？
（3）根据市场调查，每套B型住房的售价不会改变，每套A型住房的售
价将会提高a万元（a>0），且所建的两种住房可全部售出，该公司又
将如何建房获得利润最大？（注：利润=售价－成本）
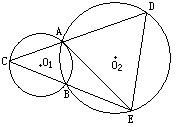
29.已知⊙01和⊙02相交于A、B两点，过A点作⊙01的切线交⊙02于点E，连接EB并延长交⊙01于点C，直线CA交⊙02于点D.
（1）如图，当点D与点A不重合时，试猜想线段EA与ED是否相等？
并证明你的结论；
（2）当点D与点A重合时，直线AC与⊙02有怎样的位置关系？
此时若BC=2，CE=8，求⊙01的直径.
 |
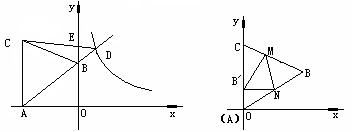
30.如图（1）已知：一次函数y=
x+2的图象与x轴、y轴分别交于A、B，以AB为边在第二象限内作等边△ABC.
（1）直线y= x+2与双曲线y=
在第一象限内交于D点，求点D的坐标；
（2）求△BCD的面积；
（3）如图2，若将△ABC向右平移，使得A点与原点O重合，并将△ABC
折叠，使点B落在边OC上的B′点，折痕为MN.
①求当B′N∥x轴时，点B′和N点的坐标；
②当点B′在OC上运动，但不与点O、C重合时，△B′MN能否为直角
三角形，若能，请求出此时点B′坐标，若不能，请说明理由.
 |
（1） （2）