二次函数实践与探索（四）

二次函数实践与探索（四）

一、填空题　

1.二次函数y= a (x+m)²-m (a≠0) 无论m为什么实数，图象的顶点必在 (　　)

　A.直线y=-x上　　 B. 直线y=x上　　　C.y轴上　　　 D.x轴上

2.如图，在直角三角形AOB中，AB＝OB，且OB=AB=3，设直线，

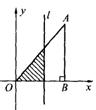截此三角形所得阴影部分的面积为S，则S与t之间的函数关系的图象为 （　　）

　　

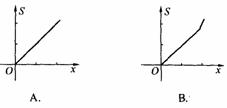
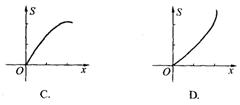
3. 关于二次函数y=ax²+bx+c的图象有下列命题：

① 当c=0时，函数的图象经过原点；

② 当c＞0且函数的图象开口向下时，方程ax²+bx+c=0必有两个不等实根；

③ 函数图象最高点的纵坐标是;

④ 当b=0时，函数的图象关于y轴对称．其中正确的命题的个数有 (　　)

　 A. 1个　　B. 2个　　 C. 3个　　　D. 4个

4. 若一抛物线y=ax²与四条直线x=1，x=2, y =1, y =2 围成的正方形有公共点，则a的取值范围是 (　 )

5、  关于x的方程没有实数根，则的图象的顶点在

A． 第一象限B。第二象限C第三象限D第四象限

6．二次函数的图象上有两点(3，－8)和(－5，－8)，则此拋物线的对称轴是（　　）

A．直线x＝4　　　B. 直线x＝3　　 C. 直线x＝－5　　D. 直线x＝－1。

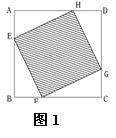7、如图1，已知：正方形ABCD边长为1，E、F、G、H分别为各边上的点， 且AE=BF=CG=DH, 设小正方形EFGH的面积为，AE为，则关于的函数图象大致是

（　　 ）

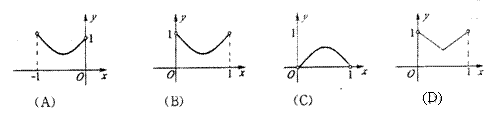8、在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax²+c的图象大致为 （　）

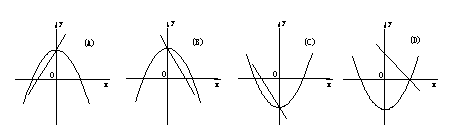
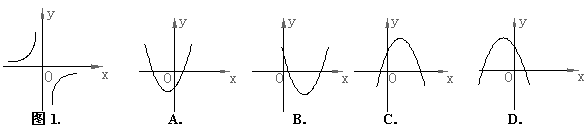9．已知反比例函数　　的图象如图1，则二次函数的图象大致为（　　）

	A．		B．

二、计算题

10. 利用函数的图象求下列方程的解，

(1)x²＋x－6＝0；　　(2)2x²－3x－5＝0

11．利用函数的图象求下列方程的解。

(1)、，　  (2)、

12、已知抛物线y₁＝2x²－8x＋k＋8和直线y₂＝mx＋1相交于点P(3，4m)。

　　(1)求这两个函数的关系式；

　　(3)当x取何值时，抛物线与直线相交，并求交点坐标。

13、今有网球从斜坡O点处抛出，网球的抛物线是的图象的一段，斜坡的截

线OA在一次函数的图象的一段，建立如图所示的直角坐标系。

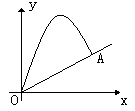求：（1）网球抛出的最高点的坐标。

（2）网球在斜坡的落点A的垂直高度。