九年级（上）数学期末试卷
一选择题：（每道小题3分，共30分）
1.下列等式一定成立的是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
2.时钟上的分针匀速旋转一周需要60min则经过10min，分针旋转了 （ ）
A、100 B、200 C、300 D、600
3.平面直角坐标系内一点P（－2,3）关于原点对称点的坐标是 （ ）
A、（3，－2） B、（2,3） C、（－2，－3） D、（2，－3）
4.若式子
有意义，则x的取值范围为（ ）
（A）x≥2 （B）x≠3 （C）x≥2或x≠3 （D）x≥2且x≠3
5.关于x的一元二次方程kx2-6x+1=0有两个不相等的实数根,则k 的取值范围是( )
A. k≥9
B. k<9;
C. k≤9且k≠0 D.
k<9且k≠0
6.下列图形中，既是轴对称图形又是中心对称图形的是（ ）
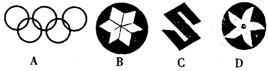图1
图2
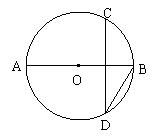
7.如图2所示,EF为⊙O的直径,OE=5cm,弦MN=8cm,那么E、F两点到直线MN的距离之和等于 ( )
A. 12cm B. 8cm C. 6cm D. 3cm
8.下面是李刚同学在一次测验中解答的填空题，其中答对的是（ ）．
A、若x2=4，则x＝2 B、方程x(2x－1)＝2x－1的解为x＝1
C、若x2+2x+k=0的一个根为1，则
D、若分式
的值为零，则x＝1，2
9..关于
的一元二次方程
的一个根是0，则
的值为（ ）
A、1 B 、-1 C、1或-1 D、0.5
10.已知在⊙O中，弦AB的长为8厘米,圆心O到AB的距离为3厘米, 则⊙O的半径是（ ）
A.3厘米 B. 4厘米 C. 5厘米 D. 8厘米
11．下列关于x的方程中，是一元二次方程的有（ ）
A． 
B．
C． 
D． 
12、小王利用计算机设计了一个计算程序，输入和输出的数据如下表：
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … |
|
|
|
|
| … |
那么，当输入数据为8时，输出的数据为（ ）
A. 
B. 
C.
D. 
二.填空：（每小题3分，共24分）
1.若 
，则 
。
2.最简根式
和
是同类根式，则a=__________，b=__________．
3.AB是⊙O直径，AB=4，F是OB中点，弦CD⊥AB于F，则CD=_________
4.如图所示，下列各图中， 绕一点旋转1800后能与原来位置重合。
 | |||
 | |||
5..如图，AB是⊙O的直径，弦CD垂直平分OB，则∠BDC=__________ （5题）
6.△ABC内接于⊙O，∠ACB＝36°，那么∠AOB的度数为__________
7.三角形两边长分别为3和6，第三边是方程
的解，则这个三角形的周长是___。
8.口袋中放有3只红球和11只黄球，这两种球除颜色外没有任何区别，随机从口袋中任取一只球，取得黄球的概率是_________．
9．已知一条弧的长是3
厘米, 弧的半径是6厘米,则这条弧所对的圆心角是 度.
三、解答题：（每小题4分，共24分）
1.、解下列方程：
（1）
（2）
（3）解方程 (x-3)2 +2x(x-3)＝0
2.计算题：
（1）．
（2）． 
（3）计算：．
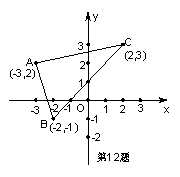
3.、如图，画出△ABC关于原点O对称的△A1B1C1，并求出点A1，B1，C1的坐标。
 |
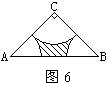
四、(本题7分) 如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆。
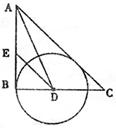求证：（1）AC是⊙D的切线；
（2）AB+EB=AC。
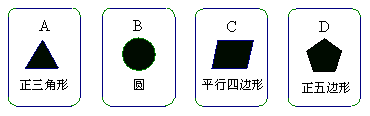
五．有四张背面相同的纸牌A、B、C、D，其正面分别画有四个不同的几何图形（如图），小华将这四张牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．
（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；
（2）求摸出两张牌面图形都是中心对称图形的纸牌的概率．
 |
25、（14分）某地区为了加大“退耕还林”的力度，出台了一系列的激励措施：在“退耕还林”过程中，每一年的林地面积达到10亩且每年的林地面积在增加的农户，当年都可得生活补贴费2000元，且每超过10亩的部分还给予奖励每亩a元，在林间还有套种其他农作物，平均每亩还有b元的收入。下表是某农户在头两年通过“退耕还林”每年获得的总收入情况：
| 年份 | 拥有林地的亩数 | 年总收入 |
| 2002 | 20 | 3100元 |
| 2003 | 26 | 5560元 |
（注：年总收入＝生活补贴量+政府奖励量＋种农作物收入）
（1） 试根据以上提供的资料确定a、b的值。
（2） 从2003年起，如果该农户每年新增林地的亩数比前一年按相同的增长率增长，那么2005年该农户获得的总收入达到多少元？