九年级上学期数学期中测试卷

九年级上学期数学期中测试卷

(时间:120分钟,　满分:120分)

命题人:陈健　　审核人:张召谷　　　　　　　　　　　　　　　　　　　　　　  分数:

一、选择题.(12×3分=36分)

1、要使二次根式有意义，那么x的取值范围是（　　）

（A）x＞－1　 （B） x＜1　　　（C） x≥1　　　 （D）x≤1

2、 在下面4个图案中，中心对称图形为(　　)

3、下列二次根式中，最简二次根式是（　　 ）

　(A)．　　 (B)．　　(C)．　　(D)．

4、下列一元二次方程有两个相等实数根的是(　　)

 (A)．x²-x+1=0 (B)．2x²-3x-1=0　(C)．x²-6x+9=0　(D)．X²-4x+2=0

5、如图,圆心角∠AOB=80°,则圆周角∠ACB的度数为(　　)

（A）80°　 （B） 40°　　 （C） 60°　　（D）45°

6、正八边形绕它的中心旋转后与原图形重合,旋转角的最小值为(　　)

（A）180°　 （B） 135°　　 （C） 60°　　（D）45°

7、已知⊙O₁与⊙O₂的圆心距O₁O₂＝6cm，且两圆的半径满足一元二次方程x²-6x+8=0，则两圆的位置关系为　(　　)

(A)．外切　　　(B)．内切　　　(C)．外离　　　(D)．相交

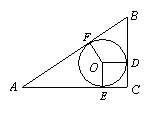
8、如图，在△ABC中，已知∠C=90°，BC=3，AC=4，

则它的内切圆半径是（　　）

(8题)

(A)．　　　 (B)．　　  (C)．2　　　　(D)．1

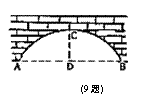
9、如图，圆弧形桥拱的跨度AB＝12米，拱高CD＝4米，则拱桥的半径为（　　　　）

(A)　6.5米　  (B) 9米　　(C) 13米　　 (D)　15米

10、某省2006年全年对外贸易总额为16.5亿元,近5年对外贸易

总额年平均增长率为10.8﹪,下列说法:①2005年该省对外贸易总

为16.5(1-10.8﹪)亿元,②2005年该省对外贸易总为16.5÷(1+

10.8﹪)亿元,③预计2008年该省对外贸易总为16.5(1+10.8﹪)²

亿元,④预计200年该省对外贸易总为16.5÷(1-10.8﹪)²亿元.

其中正确的说法有(　　)

(A)①③　  (B) ①④　 (C) ②③　 (D)　②④

11、已知弧AB和弧CD是⊙O的两条劣弧,且弧AB=2×弧CD,则弦AB和CD的大小关系是(　　)

(A)　AB=2CD　　(B) AB＞2CD　 (C) AB＜2CD　  (D)　以上答案都不对

12、如图,AB是⊙O的直径，M是⊙O上一点，MN⊥AB，垂足为N，P、Q分别是弧AM、弧BM上一点（不与端点重合）,已知∠MNP=∠MNQ，　　下面结论: ①∠1=∠2；　　②∠Q=∠PMN；③∠P+∠Q=180°；④PM=QM；⑤MN²=PN·QN。

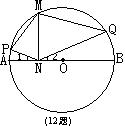其中正确的个数有（　）

(A)．1个　　(B)．2个　　(C)．3个   (D)．4个

二、填空题(4×3分=12分)

13、关于x的一元二次方程(a-1)x²+x+a²-1=0的一个根为0,

则a=　　　　 。

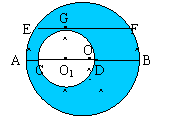14、如图,大⊙O与小⊙O₁的连心线OO₁分别交两圆于A、C、

D、B, ⊙O的弦EF与⊙O₁相切于G,且EF∥AB,EF=8㎝,图中

阴影部分的面积为:　　　　　 .

15、△ABC内接于半径为2㎝的⊙O,且AB=2㎝,

则∠ACB=　　　　　  .

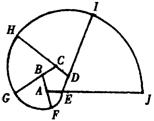
16、如图，五边形ABCDE是正五边形，曲线EFGHIJ……叫

做“正五边形 ABCDE的开线”，其中弧线EF、FG、GH、HI、

IJ…的圆心依次按A、B、C、D、E循环，它们依次相连接．如

果AB＝1，那么曲线 EFGHIJ的长度为　　　　　　 .

三、解答题(3×6分=18分)

17解方程:x²-2x-2=0　　　　　 18、计算:

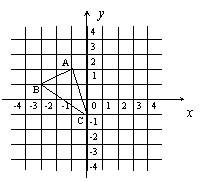19、如图，若将△ABC的绕点C顺时针旋转90°后得

到△DEC，则A点的对应点D的坐标是　　　　,B点

的对应点E的坐标是　　　　,请画出旋转后的△DEC

(不要求写画法)

四、解答题(2×7分=14分)

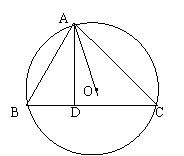20、如图,△ABC内接于⊙O,AD⊥BC于点D,

求证:∠BAD=∠CAO

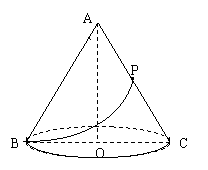21、如图,有一圆椎形粮堆高为2m,母线AB=4m,母线AC的中点处有一老鼠正在偷吃粮食,小猫从B处沿圆椎表面去偷袭老鼠,求小猫所经过的最短路程是多少?

五、解答题(2×9分=18分)

22、某公司经销一种绿茶，每千克成本50元，物价部门规定这种绿茶的销售单价不得高于90元/千克，市场调查发现在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：w＝-2x+240.解答下列问题：

(1)公司要想这段时间内获得2250元的销售利润，销售单价应定为多少元？

(2)当销售单价定为多少元/千克时利润最大?最大利润是多少?

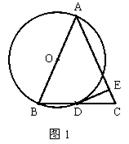
23. 已知: 如图，点O在等腰△ABC的一腰AB上.

⑴若AB为⊙O的直径，⊙O交BC于D，过D作DE⊥AC于E.

求证:DE是⊙O的切线.

⑵如果点O由⑴中的位置在AB上向点B移动，以O为圆心，

以OB长为半径的圆交BC于D，若S_△ABC=25,AB=10,点O移动

到何处⊙O与AC相切于点F?

六、解答题(10分)

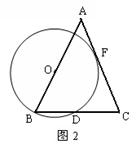
24.如图，已知正方形ABCD的各边中点分别为E、F、G、H.

图①

点M为直线BC上一动点,以线段EM为边长作正方形EMNP.

(1)如图①,当M点在点B的左侧时,请你判断FM和HP有何

数量关系?点P是否在直线FH上?

(2)如图②, 当M点在BC边上时,请你判断FM和HP有何数

图②

量关系?点P是否在直线FH上?

(3)如图③, 当M点在点C的右侧时,请你判断FM和HP有

何数量关系?点P是否在直线FH上?

请分别写出各小题的结论,并从三小题中任选一题证明你的

结论.

七、综合题(12分)

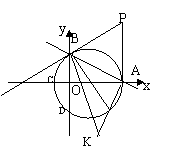25、如图,直线y=-x+4交x轴A,交y轴于B,M为OA上一点,⊙M经过B、A两点,交x轴负半轴于一点C,交y轴的负半轴于一点D.

(1)求M的坐标.

(2)BM的延长线交⊙M于E,直线BA绕B点顺时针旋转经过

M

△OBM的内心I时交AE的延长线于K,求线段AK的长.

E

(3)分别过A、B两点作⊙M的切线相交于点P,过AB两点的

动圆⊙N交PB的延长线于G,交y轴的负半轴于H.有两个

结论:①BH+BG的值不变,②BH-BG的值不变.其中只有一个

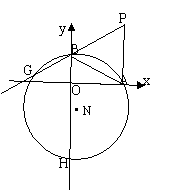是正确的.请作出判断,并求其值.