九年级数学第一学期第一次月考

九年级数学第一学期第一次月考

数 学 试　题

（时间120分钟　 总分120分）　命题:曹经富

题号	一	二	三	总分
得分

一、认真填一填：（每小题3分，共30分）

1．方程x(x+3)=(x+3)的根为　　　　　　  。

2、若两个最简二次根式与可以合并，则=　　　　。

3、若式子有意义，则x的取值范围为　　　　　　  。

4、已知＜0，则化简二次根式的正确结果是　　　　　　  。

5．已知x²＋4x－2=0，那么3x²＋12x＋2000的值为　　　　　　  。

6、请写出一个根为x= －2的一元二次方程　　　　　　 。

7、关于x的一元二次方程kx²-6x+1=0有两个不相等的实数根,则k 的取值范　　围是　　　 。

8、已知：是整数，则满足条件的最小正整数为　　　　　　 。

9、已知方程的一个根是1，则另一根是　　　　　　  。

m的值是　　　　　　  。

10、下面是按照一定规律画出的一列“树型”图：

　 
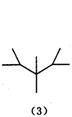
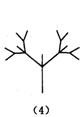
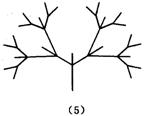
经观察可以发现：图⑵比图⑴多出2个“树枝”，图⑶比图⑵多出5个“树枝”，图⑷比图⑶多出10个“树枝”，照此规律，图⑺比图⑹多出_________个“树枝”．

二、精心选一选：（每小题3分，共24分）

11、下列属于一元二次方程是【　  】

A、　　　　　 B、

C、　　　　　 D、

12、下列方程没有实数根的是-----------------------------------------(　　)

A. x²-x-1=0　　　　B. x²-6x+5=0　　　 C.　　  D.2x²+x+1=0.

13.等腰三角形的底和腰是方程x²-6x+8=0的两根，则这个三角形的周长为--（　　）

A.8　　　　　　  B.10　　　　  C.8或10　　　　D.不能确定

14 式子中，是最简二次根式的式子有（　）个

A、2　　　　　　　 B、3　　　　　　　C、1　　　　　　　D、0

15．下列变形中，正确的是………------------------------------------------（　　）

（A）(2)²＝2×3＝6　　　 （B）＝－

（C）＝　　 （D）＝．

16、下列说法：

①、是二次根式，但不是整式；

②、方程的根为；

③、若＜0，则方程必有两个不相等的实数根；

④、课本第54页观察与猜想讨论了一元二次方程根与系数的关系，根据这一关系得方程的两根和是3，两根积是5。

其中错误的有【　　】

A、3个　　　B、2个　　　C、1个　　　D、0个

17．在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图1所示，如果要使整个挂图的面积是5400cm²，设金色纸边的宽为xcm，那么x满足的方程是（  ）

A．x²+130x-1400=0　　　　B．x²+65x-350=0

C．x²-130x-1400=0　　　　D．x²-65x-350=0

18、根据关于的一元二次方程，可列表如下：

	0	0.5	1	1.1	1.2	1.3
		－8.75	－2	－0.59	0.84	2.29

则方程的正数解是【　　】

A、整数部分是1，十分位是1；　 B、整数部分是1，十分位是2；

C、整数部分是0，十分位是5；　 D、整数部分是0，十分位是8；

三、认真解一解：

19．计算：（每小题3分，共12分）

1.　　　　　　　2、

3、 　　　　　4、

20、用适当方法解下列方程：（3+3+4，共10分）

1)、　　　　　　  2)　 

⑶、 (x+1)²=4(x-2)²

21、（8分）

已知关于x的一元二次方程x²＋4x＋m－1＝0。

(1)请你为m选取一个合适的整数，使得到的方程有两个不相等的实数根；

(2)设x₁、x₂是(1)中你所得到的方程的两个实数根，求：－x₁－x₂＋x₁x₂的值。

22、解应用题：（8分）

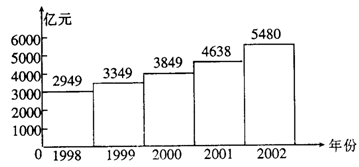
“国运兴衰，系于教育”图中给出了我国从1998─2002年每年教育经费投入的情况．

　　（1）由图可见，1998─2002年的五年内，我国教育经费投入呈现出_______趋势；

　　（2）根据图中所给数据，求我国从1998年到2002年教育经费的年平均数；

　　（3）如果我国的教育经费从2002年的5480亿元，增加到2004年7891亿元，那么这两年的教育经费平均年增长率为多少？（结果精确到0.01，=1.200）

23、（9分）先阅读再化简求值：

（1）在化简的过程中。小张和小李的化简结果不一样：小张的化简过程如下：

原式=

小李的化简过程如下：

原式=

请判断谁的化简结果是正确的，谁的化简结果是错误的，并说明理由？

（2）请你利用上面所学的方法,化简求值：已知，求x²+2x-3的值.

相信你能行（本题9分）

24,　有100米长的篱笆材料，想围成一个矩形露天仓库，要求面积不小于600平方米，在场地的北面有一堵长为50米的旧墙，有人用这个篱笆围成一个长40米，宽10米的矩形仓库，但面积只有400平方米，不合要求，现请你设计三种矩形仓库的长和宽，使它符合要求．

动脑想一想（10分）

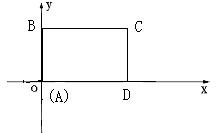
25, 如图所示，在直角坐标系中，矩形ABCD的边AD在x轴上，点A在原点，AB＝3，AD＝5．若矩形以每秒2个单位长度沿x轴正方向作匀速运动．同时点P从A点出发以每秒1个单位长度沿A－B－C－D的路线作匀速运动．当P点运动到D点时停止运动，矩形ABCD也随之停止运动．

（1）求P点从A点运动到D点所需的时间；

（2）设P点运动时间为t（秒）。

①当t＝5时，求出点P的坐标；

②若⊿OAP的面积为s，试求出s与t之间的函数关系式（并写出相应的自变量t的取值范围）．