九年级数学第一学期期中模拟考试
（ 考试时间：90分钟 试卷满分：100分）
一、选择题（本大题共12小题，每小题2分，计24分）
1．函数
中自变量
的取值范围 （ ）
A.
B. 
C.
D.
2．若a<1，化简
的结果是 （ ）
A、a－1 B、－a－1 C、1－a D、a+1
3．一元二次方程
的解是 （ ）
Ａ．
，
Ｂ．
，
Ｃ．
，
Ｄ．
，
4．下列关于
的一元二次方程中，有两个不相等的实数根的方程是（ ）
A.
B.
C.
D.
5．等腰三角形的一个底角为
，则它的顶角为 （ ）
A.
B.
C.
D.
6．下列图形中，即是中心对称图形又是轴对称图形的是 （ ）
A．等边三角形 B．菱形 C．等腰梯形 D．平行四边形
7．梯形的上底长为
，下底长是上底长的3倍，则该梯形的中位线长为 （ ）
A. B.1.5
C.2
D.4
8．刘翔为了备战2008年奥运会，刻苦进行110米跨栏训练，为判断他的成绩是否稳定，教练对他10次的成绩进行统计分析，教练需要了解刘翔这10次成绩的 （ ）
A．众数 B．方差 C．平均数 D．频数
9．如果等边三角形的边长为3，那么连结各边中点所成的三角形的周长（ ）
A．9
B．6
C．3
D．
10. 下列说法中错误的是（ ）
（A）一组对边平行且一组对角相等的四边形是平行四边行
（B）每组邻边都相等的四边形是菱形
（C）四个角相等的四边形是矩形
（D）对角线互相垂直的平行四边形是正方形
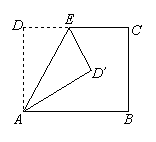11．如图，将矩形ABCD沿AE折叠，若∠BAD′＝30°，则∠AED′ 等于
（ ）
A．30° B．45° C．60° D．75°
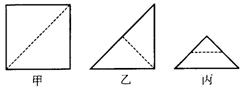
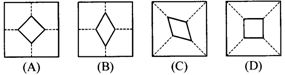
12．小许拿了一张正方形的纸片如图甲，沿虚线对折一次得图乙．再对折一次得丙．然后用剪刀沿图丙中的虚线（虚线与底边平行）剪去一个角．打开后的形状是 （ ）．
二、填空题（本大题共8小题，每小题2分，计16分）
13．计算：
。
14、已知(m+3)x2-3mx-1=0是一元二次方程，则m的取值范围是
15、在四边形ABCD中，已知AB∥CD，请补充一个条件： ，使得四边形ABCD是平行四边形。
16．方程
的解是
。
17、已知xy＜0，
化简后为
。
18．有一组数据11，8，10，9，12的极差是______，方差是_________。
19．已知矩形的面积为
，一边长为
，那么另一边长为
。
20．已知菱形的两条对角线长分别为
和
，则该菱形的面积
。
三、解答题（本大题共5小题，计42分）
21．计算：（本题共2小题，每小题4分，计8分）
（1）
（2）
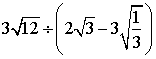
22．解方程：（本题共2小题，每小题5分，计10分）
（1）
（2）
23．（本小题8分）
某厂2004年的产值为2000万元，2006年产值为2420万元，假设此厂每年产值增长率相同，那么2004到2006年产值的年平均增长率是多少？
24．（本小题8分）已知：如图，AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F.求证：AD⊥EF.
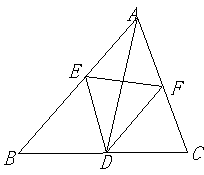
25.（本小题8分）
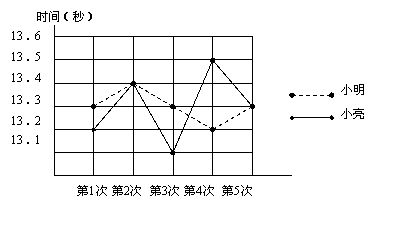
为了让广大青少年学生走向操场、走进自然、走到阳光下，积极参加体育锻炼，我国启动了“全国亿万学生阳光体育运动”．短跑运动，可以锻炼人的灵活性，增强人的爆发力，因此小明和小亮在课外活动中，报名参加了短跑训练小组．在近几次百米训练中，所测成绩如图所示，请根据图中所示解答以下问题．
（1）请根据图中信息，补齐下面的表格；
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 小明 | 13.3 | 13.4 | 13.3 | 13.3 | |
| 小亮 | 13.2 | 13.1 | 13.5 | 13.3 |
（2）从图中看，小明与小亮哪次的成绩最好？
（3）分别计算他们的平均数、极差和方差，若你是他们的教练，将小明与小亮的成绩比较后，你将分别给予他们怎样的建议？
 |
四、操作题（本小题8分）
26、如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是
60°），菱形
的边长为2，E是
的中点，按
将菱形剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．
（1）在下面的菱形斜网格中画出示意图；
（2）所拼成的三种图形的外围周长分别为 l1 ,l2 ,l3的大小关系（用“=”、“＞”或“＜”连接）： 周长关系是 ．
五．探究题（本小题满分10分）
27、已知，如图□ABCD中，AB⊥AC，AB=1，BC=
，对角线AC、BD交于0点，将直线AC绕点0顺时针旋转，分别交BC、AD于点E、F
⑴、 证明：当旋转角为90°时，四边形ABEF是平行四边形；
⑵、试说明在旋转过程中，线段AF与EC总保持相等；
⑶、在旋转过程中，四边形BEDF可能是菱形吗?如果不能，请说明理由；如果能，
说明理由并求出此时AC绕点0顺时针旋转的度数。
