九年级数学第一学期月考试题
命题人： 审核人： 校对人：
说明：1.全卷共3大题，共6页，考试时间90分钟，满分100分。
2.答题前，请将考场、试室号、座位号、考生号和姓名写在试卷密封线内，不得在试卷上做任何标记。
3.答选择题时，请将选项的字母写在答题表一内，填空题的答案写在答题表二中，否则不给分。
| 题号 | 一 | 二 | 三 | ||||||
| 1—10 | 11—15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | |
| 得分 | |||||||||
| 复核人 | |||||||||
| 得分 | 阅卷人 |
|
|
|
一、选择题（本大题共10小题，每小题3分，共30分）
每小题给出４个答案，其中只有一个是正确的．请把正确答案的代号，填入答题表一中，否则不给分.
答题表一
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1．方程x2－1＝0的根是（ ）
A．x＝1 B．x＝0 C．x1＝1，x2＝0 D．x1＝1，x2＝－1
2．用配方法解方程x2+8x+7=0,则方程可变为（ ）
A．（x－4）2＝9 B．(x＋4)2＝9 C．(x－8)2＝16 D．(x＋8)2＝57
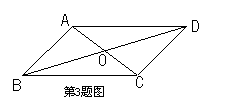3．如图所示，在平行四边形ABCD中，对角线AC、BD交于点O，下列式子中一定成立的是 ( )
A．AC⊥BD B．OA=OC C．AC=BD D．AO=OD
4．把下列方程化成一般形式后，系数和为0的方程是（ ）
A．x2－2x＋3＝0 B．x2＋2x－3＝0
C．x2－4x－3＝0 D．2x2－5＝3x
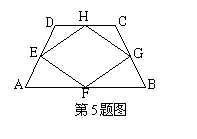
5．如图所示，在梯形ABCD中，AB∥CD，AD=BC，点E、
F、G、H分别是梯形各边的中点，则四边形EFGH一定是
A．菱形 Ｂ．矩形 Ｃ．正方形 Ｄ．等腰梯形
6．下列四个命题中，是假命题的是（ ）.
A． 四条边都相等的四边形是菱形；
B．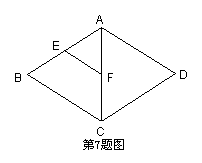 
有三个角是直角的四边形是矩形；
C．对角线互相垂直平分且相等的四边形是正方形；
D．一组对边平行，另一组对边相等的四边形是等腰梯形.
7．如图，在菱形ABCD中，E，F分别是AB，AC的中点，如果EF=2，那么菱形ABCD的周长是（ ）
A．4 B．8 C．12 D．16
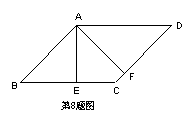8．如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，∠EAF=45o，且AE+AF=
，则平行四边形ABCD的周长是 （
）
A．4 B．8 C．12 D．16
9．某城市2003年底已有绿化面积300公顷，经过两年绿化，绿化面积逐年增加，到2005年底增加到363公顷．设绿化面积平均每年的增长率为x，由题意，所列方程正确的是（ ）
A．300(1＋x)=363 B．300(1＋x)2=363
C．300(1＋2x)=363 D．363(1－x)2=300
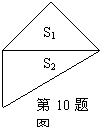
10.将一副三角板如图所示的放置，有两条边恰好完全重合，则上
下两块三角板的面积之比
:
A．
: 2 B．: 3 C．3 : D．2 :
| 得分 | 阅卷人 |
|
|
|
二、填空题(本大题共5小题，每小题3分，共15分)
请将答案填在答题表二内相应的题号下，否则不给分．
| 答题表二 | |||||
| 题 号 | 11 | 12 | 13 | 14 | 15 |
| 答 案 | |||||
|
11．已知方程3x2－9x＋m＝0的一个根是1，则m的值为
|
|
|
 |
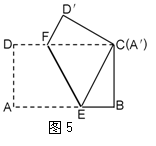15．．如图所示，将矩形ABCD沿EF折叠，使得点Ａ恰与
点Ｃ重合．折叠后测得∠BCE = 30°，BE＝2cm，那么
折痕EF = 
cm.
三、解答题（本大题有7题，其中第16、17题各6分；第18题７分；第19、20题各８分；第21、22题各10分，共55分）
| 得分 | 阅卷人 |
|
|
|
16．（6分）解方程：
17．（6分）解方程：3x(x－1)＝2－2x
| 得分 | 阅卷人 |
|
|
|
18．（7分）已知：如图，在平行四边形ABCD中，E、F分别是AB、CD的中点。
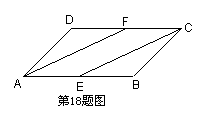求证：（1）△AFD≌△CEB。
（2）四边形AECF是平行四边形。
| 得分 | 阅卷人 |
|
|
|
19（8分）先阅读下面题目及某同学给出的证明，再根据要求回答问题.
已知，如图，在平行四边形ABCD中， ∠BAD的平分线与BC边相交与点E，∠ABC的平分线与AD边相交与点F，AE与BF相交与点O.
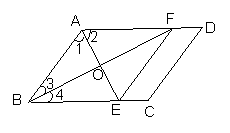求证：四边形ABEF是菱形.
证明：①∵四边形ABCD是平行四边形；
②∴AD∥BC；
③∴∠ABE+∠BAF=180°
④∵AE、BF分别是∠BAF、∠ABE平分线；
⑤∴∠1=∠2=
∠BAF，∠3=∠4=∠ABE；
⑥∴∠1+∠3=（∠BAF+∠ABE）=×180°=90°；
⑦∴∠AOB=90°
⑧∴AE⊥BF；
⑨∴四边形ABEF是菱形.
问：（1）上述证明是否正确？
（2）如有错误，指出在第 步到第 步推理错误，应在第 步后添加以下证明过程：
| 得分 | 阅卷人 |
|
|
|
20．（8分）某西瓜经营户以2元/千克的价格购进一批小型西瓜，以3元/千克的价格出售，每天可售出200千克。为了促销，该经营户决定降价销售。经调查发现，这种小型西瓜每降价0.1元/千克，每天可多售出40千克。另外，每天的房租等固定成本共24元。该经营户要想每天盈利200元，应将每千克小型西瓜的售价降低多少元？
21．(10分)在△ABC中，∠B=22.5°，∠C=30°，AB的垂直平分线OD交BC边于点D，连结AD
(1)
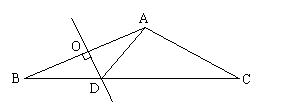求∠DAC的度数
(2) 若AC=4cm，求△ABC的面积(结果保留根号)
| 得分 | 阅卷人 |
|
|
|
22．（10分）如图，在梯形ABCD中，AB∥CD，∠BCD=90°, 且AB、BC的长是方程
x2－3x＋2＝0的两个根（AB＜BC），AD=
.
(1)
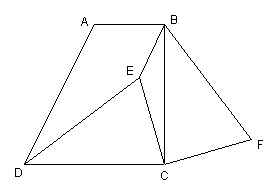（3分）求证：DC=BC;
(2) （3分）E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断
CE、CF的数量关系，并证明你的结论；
(3) （4分）在（2）的条件下，当BE：CE=1：2，BE=a，∠BEC=135°时，求DE的长.