§3.2一次函数
复习目标
1．一次函数：若两个变量x、y间的关系式可以表示成y=kx＋b(k、b为常数，k ≠0）的形式，则称y是x的一次函数；特别地，当b=0时，称y是x的正比例函数．
2．一次函数的图象：一次函数y=kx+b的图象是经过点(0，b),(－，0 ）的一条直线，正比例函数y=kx的图象是经过原点(0，0）的一条直线，如下表所示．
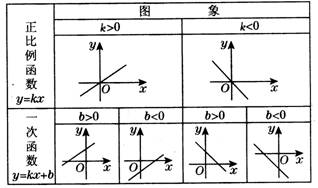
3．一次函数的性质：y=kx＋b(k、b为常数，k ≠0）当k ＞0时，y的值随x的值增大而增大；当k＜0时，y的值随x值的增大而减小．
4．直线y=kx＋b(k、b为常数，k ≠0）时在坐标平面内的位置与k在的关系．
⑴
直线经过第一、二、三象限（直线不经过第四象限）；
⑵
直线经过第一、三、四象限（直线不经过第二象限）；
⑶
直线经过第一、二、四象限（直线不经过第三象限）；
⑷
直线经过第二、三、四象限（直线不经过第一象限）。
5．一次函数表达式的求法：确定一次函数表达式常用待定系数法，其中确定正比例函数表达式，只需一对x与y的值，确定一次函数表达式，需要两对x与y的值。
典例精析
【例1】若函数
是一次函数，求
的值，并写出解析式。
【分析】本题需注意两个方面，①
的次数为1②的系数不等于零。
【解答】由题意得，
，则
，
因为
，所以
则 
所以它的解析式为
【例2】（2006遂宁）地表以下岩层的温度t(0C)随时着所处的深度h(千米)的变化而变化, t与h在一定范围内近似成一次函数关系
(1)根据下表,求t(0C)与 h(千米)之间的函数关系式;
(2)求当岩层温度达到7700C时,岩层所处的深度为多少千米?
| 温t(0C) | ··· | 90 | 110 | 300 | ··· |
| 深度h(千米) | ··· | 2 | 4 | 8 | ··· |
【分析】本题用待定系数法确定一次函数的关系式。
【解答】⑴设
，选取两组值代入可得方程组：
解得
，所以所求的函数关系式
⑵当
。
所以当岩层温度达到7700C时,岩层所处的深度为70千米。
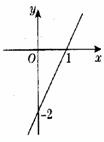
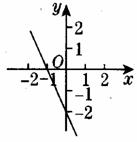
【例3】已知一次函数y=kx+b的图象如图所示，当x＜0时，y的取值范围是（ ）
A．y＞0 B、y＜0
C、－2＜y＜0 D．y＜－2
【分析】由图象可知一次函数y=kx＋b过一、三、四象限，当x＜0时，y对应的值在－2的下方．故 选D
【解答】D
【例4】已知一次函数
，试讨论其图像经过哪些象限？
【分析】由
的正负性，分情况画出草图，进而判断直线所经过的象限．
【解答】（1）当
时，可得
，
由图（1）知函数图像经过第一、二、四象限．
（1）
（2）当
时，可得，
由图（2）知，函数图像经过第一、二、三象限．
（2）
（3）当
时，函数为
，
由图（3）知，函数图像经过一、三象限．
（3）
（4）当
时，可得
，
由图（4）知，函数图像经过第一、三、四象限．
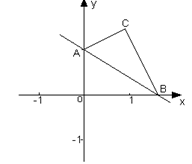
【例5】（2006旅顺）直线
分别与轴、
轴
交于B、A两点．
⑴求B、A两点的坐标；
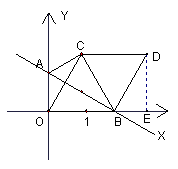⑵把△AOB以直线AB为轴翻折，点O落在平面上的点C处，以BC为一边作等边△BCD。求D点的坐标．
【分析】本题把一次函数的知识与三角形结合在一起。
【解答】（1）B、A两点的坐标分别为
。
（2）如图，在
；则
。
①若以BC为一边向左下方作等边△BCD，则D点刚好与原点O重合，此时D点的坐标为（0，0）。
②若以BC为一边向右上方作等边△BCD，过D点作
。由已知可得在
则此时D点的坐标为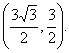
课内巩固
l．下列关于x的函数中，是一次函数的是（ ）
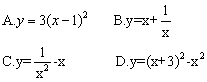
2．如果直线y=kx+b经过一、二、四象限，那么有（ ）
A．k＞0，b＞0 B．k＞0，b＜0
C．k < 0，b＜0 D．k ＜0，b＞0
3．油箱中存油20升，油从油箱中均匀流出，流速为0．2升／分钟，则油箱中剩余油量 Q（升）与流出时间t(分钟）的函数关系是（ ）
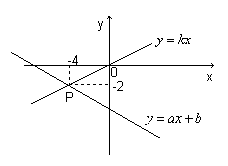A．Q＝0．2t
B．Q＝20－0.2t
C．t=0．2Q D．t=20—0．2Q
4．（2006北京）如果正比例函数的图象经过点(1，2)，那么这个正比例函数的解析式为 。
5．已知一次函数y=kx+2，请你补充一个条件______，使y随x的增大而减小．
6．（2006重庆）如图，已知函数
和
的图象交于点P, 则根据图象可得，关于
的二元一次方程组的解是
7．（2006河北）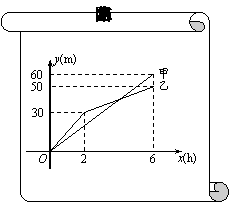
甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度y（m）与挖掘时间x（h）之间的关系如图所示，请根据图象所提供的信息解答下列问题：
（1）乙队开挖到30m时，用了_____h．开挖6h
时甲队比乙队多挖了_____m；
（2）请你求出：
①甲队在0≤x≤6的时段内，y与x之间的函
数关系式；
②乙队在2≤x≤6的时段内，y与x之间的函数关系式；
（3）当x为何值时，甲、乙两队在施工过程中所挖河渠的长度相等？
8.（2006大连）在围棋盒中有x颗黑色棋子和y颗白色棋子，从盒中随机地取出一个棋子，如果它是黑色棋子的概率是
。
（1）试写出y与x的函数关系式。www.1230.org 初中数学资源网
（2）若往盒中再放进10颗黑色棋子，则取得黑色棋子的概率变为
，求x和y的值。
课外拓展
A组
1. 在下列函数中，满足x是自变量，y是因变量，b是不等于0的常数，且
是一次函数的是（ ）
2．直线y=2x+6与x轴交点的坐标是（ ）
A．（0，－3）B．（0，3）C．（3，0）D.（－3,0）
3．（2006北京）一次函数y=x+3的图象不经过的象限是（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
4．直线 y=x＋4与 x轴交于 A，与y轴交于B, O为原点，则△AOB的面积为（ ）
A．12 B．24 C．6 D．10
5．一次函数的图象如图所示，那么这个一次函数的表达式是（ ）
A．y＝－2x＋2 B．y＝－2x－2
C．y＝ 2x＋2 D．y＝2x－2
6．已知方程组
的解为
，则一次函数y=2x+3与
y= x+的交点坐标为（ ）
A．（l，5）B．（－1，1）C．（l，2）D．（4，l）
7．若一次函数y=kx—3经过点(3，0)，则k=______，该图象还经过点( 0， ）
和（______，－2）。
8. （2005湖州市）在正常情况下，一个人在运动时所能承受的每分钟心跳的最高次数S（次/分）是这个人年龄n（岁）的一次函数。
（1）根据以下信息，求在正常情况下，S关于n的函数关系式；
（2）若一位63岁的人在跑步，医生在途中给他测得10秒心跳为26次，问：他是否有危险？为什么？
9．某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用后，那么服药后2小时血液中含药量最高，达每毫升6微克，（1微克＝10－3毫克），接着逐步衰减，10小时时血液中含量为每毫升3微克，每毫升血液中含药量（微克）随时间（小时）的变化如图所示。当成人按规定剂量服用后：
（1）分别求出≤2和≥2时与之间的函数关系式；
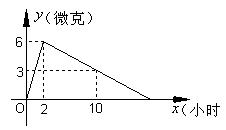（2）如果每毫升血液中含药量为4微克或4微克以上时，在治疗疾病时是有效的，那么这个有效的时间是多长？
B组
10．一次函数y=2x＋4的图象如图所示，根据图象可知，当x_____时，y＞0．
11．如图，直线y=2x—l关于x轴成轴对称的图形的表达式 。
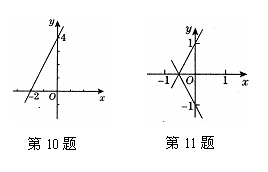
12．（2006黄冈）如图，在光明中学学生耐力测试比赛中，甲、乙两学生测试的路程S(米)与时间t(秒)之间的函数关系图像分别为折线OABC和线段OD，下列说法正确的是（ ）
A、乙比甲先到达终点
B、乙测试的速度随时间增加而增大
C、比赛进行到29.4秒时，两人出发后第一次相遇
D、比赛全程甲的测试速度始终比乙的测试速度快
 |
13．一次函数 y=kx＋b，当－3≤x≤1时，对应的y值为1≤y≤9，则k·b的值为（ ）
A．14 B．－6 C．－4或 21 D．－6或 14
14．（2006年襄樊）汉江市政府为响应党中央建设社会主义新农村和节约型社会的号召,决定资助部分农村地区修建一批沼气池,使农民用到经济、环保的沼气能源。红星村共有360户村民，村里得到34万元的政府资助款，准备再从各户筹集一部分资金修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用的户数、修建用地情况见下表：
| 沼气池 | 修建费用（万元/个） | 可供使用户数（户/个） | 占地面积（m2/个） |
| A型 | 3 | 20 | 10 |
| B型 | 2 | 15 | 8 |
政府土地部门只批给该材沼气池修建用地188m2,若修建A型沼气池x个，修建两种沼气共需费用y万元。
（1）求y与x之间的函数关系式；
（2）试问有几种满足经上要求的修建方案？
（3）平均每户村民筹集500元钱，能否满足所需费用最少的修建方案。
15．（2006徐州）（1）在图1所示的平面直角坐标系画出点A（2，3），再画出点A关于轴的对称点
，则点的坐标为
。
（2）在图1中画出过点A和原点O的直线
，则直线的函数关系式为
；再画出直线关于轴的对称的直线
，则直线的函数关系式为
。
（3）在图2所示的平面直角坐标系画出直线
，再画出直线关于轴的对称的直线
，则直线的函数关系式为
。
（4）请你根据自己在解决以上问题的过程中所获得的经验回答：直线
关于轴对称的直线的函数关系式为
。
图1 图2
反思纠错
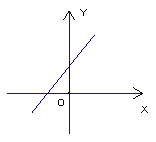
1．函数
的图象不通过第四象限，则（ ）
解：函数的图象不通过第四象限，即如图：
则可得：
，因此选A。
这样做对吗？为什么？
2．已知函数的图象经过点（0，-4）且与两坐标轴所围成的三角形的面积为8，求它的解析式。
解：
请指出上述解法的错误，并给予更正。