九年级数学卷月练2试题

九年级数学卷月练2试题

（满分：150分　　时间：120分钟）

制卷人：吴克明

一. 填空题:( 本题共10小题，每题4分，共40分)

1．已知＝4，＝9，是的比例中项，则＝　　　　．

2．已知：x∶y∶z=2∶3∶4，则的值为　　　　　 。

3．在比例尺为1：10000的地图上，皖西中学的周长为18cm，则实际周长为　　　　　 。

4. 小明身高是1.6m，影长为2m，同时刻教学楼的影长为24m，则楼的高是　　　　   。

5．若△ABC∽△A′B′C′，且，△ABC的周长为12cm，则△A′B′C′的周长为　　　　 。

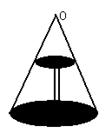
6．如图，这是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地上形成阴影（圆形 ）的示意图，已知桌面的直径为1.2米，桌面距地面1米，灯泡距地面3米，则地上阴影部分的面积是______.　　　　　　 

7. 如图中，有三个正方形，，，则第三个正方形的边长　　　　．

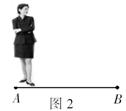
8. 如图节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体，若舞台长为20m，主持人应走到离点　　　　　　　　　  处？ (结果保留根号)

9. 在△ABC中，∠B＝38°，AD是BC边上的高，并且，则∠BCA的度数为__________．

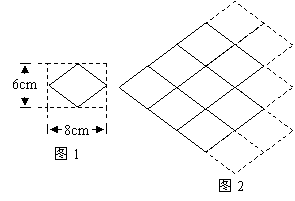
10. 要拼出和图1中的菱形相似的较长对角线为的大菱形（如图2所示），需要图1中的菱形的个数为____________．

二. 选择题: (共40分)

1. 两个相似多边形的面积之比为1∶3，则它们周长之比为　　　　　　　　 （　　　）

A．1∶3　　　B．1∶9　　　　C．1∶　　　　D．2∶3　　

2. 下列说法中不正确的是　　　　　　　　　　　　　　 （　　 ）

　A．有一个角是30°的两个等腰三角形相似；B．有一个角是60°的两个等腰三角形相似；

　C．有一个角是90°的两个等腰三角形相似；D．有一个角是120°的两个等腰三角形相似；

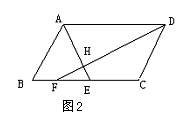3. 如图2，E是平行四边形ABCD的边BC的中点，F是BE的中点，AE与DF相交于H,则FH：DH值为　　　　　　  （　　 ）　

A、　　 B、　　  C、　　　　D、

4. 某校有两块相似的多边形草坪，其面积比为9∶4，其中一块草坪的周长是36米，则另一块草坪的周长是多少米　　　　　  （　　 ）

A、16或81　　 　 B、54　　　 C、81　　 　　D、24或54

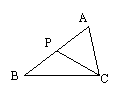
5．如图，若P为△ABC的边AB上一点（AB>AC），则下列条件不一定能保证△ACP∽△ABC的有　　　　　　　　　　　　　　　　 （　　 ）

 A、∠ACP=∠B　 B、∠APC=∠ACB　 C、　　　D、

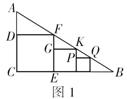
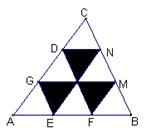
6. 如图，在ΔABC中，AB=30，BC=24，CA=27，　AE=EF=FB，EG∥FD∥BC，FM∥EN∥AC，则图中阴影部分的三个三角形的周长之和为　（　　 ）　　　　

A、70　　　　 B、75　　　　C、81　　 　　D、80

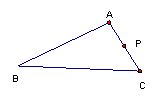7、如图所示，在△ABC中，AB=6，AC=4，P是AC的中点，过P点的直线交AB于点Q，若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似，则AQ的长为　　　　　 　　　　　　　（　　 ）

A、3　　　　　　　B、3或　　  C、3或　　　　　　　 D、

8．△ABC的周长为16，连接△ABC三边的中点构成第一个三角形，再连接这个新三角形的各边中点构成第二个三角形，依次类推，则第2007个三角形的周长为　　　　　　　　　　　  （　　　）

A、　　　 B、　　　　C、　　　　  D、

9. 如图1，扇子的圆心角为xº，余下扇形的圆心角是yº，x与y的比通常按黄金比来设计，这样的扇子外形较美观。若取黄金比为0.6，则x为　　　　　　　　　　　　　　　　　　　　　  （　　　）

　A．216　　 　B．135　　　　C．120　 　　D．108

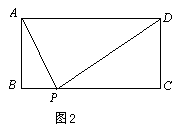
10、如图，矩形ABCD，AD=a，AB=b，要使BC边上至少存在一点P，使△ABP、△APD、△CDP两两相似，则a，b间的关系一定满足　　　　　　　　　　　　　　　　　　　 

（　　　）

A、a≥b　 B．a≥b　 C. a≥b　  D．a≥2b

三.解答题:(共计70分)

1. （本题8分）请作出五边形ABCDE以点O为位似中心的位似图形，使得像和原图形的位似比是1：2。

2. （本题10分）已知x=，求的值。

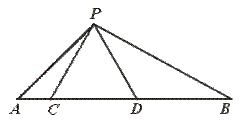
3. （本题10分） 如图，点C、D在线段AB上，⊿PCD是等边三角形．

（1）当AC、CD、DB满足怎样的关系时，⊿ACP∽⊿PDB？

（2）当⊿ACP∽⊿PDB时，求⊿APB的度数．

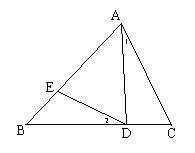
4．（本题10分）已知:如图,ΔABC中,AD=DB,­­∠1=∠2.求证:ΔABC∽ΔEAD.­

　　　　　　　　　　 

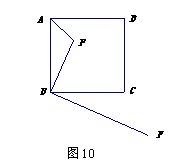
5. （本题10分） 如图，已知点是边长为4的正方形内一点，且，，垂足是．请在射线上找一点（即求出此时BM长），使以点、、为顶点的三角形与相似(请注意：全等图形是相似图形的特例) ．

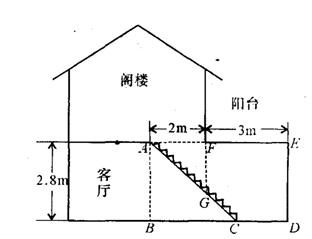
6. （本题10分） 汪老师要装修自己带阁楼的新居（右图为新居剖面图），在建造客厅到阁楼的楼梯 AC 时，为避免上楼时墙角F碰头，设计墙角 F 到楼梯的竖直距离 FG为 1 . 75m ．他量得客厅高 AB = 2 . 8m，楼梯洞口宽AF=2m., 阁楼阳台宽 EF = 3m ．请你帮助汪老师解决下列问题：

第18题图

（1）要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是多少米？

（2）在（1）的条件下，为保证上楼时的舒适感，楼梯的每个台阶小于 20cm，每个台阶宽要大于20cm, 问汪老师应该将楼梯建儿个台阶？为什么？

 

7、（本题12分）如图，已知过A（2，4）分别作x轴、y轴的垂线，垂足分别为M、N，若点P从O点出发，沿OM作匀速运动，1分钟可到达M点，点Q从M点出发，沿MA作匀速运动，1分钟可到达A点。

（1）经过多少时间，线段PQ的长度为2？

（2）写出线段PQ长度的平方y与时间t之间的函数关系式和t的取值范围；

（3）是否存在时间t，使P、Q、M构成的三角形与△MON相似？若存在，求出此时间t；若不可能，请说明理由；

　　　　y

　  N　　　　　　  A

　　　　　　　　   Q

　　 O　　 P　　 M　　　x