九年级数学秋季学期期末测试试题
(本试卷满分120分，考试时间120分钟)
一．选择题：(本题共有8个小题，每小题3分，满分24分)
在下列各小题中，均给出四个答案，其中有且只有一个正确答案，请将正确答案的字母代号填入上面选择题答题表中相应题号下的方格内，填错或不填均为零分。
01．关于x的方程ax2+bx+c=0是一元二次方程的条件是（ ）。
A、a、b、c为任意实数 B、a、b不同时为零
C、a取不为零的实数 D、a取大于零的实数
02．每当晴天，小亮在早晨上学的路上和下午放晚学的路上，面朝前走时，都看不到自己的影子，那么小亮的家在学校的（ ）。
A、东面 B、西面 C、南面 D、北面
03．下列命题中不正确的是（ ）。
A、有两个角相等的三角形是等腰三角形
B、等腰三角形一腰上的高与底边的夹角等于顶角的一半
C、等腰三角形两底角相等
D、有一个角的平分线平分对边的三角形一定是等腰直角三角形
04．已知△ABC三边长分别为2n+1，2n2+2n，2n2+2n+1，(n为正整数)，则△ABC为（ ）。
A、直角三角形 B、等腰三角形 C、锐角三角形 D、钝角三角形
05．某工厂计划用两个月把产量提高21％，如果每月比上月提高的百分数相同，求这个百分数。若设每月提高的百分数为x，原产量为a，可列方程为a(1+x)2=a(x+21％)，那么解此方程后依题意作答，正确的是（ ）。
A、这个百分数为2.1％或10％
B、x1=2.1，x2=0.1
C、x1= -2.1，x2=0.1 D、这个百分数为10％
06．如图，在△MBN中，BM=6，点A、C、D分别在MB、NB、MN上，四边形ABCD为平行四边形，且∠NDC=∠MDA，则□ABCD的周长是（ ）。
A、24 B、18 C、16 D、12
07．下列说法正确的是（ ）。
A、一颗质地均匀的骰子已连续抛掷了2000次，其中，掷出5点的次数最少，则第2001次一定能抛掷出5点
B、某种彩票中奖的概率是1％，因此买100张该种彩票一定会中奖
C、天气预报说明天下雨的概率是50％，那么明天有一半时间会下雨
D、抛掷一枚图钉，钉尖触地和钉尖朝上的概率不相等
08．函数y=kx+b(k≠0)与
(k≠0)在同一直角坐标系中的图象可能是（ ）。
 | |||
 | |||
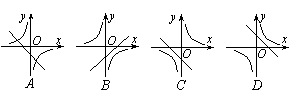二．填空题(本题共8小题，每小题3分，共24分)将每小题的正确结果直接填写在题中的横线上。
09．用配方法解一元二次方程x2+8x-9=0时，当配成完全平方后，原方程可变为 。
10．若边长为a的菱形有一个内角为60°，则它的面积为 。
11．如图，在△ABC中，AB=AC，BD、CE是△ABC的角平分线，请你至少写出除AB=AC以外的三组相等线段，它们是 。
12．跳水运动员在进行10m跳台跳水训练时，在正常情况下，运动员必须在距水面5m以前(含5m)完成规定的翻腾动作，并且调整好入水姿势，否则就容易出现失误。假设运动员起跳后的运动时间t(s)和运动员距离水面的高度h(m)满足关系式：h=10+2.5t-t2，那么运动员在保证不失误的情况下，完成动作时间的最大值是
。(结果可保留根号)
13．主视图和左视图都是矩形的物体是 形。
14．如图①，ABCD是一张正方形纸片，E、F分别为AB、CD的中点，沿过点D的折痕将A角翻折，使得点A落在EF上(如图②)，折痕交AE于点G，那么∠ADG等于 度。
15．已知反比例函数y=(2k-1)x
的图象有两点P(x1，y1)、Q(x2，y2)，且当x1＜x2＜0时，y1＞y2，则其函数的解析式为
。
16．不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同)，其中白球有3个，黄球1个，现从中任意摸出一个是白球的概率是
，那么袋中蓝球有
个。
三．解答题：(共72分)
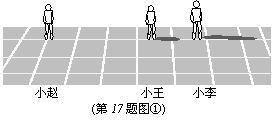
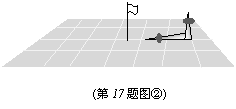
17．(本题满分7分)下列有两幅图，图①和图②。
(1)画图确定图①中路灯灯泡的位置，并画出此时小赵在路灯下的影子；
(2)画出图②中旗杆在阳光下的影子。
 | |||
 | |||
18．解下列方程 (每小题4分，共8分)
（1） 3(x-2)2 = 54 （2）2x2－4x-1=0
19．(本题满分8分)某建筑工地要靠一方院墙围建一个面积为130m2的矩形临时仓库，如图所示。已知可利用的院墙长16m，要求在与院墙平行的一边开一个宽为1m的门，现有的砖料按要求只能砌成32m长的围墙，求这个待建临时仓库的长和宽。
20．(本题满分8分)如图，小明站在残墙前，小亮在残墙后面活动，又不被小明看见。
(1)画出该实景图的俯视图；
(2)在俯视图中画出小亮的活动区域，对于小明而言，小亮的活动区域应称为小明的什么？
 |
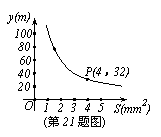21．(本题满分9分)你吃过拉面？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数，其图象如图所示。
(1)写出y与S的函数关系式；
(2)求当面条粗1.6mm2时，面条的总长度是多少米？
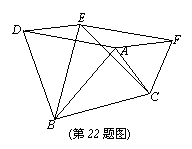
22．(本题满分10分)如图，以△ABC的三边为边，在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF，那么，四边形AFED是否为平行四边形？如果是，请证明之，如果不是，请说明理由。
 |
23．(本题满分10分)两人去某风景区游玩，每天某一时段开往该风景区有三辆汽车(票价相同)，但是他们两人不知道这些车的车况好坏，也不知道汽车开过来的顺序，两人采取了不同的乘车方案：甲无论如何总是上开来的第一辆车，而乙则是先观察后上车，当第一辆车开来时，他不上车，而是仔细观察车的舒适状况，如果第二辆车的舒适程度比第一辆好，他就上第二辆；如果第二辆车不比第一辆好，他就上第三辆车。若将这三辆车的舒适程度分为上、中、下三等，请你尝试解决如下问题：
(1)三辆车按出现的顺序共有哪几种不同的可能？(请一一列举出来)
(2)你认为甲、乙两人采用的乘车方案哪一人采用的方案使自己乘上等车的可能性大？为什么？
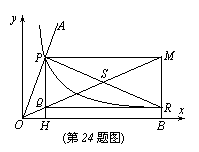
24．(本题满分12分)“三等分角”是数学史上一个著名的问题，但仅用尺规不可能三等分角，下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图)：将给定的锐角∠AOB置于平面直角坐标系中，边OB在x轴上，边OA与函数
(x＞0)的图象交于点P，以P点为圆心，2OP为半径作弧交图象于点R，分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连结OM，则∠MOB=∠AOB，要明白帕普斯的方法，请解决以下问题：
(1)设P(a，
)、R(b，
)，求直线OM对应的函数表达式(用含a、b的代数式表示)；
(2)分别过点P和R作y轴和x轴的平行线，两直线相交于点Q，请说明Q点在直线OM上，并证明：∠MOB=∠AOB；
(3)应用上述方法得到的结论，你认为如何三等分一个钝角？试用文字语言简要说明。
