九年级数学上册期末复习题
一．选择题（每小题3分。共24分）
1. 已知四边形
中，
，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（ ）
A．
B．
C．
D．
2. 在一个暗箱里放有a个除颜色外其它完全相同的球，这a个球中红球只有3个．每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在25%，那么可以推算出a大约是（ ）
A．12 B．9 C．4 D．3
3. 将如图所示的Rt△ABC绕直角边AC旋转一周，所得几何体的主视图是（ ）
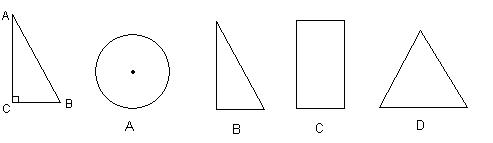
4. 如图，两个全等的长方形与
，旋转长方形
能和长方形重合，则可以作为旋转中心的点有（ ）
A．1个 B．2个 C．3个 D．无数个
5. 如图，在矩形ABCD中，AB＝3，BC＝4，点P在BC边上运
动，连结DP，过点A作AE⊥DP，垂足为E，设DP＝
，AE
＝
，则能反映与之间函数关系的大致图象是（ ）
6. 
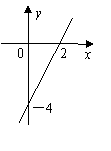小芳和爸爸正在散步，爸爸身高1.8m，他在地面上的影长为2.1m．若小芳比爸矮0.3m，则她的影长为（ ）．
A、1.3m B、1.65m C、1.75m D、1.8m
7. 已知一次函数
的图象如图所示，当
时，
的取值范围是（ ）
Ａ．
Ｂ、
Ｃ．
Ｄ．
8. 对于反比例函数
，下列说法不正确的是（ ）
A．点
在它的图象上 B．它的图象在第一、三象限
C．当
时，随的增大而增大 D．当
时，随的增大而减小
二．填空题（每小题3分。共24分）
9. 
若关于的一元二次方程
没有实数根，则
的取值范围是
．
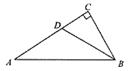
10.
如图，
中，∠C=90°，∠ABC=60°，BD平分∠ABC，
若AD=6，则CD= 。
11. 在“妙手推推推”的游戏中，主持人出示了一个9位数
| 2 | 5 | 8 | 3 | 9 | 6 | 4 | 1 | 7 |
让参加者猜商品价格。被猜的价格是一个4位数，也就是这 个9位中从左到右连在一起的某4个数字。如果参与者不知道商品的价格，从这些连在一起的所有4位数中，任意猜一个，他猜中该商品价格的概率 。
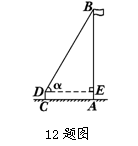
12．如图，小鸣将测倾器安放在与旗杆AB底部相距6m的C处，量出测倾器的
高度CD＝1m，测得旗杆顶端B的仰角
＝60°，则旗杆AB的高度为
（计算结果保留根号）
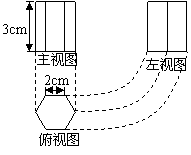
13．如图所示是某种型号的正六角螺母毛坯的三视图，则它的表面积为 
．
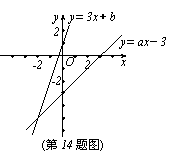
14．如图，已知函数y＝3x＋b和y＝ax－3的图象交于点P(－2，－5)，则根据图象可得不等式3x＋b＞ax－3的解集是_______________。
15．将正整数按如图所示的规律排列下去。若用有序实数对（
，
）表示第排，从左到右第个数，如（4，3）表示实数9，则（7，2）表示的实数是
。
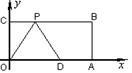16．已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（10，0）、C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为
。
三．解答题（本大题共9个小题，满分72分）.
17．计算（5分） 
；
18．先化简，再求值（7分）：
，其中
。
19．解方程（5分） 
．
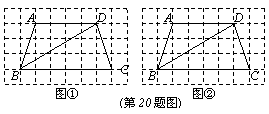
20. （8分）图①是等腰梯形ABCD，其中AD∥BC，AB＝DC．图②是与图①完全相同的图形．
（1）请你在图①、图②的梯形ABCD中各画一个与△ABD全等但位置不同的三角形，使三角形的各顶点在梯形的边(含顶点)上；
（2）选择（1）中所画的一个三角形说明它与△ABD全等的理由．
 |
21．（8）在一次数学活动中，黑板上画着如图所示的图形，活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式：
①
②
③
④
小明同学闭上眼睛从四张纸片中随机抽取一张，再从剩下的纸片中随机抽取另一张．请结合图形解答下列两个问题：
（1）当抽得①和②时，用①，②作为条件能判定
是等腰三角形吗？说说你的理由；
（2）请你用树状图或表格表示抽取两张纸片上的等式所有可能出现的结果（用序号表示），并求以已经抽取的两张纸片上的等式为条件，使不能构成等腰三角形的概率．
22． (8分)如图①，在等腰梯形ABCD中，AB∥CD，E、F是边AB上的两点，且AE＝BF，DE与CF相交于梯形ABCD内一点O．
(1)求证：OE＝OF；
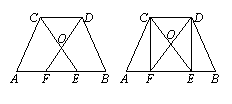(2)如图②，当EF＝CD时，请你连接DF、CE，判断四边形DCEF是什么样的四边形，并证明你的结论．
图1 图2
23、（9分）某县在实施“村村通”工程中，决定在A、B两村之间修筑一条公路，甲乙两个工程队分别从A，B两村同时相向开始修筑，施工期间，乙队因另有任务提前离开，余下的任务四甲队单独完成，直到道路修通，下图是甲乙两个工程队修道路的长度Y（米）与修筑时间x（天）之间的函数图象，请根据图象所提供的信息，求该的公路的总长度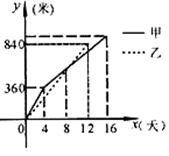
24．（ 10分）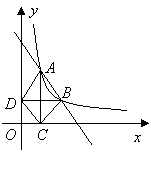
如图9，在直角坐标平面内，函数
（，是常数）的图象经过
，
，其中
．过点
作轴垂线，垂足为
，过点
作轴垂线，垂足为
，连结
，
，
．
（1）若
的面积为4，求点的坐标；
（2）求证：
；
（3）当时，求直线
的函数解析式．
25．（12分）已知
与
是反比例函数
图象上的两个点．
（1）求的值；
（2）若点
，则在反比例函数图象上是否存在点，使得以
四点为顶点的四边形为梯形？若存在，求出点的坐标；若不存在，请说明理由．
 |
参考 答案
一．选择题
1．D 2、A 3.D 4.A 5.C 6.C 7.C 8.C
二．填空题
9．K＜-1 10.3 11.
12.
6
+1 13.36+12
14.X＞-2 15. 23 16.(3,4) (2,4)(8,4)
三．解答题
17——20略 21、概率为
22、矩形 23、1800米
24、（1）点B（3，
） （3）①y=-2x+6
②y=-x+5
25(1).k=2 (2)(6,
)或（1，2）或（-2，-）