九年级数学上期期中试卷
全卷分A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟。
学生姓名 .班级 .学号 .得分:
A卷 (共 100分)
一、选择题(每小题3分,共24分)
1.下列是一元二次方程的是 ( )
| A. | B. |
| C. | D. |
2.下列四幅图形中,表示两颗小树在同一时刻阳光下的影子的图形可能是 ( )。

3.用配方法解方程![]() ,配方后的方程是 ( )
,配方后的方程是 ( )
| A. | B. |
| C. | D. |
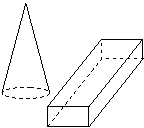
4.桌面上放着一个圆锥和一个长方体,其中俯视图应该是 ( )
|
|
|
(B) |
| (C) |
(D) |
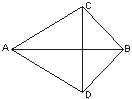 5 . 3. 如图,AC=AD,BC=BD.则 ( )
5 . 3. 如图,AC=AD,BC=BD.则 ( )
| A.CD垂直平分AB | B.AB垂直平分CD |
| C.CD平分∠ACB | D.以上结论都不正确 |
6. 如果两点P1(1,y1)和P2(2,y2)在反比例函数![]() 的图象上,那么y1与y2间的关系是 (
)
的图象上,那么y1与y2间的关系是 (
)
A.y2<y1<0 B.y1<y2<0 C.y2>y1>0 D.y1>y2>0
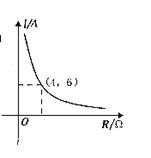
7.
|
成反比例,其函数图象如图所示,则电流![]() 与电阻R之间的函
与电阻R之间的函
数关系式为 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
8.对于中点四边形(顺次连接四边形各边中点的四边形),说法正确的个数是 ( )
①任何四边形的中点四边形是平行四边形.
②中点四边形的面积是原四边形面积的一半.
③矩形的中点四边形是矩形.
④等腰梯形的中点四边形是菱形.
| A. 1个 | B. 2个 | C. 3个 | D. 4个 |
二、填空题(每小题3分,共24分)
9.方程:![]() 的根是
.
的根是
.
10. 四边形ABCD中,对角线AC、BD交于点O, 若OA=OB=OC=OD,则这个四边形是
11. 等腰三角形的两边长为4和9,则这个等腰三角形的周长为 。
12、 已知2是关于![]() 的方程
的方程![]() 的一个解,则
的一个解,则![]() 的值是 .
的值是 .
 13. 若函数
13. 若函数![]() 的图象过点(3,-4),那么它一定还经过点 (-2, ).
的图象过点(3,-4),那么它一定还经过点 (-2, ).
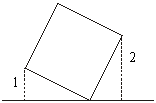
14. 一个正方形(如右图所示)摆放在
桌面上,则正方形的边长为 .
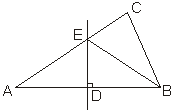 15.如右图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,则BC的长是 .
15.如右图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,则BC的长是 .
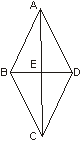 16.如右图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm,则对角线AC长为
,菱形ABCD的面积为
.
16.如右图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm,则对角线AC长为
,菱形ABCD的面积为
.
三、(每小题6分 共18分)
17.解答下列各题
(1)确定图中路灯灯泡的位置,并画出小赵在灯光下的影子;

(2)、解方程:![]()
(3)如果一元二次方程x2-6x-7=0的两个根是x1,x2,那么x1+x2=______________ , ![]() =_________.
计算
=_________.
计算![]() 的值。
的值。
四、(每小题8分,共16分)
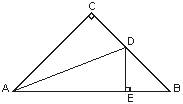 18. 如图,在Rt△ABC中,∠C=90o,AC=BC,AD平分∠CAB,DE⊥AB于E。若CD=4cm,求AC的长。
18. 如图,在Rt△ABC中,∠C=90o,AC=BC,AD平分∠CAB,DE⊥AB于E。若CD=4cm,求AC的长。
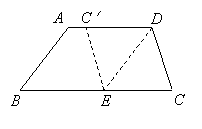 19. 如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
19. 如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
求证:四边形CDC′E是菱形.
五、(每小题9分,共18分)
20. “便民”水泥代销点销售某种水泥,每吨进价为250元.如果每吨销售价定为290元时,平均每天可售出16吨。现代销点采取降低促销的方式,若每吨售价每降低5元,则平均每天能多售出4吨.问:每吨水泥的实际售价定为多少元时,每天的销售利润平均可达720元 ?

| |
| |
(1) 求k的值;
(2) 求A、B两点的坐标;
(3) 求△AOB的面积;
 B卷(共50分)
B卷(共50分)
一、填空(每小题3分,共15分)
22.由几个相同的小正方体叠成一个几何体,它的三种视图如下所示,那么这个几何体是由 个小正方体组成。
 | |||||
 |  | ||||
(主视图) (俯视图) (左视图)
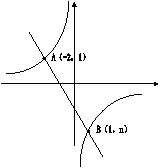
23. 如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于A、B两点,根据图像写出使一次函数的值大于反比例函数的值的
的图像相交于A、B两点,根据图像写出使一次函数的值大于反比例函数的值的![]() 的取值范围是
的取值范围是
24.若关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则
有实数根,则![]() 的取值范围是
.
的取值范围是
.
25.某药品原价每盒![]() 元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒
元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒![]() 元,则该药品平均每次降价的百分率是__ ____.
元,则该药品平均每次降价的百分率是__ ____.
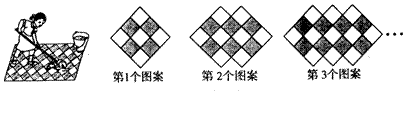 26.
如图,用灰白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖数为___________
26.
如图,用灰白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖数为___________

二、解答题(每小题7分,共14分)
27.(如右图所示)两个长宽分别为7cm、3cm的
矩形如图叠放在一起,则图中阴影部分的面积是多少?

28.如图,新星学校准备围成一个中间隔有一道篱笆的长方形花圃,现有长为24m的篱笆,一面靠墙(墙长为10 m).
设花圃宽AB为x(m),面积为S(m2).
(1)求S与x的函数关系式.
(2)如果要围成面积为45 m2的花圃,AB的长是多少?
三、(共10分)
29.如图,正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到正方形
后得到正方形![]() ,边
,边![]() 与
与![]() 交于点
交于点![]() . (1)以图中已标有字母的点为端点连结两条线段(正方形的对角线除外),要求所连结的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;
. (1)以图中已标有字母的点为端点连结两条线段(正方形的对角线除外),要求所连结的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;
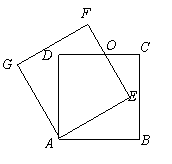 (2)若正方形的边长为
(2)若正方形的边长为![]() ,重叠部分(四边形
,重叠部分(四边形![]() )的面积为
)的面积为![]() ,求旋转的角度
,求旋转的角度![]() .
.
解:(1)我连结的两条相交且互相垂直的线段是______和______.
理由如下:
(2)
四、(共11分)30. 探索一个问题:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)
1).当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:设所求矩形的两边分别是![]() ,由题意得方程组:
,由题意得方程组:
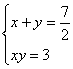 ,消去y化简得:
,消去y化简得:![]()
∵△=49-48>0 ∴![]() ∴满足要求的矩形B存在.
∴满足要求的矩形B存在.
2).如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
3).如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?
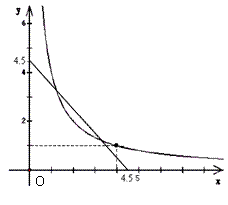 4).如图,在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象,其中x和y分别表示矩形B的两边长,请你结合刚才的研究,回答下列问题:
4).如图,在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象,其中x和y分别表示矩形B的两边长,请你结合刚才的研究,回答下列问题:
① 这个图象所研究的矩形A的两边长为___ __和__ ___;
② 满足条件的矩形B的两边长为___ __和___ __。
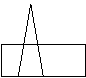
 (A)
(A)