九年级数学上学期试题

九年级数学上学期试题

（满分：150分　　　 考试时间：120分钟）

第一部分　　选择题（共36分）

题号 1 2 3 4 5 6 7 8 9 10 11 12 答案

一、选择题（下列各题只有一个答案是正确的.每小题3分,共36分）

1、下列根式与是同类二次根式的是　　　　　　　　　　　　　 

A、　　　B、　　 C、　　D、

2、两圆半径分别为4和6，圆心距为2，则两圆位置关系为

A、外离　　　　  B、相交　　　　  C、外切　　　　　 D、内切

3、对甲、乙两同学100米短跑进行5次测试，他们的成绩通过计算得；=，S²_甲=0.025,　 S²_乙=0.026下列说法正确的是　　　　　　  　　　　　　 

A.甲短跑成绩比乙好　　　 B.乙短跑成绩比甲好

C.甲比乙短跑成绩稳定　　D.乙比甲短跑成绩稳定

4、如图，抛物线的顶点坐标是P(1，3)，则函数y随自变量x的增大而减小的x的取值范围是

A．x>3　　　 B．x<3　　　 C．x>1　　　 D．x<1

5、式子有意义，则点P(a，b)在　　　　

A．第一象限　　 B．第二象限　　 C．第三象限　　 D．第四象限

6、二次函数的图象如何移动就得到的图象

A.向左移动1个单位，向上移动3个单位；

B.向右移动1个单位，向上移动3个单位

C.向左移动1个单位，向下移动3个单位；

D.向右移动1个单位，向下移动3个单位。

7、下列关于的一元二次方程的一个根是0，则

A、1　　　　B、　　　C、1或　　　D、0.5

8、一个直角三角形斜边长为，内切圆半径为，则这个三角形周长是

　A、　 B、　　C、　　 D、

9、校园内有一个半径为5米的圆形草坪，一部分学生为走“捷径”，在草坪内走出了一条小路，如图6所示. 通过计算可知，这些学生仅仅少走了（　 ）步，却踩坏了花草.（假设2步为1米，结果保留整数）

A. 1　　　　B. 2　　　　 C. 3　　　　 D. 4

10、如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是　

A、50　  B、62　　C、65　  D、68

11、已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=-1，P₁（x₁，y₁），P₂（x₂，y₂）是抛物线上的点，P₃（x₃，y₃）是直线l上的点，且-1＜x₁＜x₂，x₃＜-1，则y₁，y₂，y₃的大小关系为

A. y₁＜y₂＜y₃　B. y₃＜y₁＜y₂  C. y₃＜y₂＜y₁  D. y₂＜y₁＜y₃

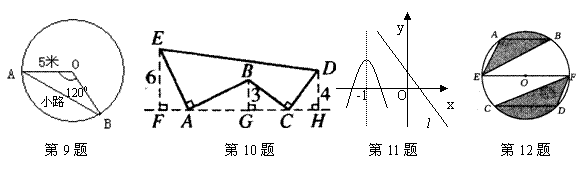12、如图，⊙O的直径EF为10cm，弦AB、CD分别为6cm、8cm，且AB∥EF∥CD．则图中阴影部分面积之和为
A、 　 B、 C、　D、

第二部分　　非选择题（共114分）

 二、填空题（每题3分,共24分）

13、在实数范围内定义一种运算“﹡”，其规则为a﹡b=a²-b²,根据这个规则，方程x﹡5=0的解为____________

14、当时，=　　　　　　 

15、数据70、71、72、73、69的标准差是_______________

16、抛物线y=(x-1)²-3的顶点坐标为　　　　　　　 

17、若梯形的中位线长为4，高为6，则此梯形的面积为　　　　　

18、读诗词“大江东去，浪淘尽，千古风流人物。而立之年，督东吴，早逝英年两位数，十位恰小个位三，个位平方与寿符。哪位学子算得快，多少年华属周瑜？”答：　　岁

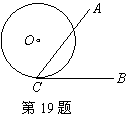
19、如图，∠ACB＝60º，半径为2的⊙O切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为　　

20、请看下列命题:

　①若分式的值为0,则x=0或1

　②两圆的半径R、r分别是方程x²-3x+2=0的两根，且圆心距d=3，则两圆外切

　③函数y=的图象既是轴对称图形又是中心对称图形.

④方程,有3个实数根.

其中，正确的命题有　　　　　　　　　　　　　　　　　　　　　 （填序号）

三、解答下列各题（21、22、23每题9分，共27分）

21. 解方程: 　

22. 先化简，再求值：，其中,　

 

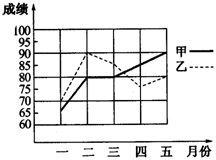
23. 为了从甲、乙两名学生中选拔一人参加全国数学竞赛，李老师每个月对他们的竞赛成绩进行一次测验，下图是两人赛前5次测验成绩的折线统计图．

①分别求出甲、乙两名学生5次测验成绩的平均数、极差及方差并且填在下表中；

②请你参谋一下，李老师应选派哪一名学生参加这次竞赛．请结合所学习的统计知识说明理由．　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　

解:(1) 填表如下:

	平均数	极差	方差
甲
乙
	平均数	极差	方差
甲
乙

	平均数	极差	方差
甲
乙

(2) 李老师应选派　　　　 参加这次竞赛．

理由：

四、(本题满分9分)

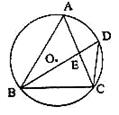
24．如图，已知ΔABC内接于⊙O，D是⊙O上一点，连结BD、CD，AC、BD交于点E．

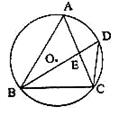（1）请找出图中的相似三角形，并加以证明；

（2）若∠D＝45°，BC＝4，求⊙O的面积．

五、(本题满分9分)

25．某水果批发商场经销一种高档水果 如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？

六、(本题满分10分)

26. NBA的一场篮球比赛中，一队员正在投篮，设篮球的运动的路线为抛物线（如图），其解析式为y=-x²+x+。

（1）这次投篮中球在空中飞行的水平距离是多少米时高度达到最大，最大高度是多少米？

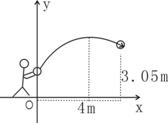（2）若投篮时出手地点与篮圈中心的水平距离为4米，篮圈距地面3．05米，问此球能否准确投中？（不考虑其它因素）

七、(本题满分10分)

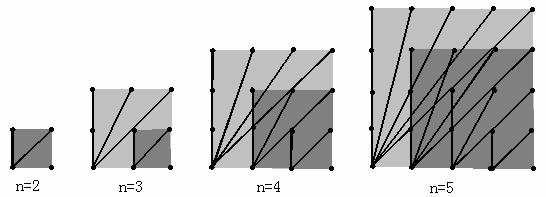27.探索n×n的正方形钉子板上(n是钉子板每边上的钉子数)，连接任意两个钉子所得到的不同长度值的线段种数：

当n=2时，钉子板上所连不同线段的长度值只有1与，所以不同长度值的线段只有2种，若用S表示不同长度值的线段种数，则S=2；

当n=3时，钉子板上所连不同线段的长度值只有1，，2，，2五种，比n=2时增加了3种，即S=2+3=5。

(1)　  观察图形，填写下表：

钉子数(n×n)	S值
2×2	2
3×3	2+3
4×4	2＋3＋(　　 )
5×5	(　　　　　　　　 )

(2)　  写出(n－1)×(n－1)和n×n的两个钉子板上，不同长度值的线段种数之间的关系；(用式子或语言表述均可)

八、(本题满分12分)

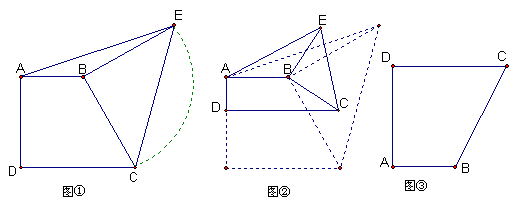
28. 在直角梯形ABCD中,AB⊥AD,CD⊥AD.将BC按逆时针方向绕B点旋转90°得到线段BE,并连接AE、CE(如图①)

（1）若AB=2cm,DC=3cm。求证：S_△ABE=1cm²

（2）图①中，将线段DC向上平行移动（其它条件保持不变），梯形ABCD和△ABE的形状就会变化，如图②所示，如果DC一直移动到AB的上方，得到如图③。请在下图的基础上将图③画完整。（不需要画出表示BC旋转方向的虚线）

(3)在图③中,若AB=a,CD=b(a<b)求S_△ABE

九、(本题满分13分) 

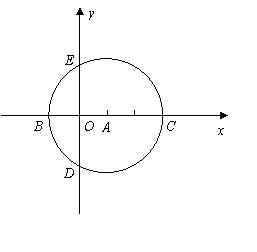
29. 如图，在直角坐标系中，以点A（，０）为圆心，以2为半径的圆与ｘ轴相交于点B，C，与ｙ轴相交于点D，E．

（1）若抛物线ｙ＝x²＋bx＋c经过C，D两点，求抛物线的解析式，并判断点B是否在该抛物线上．

（2）在（1）中的抛物线的对称轴上求一点P，使得△PBD的周长最小．

（3）设Q为（1）中的抛物线的对称轴上的一点，在抛物线上是否存在这样的点M，使得以B、C、Q、M是平行四边形．若存在，求出点M的坐标；若不存在，说明理由．