九年级数学月考测试卷（10月）
班级 姓名 学号
一．选择题（每题3分，共30分）
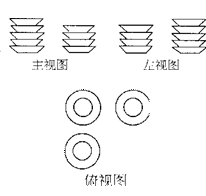
1．水杯的俯视图是（ ）
A B C D
2．如果
是一元二次方程，则（ ）
A． 
B．
C．
D．
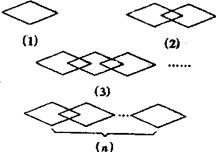
3．用配方法将二次三项式
变形，结果是 （ ）
(A) 
(B) 
(C) 
(D) 
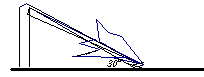
4．如图，一棵大树在一次强台风中于离地面5米处折断倒下，倒下部分与地面成30°夹角，这棵大树在折断前的高度为（ ）
A．10米 B．15米 C．25米 D．30米
5．已知等腰三角形的周长为40cm，以一腰为边作等边三角形，其周长为45cm，那么等腰三角形的底边长为（ ）
(A)5cm (B)10cm (C)15cm (D)20cm
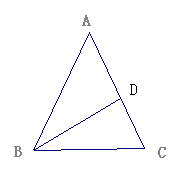
6.如图 ,加条件能满足AAS来判断⊿ACD≌⊿ABE的条件是（ ）
A．∠AEB = ∠ADC ∠C = ∠D B．∠AEB = ∠ADC CD = BE
C．AC = AB AD = AE D．AC = AB ∠C =∠B
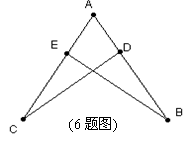
7．如图，在△ABC中，AB=AC，BD平分ABC交AC边于点D，∠DBC=35°，则∠A的度数为（ ）
A．35° B．40°
C．70° D．110°
 | |||
| |||
8．在同一时刻的阳光下，小刚的影子比小亮的影子长，那么在同一路灯下（ ）
(A)小刚的影子比小亮的影子长 (B)小刚的影子比小亮的影子短
(C)小刚的影子和小亮的影子一样长 (D)无法判断谁的影子长
9．商场在促销活动中，将标价为200元的商品，在打a折的基础上再打a折销售，现该商品的售价为128元，则a的值是（ ）
(A) 0.64
(B) 0.8
(C)8
(D) 6.4
10．如图，E、F、G、H分别是四边形ABCD四条边的中点，要使四边形EFGH为菱形，四边形ABCD应具备的条件是（ ）
A．
B．
C．
D．
二．填空题（每小题3分，共21分）
11.一张桌子上摆放着若干个形状和大小都相等的碟子，从三个方向上看，三种视图如上图所示，则这张桌子上最多有______个碟子.
12.某市教育经费从2003年的8千万元增加到2005年的9.68千万元，设这两年的教育经费平均增长率为x，则可列方程得__
13.找规律：如图，第（1）幅图中有一个菱形。第（2）幅图中有三个菱形，第（3）幅图中有5个菱形，则第（n）幅图中共有_______个菱形.
14．如果方程
的一个根是1，那么
的值是
，另一个根是 ；
15．在平行四边形ABCD中，对角线AC长为10
，∠CAB=30°，AB= 6，则平行四边形ABCD的面积为___________
；
16．在阳光明媚的星期天上午，小明和他父亲到沙滩上散步。小明发现他自己身高1.50m，在阳光下影长1.20m。其父亲身高1.70m，则此时其父亲的影长为___________m。
17．已知：如图，DC∥AB，且
,E为AB的中点，
观察图形，在不添加辅助线的情况下，请写出三个与△AED面积
相等的三角形：
______________________
三．解答题（69分）
19．解方程（每小题3分，共9分）
（1）x²+ 8x—9=0
（2）5x² =3x
（3）
20．已知，如图8，AB和DE是直立在地面上的两根立柱.AB=5m，某一时刻AB在阳光下的投影BC=3m.
（1）请你在图8中画出此时DE在阳光下的投影；（2分）
（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长.（4分）
 |
19．正方形网格中，小格的顶点叫做格点，以格点为顶点的正方形称为格点正方形，小华在图1的正方形网格中构造了一个以
为边的格点正方形，请你在图2和图3中分别构造以
和
为边的格点正方形．(6分)
22．（8分）某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出5件。若商场平均每天要盈利1600元，每件衬衫应降价多少元？
23．（6分）如图7，在 ABCD中，AM = AB, CN = CD。
求证：四边形AMCN是平行四边形.
24．海中有一个小岛A，该岛四周10海里内有暗礁。今有货轮由西向东航行，开始在A岛南偏西60°的B处，往东行驶20海里后到达该岛的南偏西30°的C处。之后，货轮继续向东航行。你认为货轮继续向东航行图中会有触礁的危险吗？请说明你的理由。（ 10分）
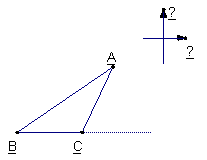
25．已知：如图，在⊿ABC中，AB＝AC，AD
BC，垂足为D，AN是△ABC外角
CAM的平分线，CEAN，垂足为E，连接DE交AC于F。（10分）
（1）求证：四边形ADCE为矩形；（4分）
（2）求证：DF∥AB，DF＝
AB；（4分）
（3）当⊿ABC满足什么条件时，四边形ADCE是一个正方形？简述你的理由。（3分）
 |
26．探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（完成下列空格）（14分）
（1）当已知矩形A的边长分别为6和1时，小明是这样研究的：设所求矩形的两边分别是
，由题意得方程组：
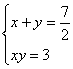，消去y化简得：
∵△＝49－48>0 ∴
∴满足要求的矩形B存在.
（2）如果已知矩形A的边长分别为2和1，请你仿照小明的方法研究是否存在满足要求的矩形B.
（3）如果矩形A的边长为m和n，请你研究满足什么条件时，矩形B存在？