九年级数数学质量检测卷
姓名 学号
一、选择题（本题共10小题，每小题4分，共40分）。
１、计算－１－２的值（）
Ａ、－１ Ｂ、－３ Ｃ、１ Ｄ、３
２、ｘ２－４=0的解是（）
Ａ、ｘ１=ｘ２=２ Ｂ、ｘ１=ｘ２=４ Ｃ、ｘ１=２，ｘ２=－２ Ｄ、ｘ１=４，ｘ２=４
３、
估计 ＋４的值是（）
Ａ、7和8之间 Ｂ、8和9之间 Ｃ、9和10之间 Ｄ、10和11之间
 |
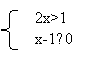４、不等式组 的解集是（）
Ａ、x>- 1/2 Ｂ、x<-1/2 Ｃ、x≤1 Ｄ、-1/2<x≤1
５、有一组数据如下：３，６，５，２，３，４，３，６，那么这组数据的中位数是（）
Ａ、3或4 Ｂ、4 Ｃ、3.5 Ｄ、3
６、已知三角形三个内角的度数之比是1：5：6，则其最大内角的度数是（）
Ａ、120° Ｂ、90° Ｃ、75° Ｄ、60°
７、抛物线的顶点坐标是（）
Ａ、（2，-11） Ｂ、（-2，7） Ｃ、（2，11） Ｄ、（2，-3）
８、已知关于x的一元二次方程x2－m=2x有两个不相等的实数根，则ｍ的取值范围是（）
Ａ、ｍ>-1 Ｂ、m<-2 Ｃ、m≥0 Ｄ、m<0
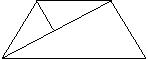
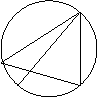
９、在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于Ｅ，ＡE=1，则梯形ABCD的高是（）
|
|
Ａ、1
Ｂ、
 |
|
|
|
１０、 将三粒均匀的分别标有1、2、3、4、5、6的正六面体骰子同时掷出，出现的数分别为a、b、c，则a、b、c正好是直角三角形三边长的概率是（）
 |  |  |  |
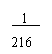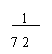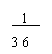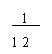Ａ、 Ｂ、 Ｃ、 Ｄ、
二、填空题（本题共6小题，每小题5分，共30分）
１１、 已知反比例函数图象经过（-1，2）点，则此反比例函数解析式是
１２、 因式分解：-2x3+4x2-2x=
１３、 ⊙O的弦长为8cm，弦心距为3cm，则⊙O的面积为 cm2
１４、 如图，△ABC是⊙O的内接三角形，AD是⊙O的直径，∠ABC=50o，∠ACD的度数是
１５、
|
|
已知x+y=9，且xy=12，
 |
| |||
|
|
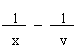１６、 已知点P（x，y）位于第二象限，并且y<x+4，x、y为整数，
请写出一个符合上述条件的点P的坐标
三、解答题（本题共8小题，共80分，务必写出解答过程。）
17、（本题８分）计算 －２-1 ＋︱
－２︱－３0
 |
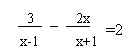18、（本题８分）解方程
19、（本题８分）用五点法画出函数的y=-x2+4x-3图象
|
|
|
|
|
|
20、（本题８分）已知矩形ABCD中，E是AD上一点，F是AB上一点，EF⊥EC，且EF=EC，DE=4cm，矩形ABCD的周长为32cm。求AE的长。
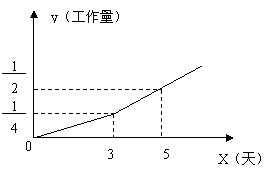
21、（本题10分）某家庭装修房屋，由甲、乙两个装修公司合作完成，先由甲装修公司单独装修三天，剩下工作由甲、乙两个装修公司合作完成，工程进度满足如图所示函数关系，该家庭共支付工资8000元。
（1） 完成此房屋装修共需要多少天？
（2） 若按完成工作量多少支付工资，甲装修公司应得多少元？
 |
22、（本题12分）一次足球训练中，一球员从球门正前方10m处将球射向球门，当球飞行的水平距离为6m时，球达到最高点，此时球离地面距离是3m。
（1） 以起脚点为原点，起脚点与球门地面中点所在直线为x轴，建立平面直角坐标系，请求出球运动抛物线的解析式。
（2） 已知球门高度为2.44m，问球能否射入球门？
23、（本题12分）学校准备组织290名学生进行野外考察活动，行李共100件，学校计划租用甲、乙两种型号汽车共8辆，经了解甲种汽车每辆最多能载40人和10件行李，乙种汽车每辆最多能载30人和20件行李。
（1） 设租用甲种汽车x辆，请你帮助学校设计所有可能的租车方案；
（2） 如果甲、乙两种汽车每辆的租车费分别为2000元，1800元，请你选择最省钱的一种租车方案。
 |
24、（本题14分）如图，对称轴为直线x= 的抛物线经过点A（6，0）和B（0，4）。
（1） 求抛物线解析式及顶点坐标；
（2）
设E（x，y）是抛物线上一个动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求 OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；
①当 OEAF的面积为24时，请判断
OEAF是否为菱形？
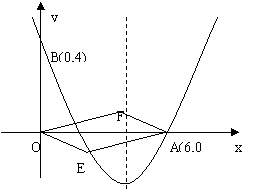
②是否存在点E，使 OEAF为正方形，若存在，求出E点坐标；若不存在，请说明理由。