 九年级数学第三次月考
九年级数学第三次月考
数 学 试 卷
| 题号 | 一 | 二 | 三 | 总分 | |||||||
| 1-10 | 11-16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | ||
| 得分 | |||||||||||
考生须知:
 1. 本卷共三大题,24小题. 全卷满分为150分,考试时间为120分钟.
1. 本卷共三大题,24小题. 全卷满分为150分,考试时间为120分钟.
2. 答题前,请用蓝、黑墨水的钢笔或圆珠笔将学校、姓名、学号
分别填在密封线内相应的位置上,不要遗漏.
3. 本卷不另设答题卡和答题卷,请在本卷相应的位置上直接答题.
答题必须用蓝、黑墨水的钢笔或圆珠笔(画图请用铅笔),答题
时允许使用计算器.
![]() 参考公式:二次函数
参考公式:二次函数![]() 图象的顶点坐标是
图象的顶点坐标是![]()
| 得分 | 评卷人 |
一.选择题(本题共10小题,每小题4分,共40分)请选出各
题中一个符合题意的正确选项填在相应的答案栏内,不选、
多选、错选均不给分.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
1. 若反比例函数![]() 的图象经过点(2,-3),则图象必经过另一点
的图象经过点(2,-3),则图象必经过另一点
A.(2,3) B.(-2,3) C.(3,2) D.(-2,-3)
2. 已知圆锥的底面半径为3,母线长为5,则圆锥的侧面积是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 将抛物线![]() 先向左平移1个单位,再向上平移1上个单位,得到的抛物线为
先向左平移1个单位,再向上平移1上个单位,得到的抛物线为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 已知![]() ,则
,则![]() 的值是
的值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
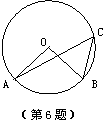 5.
如图,A、B、C三点在⊙O上,且∠AOB=80°,则∠C=
5.
如图,A、B、C三点在⊙O上,且∠AOB=80°,则∠C=
A.100° B.80° C.50° D.40°
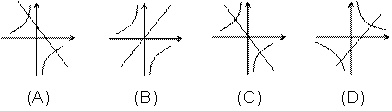
6. 在同一坐标系中函数![]() 和
和![]() 的大致图象是
的大致图象是
7. 对于下列命题中,正确的是
A.所有的直角三角形都相似 B.所有的等边三角形都相似
C.所有的等腰三角形都相似 D.所有的矩形都相似
8. 如果![]() 是锐角,且cos
是锐角,且cos![]() =
=![]() ,那么sin
,那么sin![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
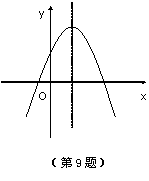
9. 已知二次函数![]() 的图象如图所示,则一次函数
的图象如图所示,则一次函数![]() 的图象不经过
的图象不经过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.探索以下规律,如图:
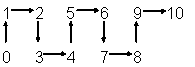 |
…,根据以上规律,从2006到2008的箭头方向正确的是
A. B. C. D.
| 得分 | 评卷人 |
二.填空题(本题共6小题,每小题5分,共30分)
11.在Rt△ABC中,已知∠C=900,AC=3,AB=5,则cosA= .
12.已知半径为6cm的圆中,600的圆心角所对的弧长为 cm.
13.请写出一个顶点在x轴上,且开口方向向下的二次函数: .
 14.已知△ABC∽△A1B1C1,且它们的相似比为
14.已知△ABC∽△A1B1C1,且它们的相似比为![]() . 如果△ABC的周长
. 如果△ABC的周长
为20cm,那么△A1B1C1的周长为 cm.
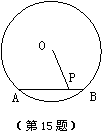
15.如图,已知⊙O的直径为10,弦AB=6,点P是弦AB上的一个动
点,那么OP的取值范围应该是 .
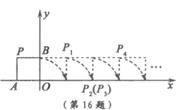 16.如图,将边长为1的正方形OAPB沿x轴正方向连续翻转
16.如图,将边长为1的正方形OAPB沿x轴正方向连续翻转
2007次,点P依次落在点P1,P2,P3,P4,…,P2007的位
置,则P2007的横坐标x2007=__________.
三.解答题(本题共8小题,共80分. 请务必写出解答过程)
| 得分 | 评卷人 |
17.(本题8分)计算: ![]() .
.
| 得分 | 评卷人 |

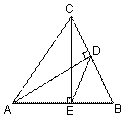 18.(本题8分)如图,在△ABC中,AD、CE是两条高,连结DE,如果
18.(本题8分)如图,在△ABC中,AD、CE是两条高,连结DE,如果
BE=2,EA=3,CE=4,在不添加任何辅助线和字母的条件下,请写出
三个正确结论(要求:分别为边的关系,角的关系,三角形相似的
关系),并对其中三角形相似的结论给予证明.
| 得分 | 评卷人 |
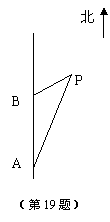 19.(本题8分)如图,一渔船正以每小时30海里的速度由南向北航行,在A处看见小岛P在船的北偏东30°方向上.2小时后,渔船行至B处,此时看见小岛P在船的北偏东75°方向上.求此时渔船距小岛P的距离BP.
19.(本题8分)如图,一渔船正以每小时30海里的速度由南向北航行,在A处看见小岛P在船的北偏东30°方向上.2小时后,渔船行至B处,此时看见小岛P在船的北偏东75°方向上.求此时渔船距小岛P的距离BP.
| 得分 | 评卷人 |
 20.(本题8分)现有9个相同的小正三角形拼成的大正三角形,将其部分
20.(本题8分)现有9个相同的小正三角形拼成的大正三角形,将其部分
涂黑.如图(1),(2)所示.
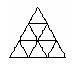
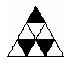

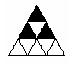
图(1) 图(2) 图(3) 图(4)
观察图(1),图(2)中涂黑部分构成的图案.它们具有如下特征:①都是轴对称图形②涂黑部分都是三个小正三角形.
请在图(3),图(4)内分别设计一个新图案,使图案具有上述两个特征.
| 得分 | 评卷人 |
21. (本题10分)
| |
AB=5,BC=3.
(1)求sin∠BAC的值;
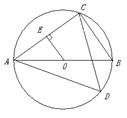
| |
(3)求tan∠ADC的值(结果保留根号).
| 得分 | 评卷人 |
22.(本题12分)某年级组织学生参加夏令营活动,本次夏令营分为甲、
乙、丙三组进行活动. 下面两幅统计图反映了学生报名参加夏令营
的情况,请你根据图中的信息回答下列问题:
报名人数分布直方图 报名人数扇形分布图
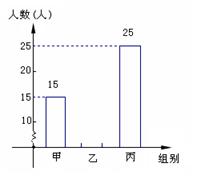
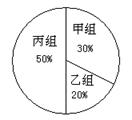
(1)该年级报名参加丙组的人数为 ;
(2)该年级报名参加本次活动的总人数 ,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,应从甲组抽调多少名学生到丙组?
| 得分 | 评卷人 |
23.(本题12分)初三(1)班数学兴趣小组在社会实践活动中,进
行了如下的课题研究:用一定长度的铝合金材料,将它设计成
外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验:
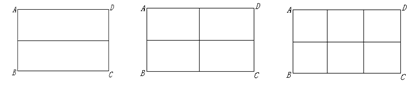
图案(1) 图案(2) 图案(3)
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,长方形框架ABCD的面积是 m2;
(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为![]() m,长方形框架ABCD的面积为S= (用含
m,长方形框架ABCD的面积为S= (用含![]() 的代数式表示);当AB= m时,框架ABCD的面积S最大;在图案(3)中,如果铝合金材料总长度为
的代数式表示);当AB= m时,框架ABCD的面积S最大;在图案(3)中,如果铝合金材料总长度为![]() m, 设AB为
m, 设AB为![]() m,当AB= m时, 长方形框架ABCD的面积S最大.
m,当AB= m时, 长方形框架ABCD的面积S最大.
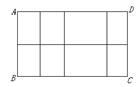 (3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存
(3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存
在着一定的规律. …
探索:
如图案(4), 如果铝合金材料总长度为![]() m,共有n条竖档时,
m,共有n条竖档时,
那么当竖档AB多少时,长方形框架ABCD的面积最大. 图案(4)
| 得分 | 评卷人 |
 24.(本题14分)如图,平面直角坐标系中,直线AB与
24.(本题14分)如图,平面直角坐标系中,直线AB与![]() 轴,
轴,![]() 轴分别
轴分别
交于A(3,0),B(0,![]() )两点,点C为线段AB上的一动点,过点
)两点,点C为线段AB上的一动点,过点
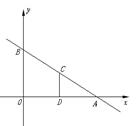 C作CD⊥
C作CD⊥![]() 轴于点D.
轴于点D.
(1)求直线AB的解析式;
(2)若S梯形OBCD=![]() ,求点C的坐标;
,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的三
角形与△OBA相似.若存在,请求出所有符合条件的点P的
坐标;若不存在,请说明理由.