二次函数综合测试卷
一、填空：(每空3分，共24分)
1．二次函数的图象经过三个定点（2，0），（3，0），（0，-1），则它的解析式为________，该图象的顶点坐标为__________．
2．抛物线y=x2-4x+11的对称轴是直线________，顶点坐标为________．
3．如果抛物线y=-
x2+（m+2）x+
m的对称轴为直线x=
，则m的值为_________．
4．将抛物线y＝x2向左平移4个单位后，再向下平移2个单位，则此时抛物线的解析式是 ．
5．如图，一小孩将一只皮球从A处抛出去，它所经过的路线是某个二次函数图象的一部分，如果他的出手处A距地面的距离OA为1 m，球路的最高点B(8，9)，则这个二次函数的表达式为______.
6．开口向下的抛物线y=a（x+1）（x-4）与x轴交于A、B两点，与y轴交于点C．若∠ACB=90°，则a的值为________．
y
B
A
x
O
5图
二、选择题：(7～12单选，每题3分，13～15为多选，每题4分，共30分)
7．在同一直角坐标系内，函数y=ax2+bx与y=
（b≠0）的图象大致为（ ）
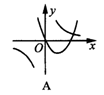
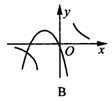
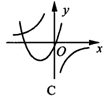
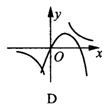
8．给出下列四个函数：y=-2x，y=2x-1，y=
（x>0），y=-x2+3（x>0），其中y随x的增大而减小的函数有（ ）
A．3个 B．2个 C．1个 D．0个
9．若二次函数y=x2－2x+c图象的顶点在x轴上，则c等于（ ）
A.－1 B.1
C.
D.2
10、把二次函数
的图象向左平移2个单位，再向上平移1个单位，所得到的图象对应的二次函数关系式是（ ）
（A）
; （B）
;
（C）
（D）
11、.已知二次函数y=x2+(2k+1)x+k2－1的最小值是0，则k的值是（ ）
A.
B.－
C.
D.－
12从一张矩形纸片ABCD的较短边AD上找一点E，过这点剪下两个半圆，它们的直径分别是AE、DE，要使剪下的两个半圆的面积和最小，点E应选在（ ）
A．边AD的中点外 B．边AD的
处 C．边AD的
处 D．边AD的
处
13、关于二次函数y=ax2+bx+c的图象有下列命题，其中是假命题的是（ ）
A、c=0时，函数的图象经过原点 B、b=0时，函数的图象关于y轴对称
C、数的图象最高点的纵坐标是
D、c>0且函数的图象开口向下时，方程ax2+bx+c=0必有两个不相等的实根
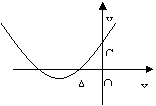14、y=ax2+bx+c的图象如图，OA=OC，则（ ）
（A） ac+1=b; B、a＞0,bc＞0
C、
＞0 D、a+b+c＜0
15、如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3,那么c的值等于（ ）
A、8 B、14、C、15、D、16
三、解答题：(66分)
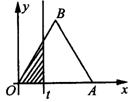
16、(6分)如图，△OAB是边长为2的等边三角形，直线x=t截这个三角形所得位于直线左方的图形面积为y．
（1）写出以自变量为t的函数y的解析式；（2）画出（1）中函数y的图象．
y
17、(8分)抛物线Y= -X
+ ( m 一 l ）与Y轴交于（ 0 , 3 ）点．
( 1 ）求出 m 的值并画出这条抛物线；
( 2 ）求它与 x 轴的交点和抛物线顶点的坐标 x
( 3 ) x 取什么值时，抛物线在X轴上方？
O
( 4 )X取什么值时，Y的值随 x 值的增大而减小？
18、(9分)已知一次函数y=ax+b的图象上有两点A、B，它们的横坐标分别是3，－1，若二次函数y=
x2的图象经过A、B两点.
(1)请求出一次函数的表达式;
(2)设二次函数的顶点为C，求△ABC的面积.
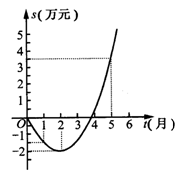
19．(9分)A公司推出一种高效环保洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数图象刻画了该公司年初以来累积利润S（万元）与销售时间t（月）之间的关系（即前t个月的利润总和S与t之间的关系）．
（1）由已知图象上的三点坐标，求累积利润S（万元）与时间t（月）之间的函数关系式；
（2）求截止到几月末公司累积利润可达到30万元；
（3）求第8个月公司所获利润多少万元？
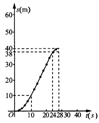
20、（9分)某商场试销一种成本为60元/件的T恤，规定试销期间单价不低于成本单价，又获利不得高于40%，经试销发现，销售量y（件）与销售单价x（元/件）符合一次函数y=kx+b，且x=70时，y=50；x=80时，y=40．
（1）求一次函数y=kx+b的表达式；
（2）若该商场获得利润为w元，试写出利润w与销售单价x之间的关系式；销售单价定为多少时，商场可获得最大利润，最大利润是多少？
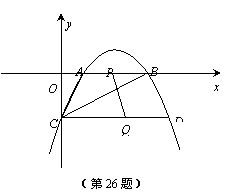
21、(11分)抛物线y＝－
x2＋
x－2与x轴相交于点A、B，与y轴相交于点C．
（1）求证：△AOC∽△COB；
（2）过点C作CD∥x轴交抛物线于点D．若点P在线段AB上以每秒1个单位的速度由A向B运动，同时点Q在线段CD上也以每秒1个单位的速度由D向C运动，则经过几秒后，PQ＝AC．
 |
22、(14分)如图抛物线y＝
，x轴于A、B两点，交y轴于点c，顶点为D。
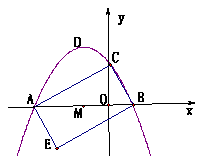1）求A、B、C的坐标。
2）把△ABC绕AB的中点M旋转180°，得到四边形AEBC：
①求E点坐标。
②试判断四边形AEBC的形状，并说明理由。
3）试探索：在直线BC上是否存在一点P，使得△PAD的
周长最小，若存在，请求出P点的坐标；若不存在，请说明
理由？