二次函数综合题集2
1、已知抛物线
经过A（-1，0）点 切经过直线
与坐标轴的两个交点B，C。
（1） 求抛物线的解析式；
（2） 求抛物线的顶点坐标；
（3） 若点M在第四象限内的抛物线上，且OM⊥BC，垂足为D，求点M的坐标.
2、已知开口向下的抛物线, 与x轴交于A(
,0),B(
,0)( ﹤)两点,与y轴交于C(0,5)点,若a+b+c=0且S△ABC=15, 求抛物线的解析式.
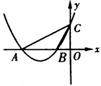3、 如图所示，已知抛物
与x轴负半轴交于A、B两点，与y轴交于点C，且
，求抛物线的解析式和它的顶点坐标.
4、已知直线y＝－2x＋b(b≠0)与x轴交于点A，与y轴交于点B；一抛物线的解析式为y＝x2－(b＋10)x＋c.
⑴若该抛物线过点B，且它的顶点P在直线y＝－2x＋b上，试确定这条抛物线的解析式；
⑵过点B作直线BC⊥AB交x轴于点C，若抛物线的对称轴恰好过C点，试确定直线y＝－2x＋b的解析式.
5、已知抛物线y=(1-m)x2+4x-3开口向下，与x轴交于A(x1,0)和B(x2,0)两点，其中xl<x2．
(1)求m的取值范围；
(2)若x12+ x22=10，求抛物线的解析式，并在给出的直角坐标系中画出这条抛物线；
6、如图，等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A( 0,6 )，D ( 4，6)，且AB=2
（1）求点B的坐标；（2）求经过A、B、D三点的抛物线的解析式；
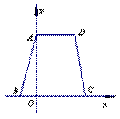（3）在（2）中所求的抛物线上是否存在一点P，使得S△PBD=S梯形ABCD。若存在，请求出该点坐标，若不存在，请说明理由.
7、数学活动小组接受学校的一项任务：在紧靠围墙的空地上，利用围墙及一段长为6０米的木栅栏围成一块生物园地，请设计一个方案使生物园的面积可能大。
(1)活动小组提交如图的方案。设靠墙的一边长为 x 米，则不靠墙的一边长为(60－2x)米，面积y= (60－2x) x米2．当x=15时，y最大值 =450米2。
(2)机灵的小明想：如果改变生物园的形状，围成的面积会更大吗？请你帮小明设计两个方案，要求画出图形，算出面积大小；并找出面积最大的方案．
8、已知二次函数
的图象经过点A(-3,6)，并与
轴交于B、C两点（点B在C的左边），P为它的顶点.
（1）试确定
的值；
（2）设点D为线段OC上的一点，且满足
，求直线AD的解析式；
（3）在
轴的正半轴上是否存在点M，使
为等腰三角形，若存在，求出所有满足条件的点M的坐标，若不存在，请说明理由.
9、已知：以直线
为对称轴的抛物线与轴交于
、
两点（点在点的左边），且经过点
和
. 点
在抛物线的顶点
的右侧的半支上（包括顶点），在轴上有一点
使
是等腰三角形，
.
（1）若
是直角，求点
的坐标；
（2）当点移动时，过点作轴的垂线，交直线
于点
，设
的面积为
，求关于的函数解析式和自变量的取值范围，并画出它的图象.
10、（2007四川成都）在平面直角坐标系
中，已知二次函数
的图象与轴交于
两点（点在点的左边），与轴交于点，其顶点的横坐标为1，且过点
和
．
（1）求此二次函数的表达式；
（2）若直线
与线段
交于点
（不与点
重合），则是否存在这样的直线
，使得以
为顶点的三角形与
相似？若存在，求出该直线的函数表达式及点的坐标；若不存在，请说明理由；
（3）若点是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角
与
的大小（不必证明），并写出此时点的横坐标
的取值范围．
．
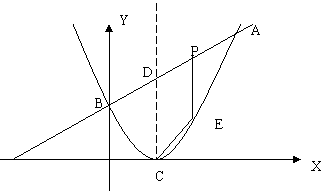
11、如图，已知二次函数图象顶点为C（1，0），直线
与该二次函数交于A，B两点，其中A点（3，4），B点在y轴上，（1）求m值及这个二次函数关系式；（2）P为线段AB上一动点（P不与A，B重合），过P做x轴垂线与二次函数交于点E，设线段PE长为h，点P横坐标为x，求h与x之间的函数关系式，并写出自变量x取值范围；（3）D为AB线段与二次函数对称轴的的交点，在AB上是否存在一点P，使四边形DCEP为平行四边形？若存在，请求出P点坐标；若不存在，请说明理由。
 |
12、已知：抛物线
顶点在直线
上，且仅当0﹤x﹤4时,y﹤0，设点A是抛物线与x轴的一个交点，点A在y轴的右侧，P为抛物线上的一个动点，
（1）求这个抛物线的解析式；（2）当△POA面积为5时，求点P坐标。（3）当cos∠OPA=
时，⊙M经过点O，A，P，求过A点且与⊙M相切的直线解析式
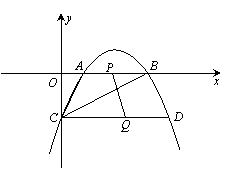
13、在平面直角坐标系xoy中，抛物线
经过P（
，5），A（0，2）两点。（1）求次抛物线解析式；（2）设抛物线顶点为B，将直线AB沿y轴向下平移两个单位的直线L，直线L与抛物线的对称轴交于C点，求直线的解析式；（3）在（2）的条件下，求到直线OB，OC，BC距离相等的点的坐标。
14．如图，抛物线y＝－
x2＋
x－2与x轴相交于点A、B，与y轴相交于点C．
（1）求证：△AOC∽△COB；
（2）过点C作CD∥x轴交抛物线于点D．若点P在线段AB上以每秒1个单位的速度由A向B运动，同时点Q在线段CD上也以每秒1个单位的速度由D向C运动，则经过几秒后，PQ＝AC．
 |
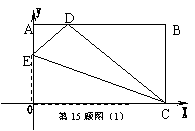
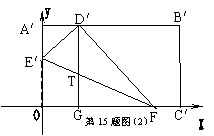
15.将一矩形纸片OABC放在直角坐标系中，O为原点，C在轴上，OA=6，OC=10.
⑴如图⑴，在OA上取一点E，将△EOC沿EC折叠，使O点落在AB边上的D点，求E点的坐标；
⑵如图⑵，在OA、OC边上选取适当的点E′、F，将△E′OF沿E′F折叠，使O点落在AB边上的D′点，过D′作D′G∥A′O交E′F于T点，交OC′于G点，求证：TG=A′E′
⑶在⑵的条件下，设T（，）①探求：与之间的函数关系式.②指出变量的取值范围.
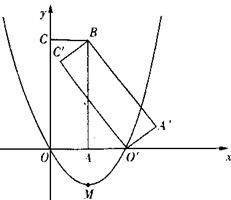
16、（2007四川眉山）如图，矩形A’BC’O’是矩形OABC(边OA在x轴正半轴上，边OC在y轴正半轴上)绕B点逆时针旋转得到的．O’点在x轴的正半轴上，B点的坐标为(1，3)．
(1)如果二次函数y＝ax2＋bx＋c(a≠0)的图象经过O、O’两点且图象顶点M的纵坐标为
—1．求这个二次函数的解析式；
(2)在(1)中求出的二次函数图象对称轴的右支上是否存在点P，使得ΔPOM为直角三角形?若存在，请求出P点的坐标和ΔPOM的面积；若不存在，请说明理由；
(3)求边C’O’所在直线的解析式．
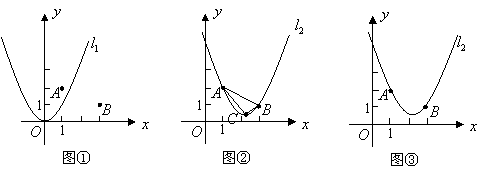
17、（2007山东威海）如图①，在平面直角坐标系中，点的坐标为
，点的坐标为
，二次函数
的图象记为抛物线
．
（1）平移抛物线，使平移后的抛物线过点，但不过点，写出平移后的一个抛物线的函数表达式：
（任写一个即可）．
（2）平移抛物线，使平移后的抛物线过两点，记为抛物线
，如图②，求抛物线的函数表达式．
（3）设抛物线的顶点为，
为轴上一点．若
，求点的坐标．
（4）请在图③上用尺规作图的方式探究抛物线上是否存在点，使
为等腰三角形．若存在，请判断点共有几个可能的位置（保留作图痕迹）；若不存在，请说明师．
 |