§3.3反比例函数
复习目标
1. 反比例函数：若两个变量x、y间的关系式可以表示成
(k ≠0）的形式，则称y是x的反比例函数。
2．反比例函数的图象及性质：
| 表达式 | y=(k≠0) | |
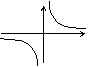
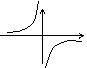
| 图 象 | k>0 | k<0 |
|
|
| |
| 性 质 | 1．图象在第一、三象限； 2．每个象限内，函数y的值随x的增大而减小． | 1．图象在第二、四象限； 2．在每个象限内，函数y值随x的增大而增大． |
典例精析
【例1】（2006黄冈）反比例函数
，当x＞0时，y随x的增大而增大，则m的值时（ ）
A、±1 B、小于
的实数 C、－1 D、1
【分析】本题考察反比例函数的定义及有关性质。反比例函数不仅有形式：(k ≠0），也可以改写成：
(k ≠0）。 又因为当x＞0时，y随x的增大而增大，所以k<0。
【解答】由题意可得：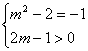
，解得
.因此选D。
【例2】(1)已知y与(2x+1)成反比例，且当x=1时，y=2，那么当x=0时，y=__________。
(2) 如果反比例函数
的图象经过点(―3，1)，那么k=______。
(3)若点(3，4)是反比例函数
图象上一点，则此函数图象必经过点( )。
A．(2，6) B。(2，―6) C。(4，―3) D。(3，―4)
【分析】以上几题考查了反比例函数的定义和利用待定系数法求反比例函数的解析式。
【解答】(1)依题意设y=
，∴当x=1时，y=
=2。
∴k=6， 
，故当x=0时，
。
(2)依题意得：当x=―3时，
=1。 ∴k=―3。
(3)由题意得：当x=3时，
。
∴
，y=
。 故选A。
注意：第(3)题要注意把m2+2m―1看作一个整体，体现了整体代入的思想。
【例3】(1)反比例函数y=
(k≠0)的图象的两个分支分别位于 ( )
A：第一、二象限 B：第一、三象限 C：第二、四象限 D：第一、四象限
(2) 设有反比例函数y=
。 (x1，y1)、(x2，y2)为其图象上两点，当x1＜0＜x2时，有y1>y2 ，则k的取值范围是______。
(3)当k＜0时，反比例函数y＝
和一次函数y＝kx＋2的图象在致是图中的( )。
【分析】以上几题考查了反比例函数的图象及其性质。
【解答】(1)∵k≠0， ∴k2>0，双曲线分布在一、三象限。选B。
(2)∵x1＜0＜x2时，有y1>y2∴画草图可知双曲线的图象分布在二、四象限，k+1<0。故填k<―1。
(3)∵k＜0， ∴反比例函数的图象落在二、四象限，一次函数 y随x的增大而减少。又y＝kx＋2的图象经过点(0，2)，故选B。
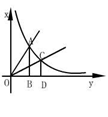
【例4】如图，正比例函数y=x及y=mx的图象与反 比例函数y＝
的图象分别交于第一象限内的A、C两点，过A、C分别向x轴作垂线，垂足分别为B、D。若直角三角形AOB与直角三角形COD的面积分别为S1、S2，则S1与S2的关系为( )。
A．S1>S2 B。S1=S2 C。S1<S2 D。与m、k的值有关
【分析】此题考查了反比例函数同一次函数、几何中的面积等知识相结合的综合问题。
【解答】设A、B的坐标为A(x1，y1)、B(x2，y2)。
则y1＝
，y2＝
。即x1·y1 =k，x2·y2=k
∵OB=
，AB=
，OD=
，CD=
。
∴S1=
， S2=
。故选B。
由此我们可以得出：过反比例函数y＝的图象图象上任一点，向x轴作垂线，这一点与垂足、原点所得到的直角三角形，其面积为
；若再向y轴作垂线，此时围成的矩形面积为
。
【例5】（2005江苏南京）一定质量的氧气，它的密度ρ（千克/米3）是它的体积V（立方米）的反比例函数，当V＝10立方米时，ρ＝1.43千克/米3
（1）求ρ与V的函数关系式。
（2）求当V＝2立方米时氧气的密度ρ。
【分析】本题与自然科学的相关知识联系在一起，属于一道学科综合题。题目本身其实比较简单，还是用待定系数法求反比例函数的解析式。
【解答】解：（1）设
，由题意可得：
所以
（2）当V＝2立方米时氧气的密度
千克/米3
课内巩固
1．（2005甘肃）下列各点在双曲线
上的是（ ）。
A．（1，2） B．（2，2） C．（4，2） D．（0，2）
2．（2005辽宁）反比例函数的图像经过点P（－4，3），则k的值等于（ ）。
A．12 B． 
C．
D．－12
3．（2005浙江）电压一定时，电流I与电阻R的函数图像大致是（ ）。
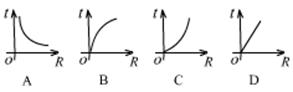
4．（2006遂宁）已知函数
(x>0),那么（ ）
A、函数图象在一象限内,且y 随x的增大而增大
B、函数图象在一象限内,且y 随x的增大而减小
C、函数图象在二象限内,且y 随x的增大而增大
D、函数图象在二象限内,且y 随x的增大而减小
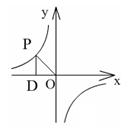
5．（2005江西）如图，点P是反比例函数
上一点，PD⊥x与点D，则△POD的面积是________。
6．（2005青海）近视眼睛的度数y（度）与镜片焦距x（米）成反比例，已知400度近视镜片的焦距为0.25米，则眼镜度数y与镜片焦距x之间的函数关系式为________。
7．若一次函数y＝x＋b与反比例函数的图像在第二象限内有两个交点，则k__0，b___0。（用 “＞”“＜”“＝”填空）。
8．在压力不变的情况下，某物体承受的压强p（Pa）是它的受力面积S（m2）的反比例函数，其图象如图所示．
(1) 求p与S之间的函数关系式；
(2) 求当S＝0.5 m2时物体承受的压强p．
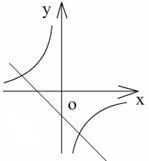9．（2005呼和浩特）如图，一次函数y＝kx＋b的图像与反比例函数
的图像交于A（－2，1），B（1，n）两点。
（1）求反比例函数和一次函数的表达式。
（2）根据图像写出使一次函数的值大于反比例函数的值时的x的取值范围。
课外拓展
A组
1.（2006诸暨）函数y=自变量x的取值范围是 （ ）
A．x＞0 B．x＜0 C．x=0 D．x≠0
2．（2006舟山）已知反比例函数的图象经过点（-2，1），则反比例函数的表达式为（ ）
A．y=-
B．y=
C．y=-
D．y=
3．（2006浙江）如果两点P1(1，y1)和P2(2，y2)在反比例函数
的图象上，那么（ ）
A．y2＜y1＜0 B．y1＜y2＜0 C．y2＞y1＞0 D．y1＞y2＞0
4．（2005江苏省宿迁）若直线
与双曲线的图象的一个交点坐标为（2，4）．则它们的另一个交点坐标是（ ）A
A．（－2，－4） B．（－2，4） C．（－4，－2） D．（2，－4）
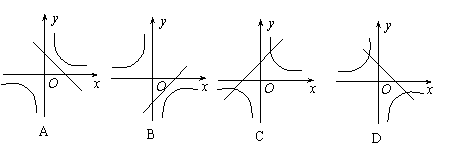5．（2005河北）在同一直角坐标系中，函数y=kx-k与
(k≠0)的图象大致是（ ）
6．（2006河北）某闭合电路中，电源的电压为定值，电流I（A）与电
阻R（Ω）成反比例．如图表示的是该电路中电流I与电阻R之间
关系的图象，则用电阻R表示电流I的函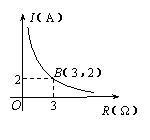
数解析式为 ．
7．己知反比例函数
(x >0)，y随x 的增大而增大，则m的
取值范围是 ．
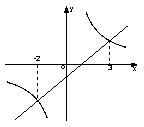
8．（2006旅顺）如图是一次函数y1=kx+b和反比例函数y2=
的图象，
观察图象写出y1＞y2时，
的取值范围 ．
9．（2006北京）在平面直角坐标系xOy中，直线y=－x绕点O顺时针
旋转90°得到直线l，直线l与反比例函数的图象的一个交点为
A(a，3)，试确定反比例函数的解析式。
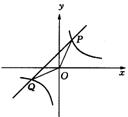10．如图，已知反比例函数
的图象与一次函数y＝kx＋4的图象相交于P、Q两点，并且P点的纵坐标是6．
（1）求这个一次函数的解析式；
（2）求△POQ的面积．
B组
11．给出下列函数：(1)y=2x; (2)y=-2x+1; (3)y=
(x>0) (4)y=x2(x<-1)
其中，y随x的增大而减小的函数是（ ）
A、（1）、（2）. B、（1）、（3）.
C、(2)、(4). D 、（2）、（3）、（4）
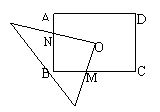
12．（2006泰州）如图，O为矩形ABCD的中心，将直角三角板的直角顶点与O点重合，转动三角板使两直角边始终与BC、AB相交，交点分别为M、N．如果AB=4，AD=6，O M=,ON=
则
与的关系是（ ）
A．
B．
C．
D．
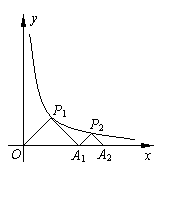
13．(2005年南通)如图，△P1O A1、△P2 A1 A2是等腰直角三角形，点P1、
P2在函数
（x＞０）的图象上，斜边OA1、A1A2都
在x轴上，则点A2的坐标是 
．
14．（2006重庆）如图，矩形AOCB的两边OC、OA分别位于轴、轴上，点B的坐标为（
），D是AB边上的一点.将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图像上，那么该函数的解析式是 ．
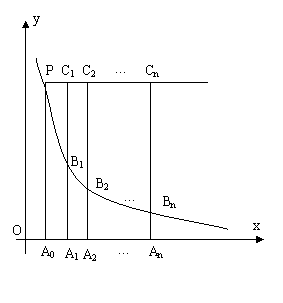15．（2006大连）如图，直线y＝k和双曲线相交于点P，过P点作PA0垂直x轴，垂足为A0，x轴上的点A0、A1、A2、…A n 的横坐标是连续的整数，过点A1、A2、…A n分别作x轴的垂线，与双曲线（x＞0）及直线y＝k分别交于点B1、B2、…B n ，C1、C2、…C n 。
（1）求A0点坐标；
（2）求
及
的值；
（3）试猜想
的值（直接写答案）
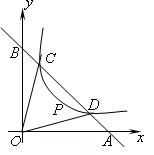
16．(2005梅州市）如图，已知C、D是双曲线
在第一象限分支上的两点，直线CD分别交x轴、y轴于A、B两点。设C（x1，y1）、D（x2，y2），连结OC、OD（O是坐标有点），若∠BOC=∠AOD=α，且tanα=
，OC=
。
（1）求C、D的坐标和m的值；
（2）双曲线上是否存在一点P，使得ΔPOC和ΔPOD的
面积相等？若存在，给出证明，若不存在，说明理由。
反思纠错
1．
已知函数
解：设
，则
上述解法是否正确？为什么？