初三年级第五章反比例函数测试题
姓名 班级
一、填空题：（3分×10=30分）
1、
与
成反比，且当＝8时，
，这个函数解析式为 ；
2、函数
和函数
的图像有 个交点；
3、反比例函数
的图像经过（－
，4）点、（
，－3）及（10，
）点，
则
＝ ，＝ ，＝ ；
4、若反比列函数
的图像经过二、四象限，则= _______
5、已知
-2与
成反比例，当=3时，=1，则与间的函数关系式为
；
6、已知正比例函数
与反比例函数
的图象都过A（
，1），则＝ ，正比例函数的解析式是
。
7、 设有反比例函数
，
、
为其图象上的两点，若
时，
，则的取值范围是___________
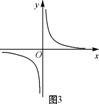
8、如图3是反比例函数
的图象，则k与0的大小关系是k 0.
9、函数
的图像，在每一个象限内，随的增大而 ；
10、已知函数
的图象有两个交点，其中一个交点的横坐标为1，则两个函数图象的交点坐标是 ；
二、选择题： （3分×10=30分）
1、下列函数中，是的反比例函数的是（ ）
A、
B、
C、 
D、
2、已知反比例函数的图像经过点（，），则它的图像一定也经过（ ）
A、 (－,－) B、 (,－)
C、 (－，)
D、（0，0）
3、若与－3成反比例，与
成正比例，则是
的（ ）
A、正比例函数 B、反比例函数 C、一次函数 D、不能确定
4、函数的图象经过点（－4，6），则下列各点中在图象上的是（ ）
A、（3，8） B、（3，－8） C、（－8，－3） D、（－4，－6）
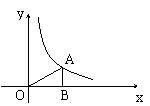5、如上右图，A为反比例函数图象上一点，AB垂直轴于B点，若
＝3，则的值为（ ）
A、6 B、3 C、 D、不能确定
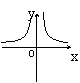
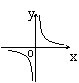
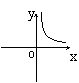
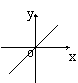
6、如果矩形的面积为6cm2，那么它的长cm与宽cm之间的函数关系用图象表示为（ ）
 | |||||||
 | |||||||
 |  | ||||||
A B C D
7、在同一直角坐标平面内，如果直线
与双曲线
没有交点，那么
和
的关系一定是（ ）
A. +=0 B.
<0 C.
>0 D.=
8、如图 ，A、C是函数
的图象上的任意两点，过A作轴的垂线，垂足为B，过C作y轴的垂线，垂足为D，记RtΔAOB的面积为S1，RtΔCOD的面积为S2则 （ ）
A． S1 ＞S2 B． S1 <S2
C． S1=S2 D． S1与S2的大小关系不能确定
9、已知反比例函数
的图像上有两点A(
，
)，B(
，
)，且
，则
的值是（ ）
A、正数 B、负数 C、非正数 D、不能确定
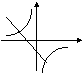
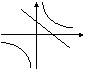
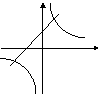
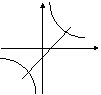10、在同一坐标系中，函数
和
的图像大致是 （ ）
A B C D
三、解答题：（每小题10分，共40分）
1、在某一电路中，保持电压U不变，电流I(安培)与电阻R(欧姆)成反比例，当电阻R=5欧姆时，电流I=2安培。
（1）求I与R之间的函数关系式
（2）当电流I=0.5安培时，求电阻R的值；
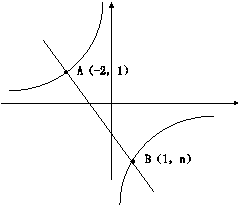2、如图，一次函数
的图像与反比例函数
的图像相交于A、B两点，
（1）利用图中条件，求反比例函数和一次函数的解析式
（2）根据图像写出使一次函数的值大于反比例函数的值的的取值范围。
3、已知
，与
成正比例，
与
成反比例，且当
时，
；当
时，
；求与之间的函数解析式。
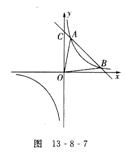
4．如图13－8－7已知一次函数
和反比例函数图象在第一象限内有两个不同的公共点A、B．
（1）求实数的取值范围；（2）若ΔAOB的面积S＝24，求的值．
参考答案：
一、填空题：
1、
2、0
3、- 6，2，
4、0 5、
6、3，
7、k< - 1
8、>
9、增大
10、（1，2）与（-1，-2）
二、选择题：DAAAA CBCDA
三、解答题：
1、（1）
（2）I=0.5时，R=20（欧姆）
2、解：（1）∵过点A（-2，1）
∴m= - 2
∴反比例函数的解析式为
它过点B（1，n）
∴n = - 2
∵过点A（- 2，1）、B（1，- 2）
∴
，解得
∴一次函数与反比例函数的解析式分别为
与
（2）由题意得：当
或
时，一次函数的值大于反比例函数的值。
3、解：设
，
，则
∵时，；当时，.
∴
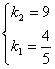
∴y与之间的函数关系式为
4、解：(1)∵的图象在一、三象限
∴k>0
∵与相交
∴
,
∴
∴
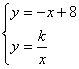有两个不等实根
∴k<16
∴实数k的取值范围为0<k<16
(2) ∵
=32
=32
∴
即
，解得k的值为7.
∴的图像与反比例函数