反比例函数检测（一）
班级_______姓名__________
1.、在下列函数表达式中,x均为自变量,哪些y是x的反比例函数?每一个反比例函数相应的k值是多少?
 |
（9）y=-2x-1
2、.若y=-3xa+1是反比例函数，则a= 。
3.、若y=（a+2）x a2 +2a-1为反比例函数关系式，则a= 。
4、如果反比例函数y=
的图象位于第二、四象限，那么m的范围为
5、下列的数表中分别给出了变量y与x之间的对应关系，其中是反比例函数关系的是
| x | 1 | 2 | 3 | 4 |
| y | 6 | 8 | 9 | 7 |
| x | 1 | 2 | 3 | 4 |
| y | 8 | 5 | 4 | 3 |
| x | 1 | 2 | 3 | 4 |
| y | 5 | 8 | 7 | 6 |
| X | 1 | 2 | 3 | 4 |
| y | 1 | 1/2 | 1/3 | 1/4 |
6、回答下列问题：
（1） 当路程 s 一定时，时间 t 与速度 v 的函数关系。
（2） 当矩形面积 S一定时，长 a 与宽 b 的函数关系。
（3） 当三角形面积 S 一定时，三角形的底边 y 与高 x的函数关系。
（4） 当电压U不变时，通过的电流I与线路中的电阻R的函数关系。
7、实践应用
1、设面积为20cm2的平行四边形的一边长为a（cm），这条边上的高为h（cm），
⑴求h关于a的函数解析式及自变量a的取值范围；
⑵ h关于a的函数是不是反比例函数？如果是，请说出它的比例系数
⑶求当边长a=25cm时，这条边上的高。
2、设电水壶所在电路上的电压保持不变，选用电热丝的电阻为R（Ω），电水壶的功率为P（W）。
(1) 已知选用电热丝的电阻为50 Ω，通过电流为968w，求P关于R的函数解析式，并说明比例系数的实际意义。
(2)如果接上新电热丝的电阻大于50 Ω，那么与原来的相比，电水壶的功率将发生什么变化？
3、（1）y是关于x的反比例函数，当x=-3时，y=0.6；求函数解析式和自变量x的取值范围。
（2）如果一个反比例函数的图象经过点（-2，5），（-5，n）求这个函数的解析式和n的值。
（3）y与x+1成反比例，当x＝2时，y＝－1，求函数解析式和自变量x的取值范围。
(4) 已知y与x-2成反比例，并且当x＝3时，y＝2．求x＝1.5时y的值．
（5）如果
是
的反比例函数，是
的反比例函数，那么是的（ ）
A．反比例函数 B．正比例函数 C．一次函数 D．反比例或正比例函数
反比例函数检测（二）
班级_______姓名__________
1 、 反比例函数y=-
的图象是
，分布在第 象限，在每个象限内， y都随x的增大而
；若 p1 (x1 , y1)、p2 (x2 , y2) 都在第二象限且x1<x2
, 则y1
y2。
3、已知反比例函数 ，若X1 <x2 ,其对应值y1,y2 的大小关系是
4、如图在坐标系中，直线y=x+ k与双曲线 
在第一象限交与点A， 与x轴交于点C，AB垂直x轴，垂足为B，且S△AOB＝1
1）求两个函数解析式
2）求△ABC的面积
6、已知反比例函数的图象经过点
，若一次函数y=x+1的图象平移后经过该反比例函数图象上的点B(2，m)，求平移后的一次函数的图象与x轴的交点坐标。
4、某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20米和11米的矩形大厅内修建一个60平方米的矩形健身房ABCD. 该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为20元/平方米，新建（含装修）墙壁的费用为80元/平方米. 设健身房的高为3米，一面旧墙壁AB的长为x米，修建健身房的总投入为y元.
（1）求y与x的函数关系式；
（2）为了合理利用大厅，要求自变量x必须满足8≤x≤12. 当投入资金为4800元时，问利用旧墙壁的总长度为多少米？
第一章 反比例函数测试卷
基础达标验收卷
一、选择题：
1.
已知反比例函数
的图象经过点
，则函数
可确定为（ ）
A. 
B. 
C.
D.
2.
如果反比例函数的图象经过点
，那么下列各点在此函数图象上的是（ ）
A. 
B.
C.
D.
3.
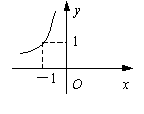如右图，某个反比例函数的图象经过点P，则它的解析式为（ ）
A. 
B.
C. 
D.
4.
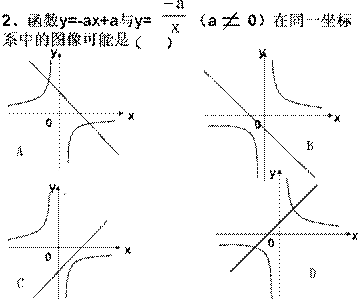
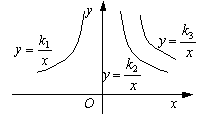如右图是三个反比例函数
，
，
在x轴上方的图象，由此观察得到
、
、
的大小关系为（ ）
A. 
B.
C. 
D.
5.
已知反比例函数
的图象上有两点
、
且
，那么下列结论正确的是（ ）
A. 
B. 
C. 
D
与
之间的大小关系不能确
定
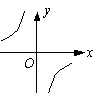6、已知反比例函数的图象如右图，则函数
的图象是下图中的（ ）
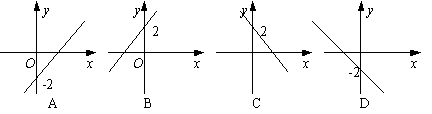
7、已知关于x的函数
和
（k≠0），它们在同一坐标系内的图象大致是（ ）
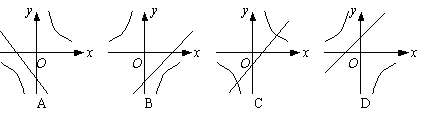
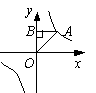8、如图，点A是反比例函数
图象上一点，AB⊥y轴于点B，则△AOB的面积是（ ）
A. 1 B. 2 C. 3 D. 4
9、
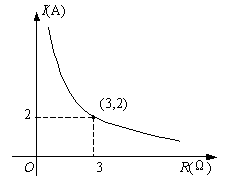某闭合电路中，电源的电压为定值，电流I（A）与电阻R（Ω）成反比例. 右图表示的是该电路中电流I与电阻R之间的图象，则用电阻R表示电流I的函数解析式为（ ）
A. 
B.
C. 
D.
二、填空题：
1.
我们学习过反比例函数. 例如，当矩形面积S一定时，长a是宽b的反比例函数，其函数关系式可以写为
（S为常数，S≠0）.
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例，并写出它的函数关系式.
实例：_________________________________________________；
函数关系式：___________________________________________.
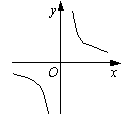
2.
右图是反比例函数的图象，那么k与0的大小关系是
.
3.
点
在双曲线上，则k=______________.
4. 近视眼镜的度数y（度）与镜片焦距x（米）成反比例. 已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数y与镜片焦距x之间的函数关系式是_____________.
5.
已知反比例函数
的图象经过点
，则a=__________.
三、解答题：
1.
已知一次函数
的图象与反比例函数
的图象在第一象限交于点
，求k，n的值.
2.
已知反比例函数的图象与一次函数
的图象相交于点
.
（1）分别求这两个函数的解析式.
（2）试判断点
关于x轴的对称点
是否在一次函数的图象上.
3.
反比例函数的图象经过点
.
（1）求这个函数的解析式；
（2）请判断点
是否在这个反比例函数的图象上，并说明理由.
4. 在压力不变的情况下，某物承受的压强P（Pa）是它的受力面积S（m2）的反比例函数，其图象如右图所示.
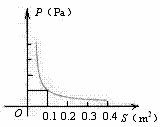（1）求P与S之间的函数关系式；
（2）求当S=0.5m2时物体所受的压强P.
5.
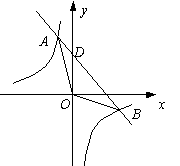如图，反比例函数与一次函数
的图象交于A、B两点.
（1）求A、B两点的坐标；
（2）求△AOB的面积.
能力提高练习
一、学科内综合题
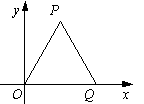
1. 如右图，△OPQ是边长为2的等边三角形，若反比例函数的图象过点P，则它的解析式是_____________.
2.
已知反比例函数
和一次函数
.
（1）若一函数和反比例函数的图象交于点
，求m和k的值.
（2）当k满足什么条件时，这两个函数的图象有两个不同的交点？
（3）当
时，设（2）中的两个函数图象的交点分别为A、B，试判断A、B两点分别在第几象限？∠AOB是锐角还是钝角（只要求直接写出结论）？
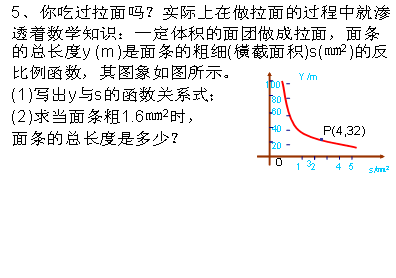
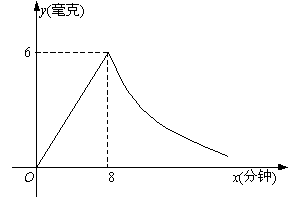3、为了预防“非典”，某学校对教室采用药熏消毒法进行消毒. 已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x分钟）成正比例，药物燃烧完后，y与x成反比例（如图所示）. 现测得药物8分钟燃毕，此时室内空气中每立方米含药量为6毫克. 请根据题中所提供的信息，解答下列问题：
（1）药物燃烧时，y关于x的函数关系式为：___________________，自变量x的取值范围是：______________；药物燃烧后y关于x的函数关系式为：___________________；
（2）研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过几分钟后，学生才能回到教室；
（3）研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效地杀灭空气中的病菌，那么此次消毒是否有效？为什么？