九年级模拟考试数学试卷
试 卷 Ⅰ
一、选择题（本题有10小题，每小题4分，共40分）
1、 －3 + 1的值是（ ）
A、－4 B、－2 C、2 D、4
2、下列实数中，属于无理数的是（ ）
A、0
B、
C、
D、-3
3、如图所示，有一根外观完好无损的木棒长1.6米，其实内部已有0.4米遭虫蚀，如果随机地选一处锯断木棒，所选之处恰好是遭虫蚀的地方概率是（ ）
A、
B、
C、
D、
4、第五次全国人口普查结果显示，我国的总人口已达到1 300 000 000人，用科学记数法表示这个数，结果正确的是（ ）
A、1.3×108 B、1.3×109 C、0.13×1010 D、13×109
5、把抛物线
向左平移一个单位，所得抛物线解析式是（ ）
A、
B、
C、
D、
6、若点P（
）在第二象限，则下列关于m的取值范围正确的是（ ）
|
B、
C、
D、
7、如图所示，当立方体木块A依次向左边移动时，其三视图有变化的是（ ）
A、主视图 B、俯视图
C、左视图 D、都不变化
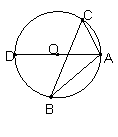
8、如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC=30°。则∠CAD等于（ ）
A、30° B、40° C、50° D、60°
9、如图，矩形ABCD的长、宽分别是5和3，将顶点C折过来，使它落在AB上的C＇（DE为折痕），则CE的长是（ ）
|
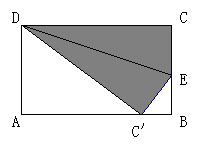A、
B、2 C、
D、
 | |||
| |||
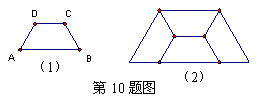
10、如图（1）所示的梯形ABCD，可以经过旋转和轴对称变换形成图（2）所示的梯形.那么梯形ABCD应不具备的性质是（ ）
A、AD=DC=BC B、AB=2CD C、∠A=60° D、∠A=45°
试 卷 Ⅱ
二、填空题（本题有6小题，每小题5分，共30分）
11、如果一个等腰三角形的底角是80°，那么顶角是____________.
12、函数
中自变量x的取值范围为____________.
13、分解因式：
＝ _
____．
|
15、如图，在Rt△ABC中，∠C=90°，CA=CB=2.分别以A、B、C为圆心，以AC为半径画弧，三条弧与边AB所围成的阴影部分的面积是______.
16、在日常生活中，你会注意到有一些含有特殊数学规律的车牌号码，如：浙C80808 、浙C22222、浙C12321等，这些牌照中的五个数字都是关于中间的一个数字“对称”的，给人以对称的美的感受，我们不妨把这样的牌照叫做“数字对称”牌照。如果让你负责制作只以8和9开头且有五个数字的“数字对称”牌照，那么最多可制作 个.
三、解答题：（本题有8小题，共80分）
17、（本题有2小题，每题4分）
（1）计算：
（2）解方程：
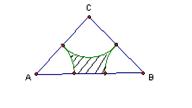
18、（8分）如图，给出下列论断：①DE=CE，②∠1=∠2，③∠3=∠4。请你将其中的两个作为条件，另一个作为结论，构成一个真命题，并加以证明.
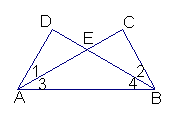条件
结论 （填编号）
证明：
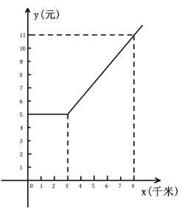19、、（8分）如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题：
(1)当行驶8千米时,收费应为 元
(2)从图象上你能获得哪些信息?(请写出2条)
① ②
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系
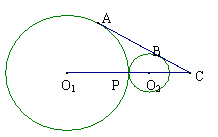20（8分）如图，⊙O1和⊙O2外切于点P，线段AB与⊙O1、⊙O2都相切（A、B为切点），且连心线交于点C，∠ACP=30 °，⊙O1半径为3 cm，⊙O2半径为1 cm，求AB的长.
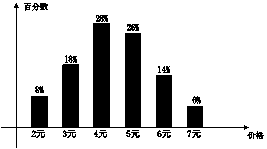
21、（10分）温州某中学为方便学生中午在校就餐，与某饮食服务公司联系为学生供应价格不等的6种盒饭（每人只限一份），。右图是某一天销售情况统计图，条形框上的百分数是销售的该种盒饭占总销售量的百分数，若这一天销售了150份盒饭，
（1）试求出这一天学生购买盒饭所付饭费的平均数和中位数
（2）若饮食服务公司加工各种盒饭的成本如下表所示，这一天的销售中，饮食服务公司共赢利多少元？
| 单价（元） | 2 | 3 | 4 | 5 | 6 | 7 |
| 成本（元） | 1.8 | 2.4 | 3 | 3.8 | 4.2 | 4.5 |
22、作图题：（8分）
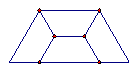
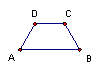（1）如图（1）所示的梯形ABCD，可以经过旋转和轴对称变换形成图（2）所示的梯形.你能看出梯形ABCD应符合什么条件吗？请写出两个符合条件（指边、角的特殊性）
①
②
 |
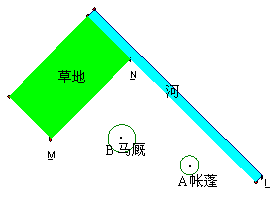
（2）如图，A为马厩，B为帐蓬，牧马人某一天要从马厩牵出马，先到草地边某一处牧马，再
到河边饮马，然后回到帐蓬，请你帮他确定这一
天的最短路线.
23、（14分）初三（2）班的一个综合实践活动小组去A，B两个超市调查去年和今年“五一节”期间的销售情况，下图是调查后小敏与其他两位同学交流的情况.根据他们的对话，请你分别求出A，B两个超市今年“五一节” 期间的销售额.
24．(本小题满分16分)
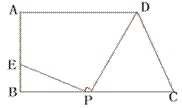
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,在线段BC上任取一点P,连接DP,作射线PE
DP,PE与直线AB交于点E.
(1)试确定CP=3,点E的位置;
(2)若AB=
，设CP=
,BE=
,试写出关于自变量的函数关系式;
(3)在（2）条件下，当点P在CB上移动时，点E会经过点A吗？有几次经过？
(4)请你猜想：线段AB在什么范围内，点E会二次经过点A（只要求结论）
