中考数学模拟试卷二
考试说明:
1、 本试卷分为A卷和第B卷两部分,共30个小题,满分150分,考试时间120分钟.
2、 A卷分为第Ⅰ卷和第Ⅱ卷两部分,答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目准确填涂在答题卡上,请注意答题卡的横竖格式.
3、 第Ⅰ卷选择题共15个小题,选出答案后用铅笔把答题卡上对应题目的答案标号涂黑,若需改动,用橡皮擦擦干净后,再选涂其它答案,不准答在试卷上.
4、 第Ⅱ卷共6个小题,B卷共9个小题,用钢笔或圆珠笔直接答在试卷上,答题前将密封线内的项目填写清楚.
A卷(100分)
第Ⅰ卷 选择题(60分)
一、择题题(每小题4分,在给出的四个选项中,只有一项是符合题目要求的.)
1.下列计算正确的是(a为任何意实数)( )
A.a0
B.a2·a4=a8
C.a4÷2-1
= ![]() a4 D.(a2)3=a6
a4 D.(a2)3=a6
2.下列说法中,正确的是( )
A.![]() π
π![]() 的系数是
的系数是![]() ;
;
B.在(-1)0,cot30°,![]() ,-π-1几个数中,实数有2个;
,-π-1几个数中,实数有2个;
C.若![]() ,则
,则![]() ;
;
D.单项式-xn+1y与单项式2x2n+3y不可能是同类项
3.下列说法正确的是( )
A.近似数1.450有三个有效数字 B.多项式a2b-3b+1是二次三项式
C.0.0109用科学记数法表示为1.09×10-4
 D.
D.![]() 与
与![]() 是同类二次根式
是同类二次根式
4.已知α是锐角,sinα=0.6,则( )
A.0°<α<30° B.30°<α<45°
C.45°<α<60° D.60°<α<90°
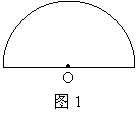
5.对如图1所示的图形的三个说法:
①是半圆;②是弓形;③是扇形,其中正确的个数是( )
A.3 B.2 C.1 D.0
6.一元二次方程x2-ax-2a=0的两根之和为4a-3,则两根之积为( )
A.2 B.-2 C.-6或2 D.6或-2
7.已知直线y=kx+b(k≠0)不经过第三象限,那么k和b的情况分别为( )
A.k>0,b>0 B. k<0,b>0
C. k<0,b≥0
D.k<0,b≤0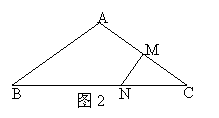
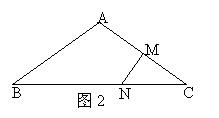
8.如图2,在△ABC中,∠A=120°,
AB=AC,MN垂直平分AC交BC于N,
且NC=4,则BN的长度是( )
A.12 B. 6
C.8 D.10
9.一元二次方程x2-px+q=0的两根分别为1和2,那么x2+px+q因式分解的结果为( )
A.(x-2)(x-1) B.(x-2)(x+1)
C.(x+2)(x-1) D.(x+2)(x+1)
10.直角三角形斜边长10cm,其内切圆的半径为2cm,则它的周长为( )
A.24cm B.22cm C.14cm D.12cm
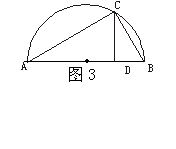
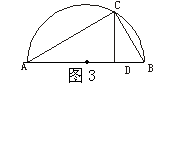 11.如图3所示,AB为半圆的直径,C为
11.如图3所示,AB为半圆的直径,C为
半圆上的一点,CD⊥AB于D,若CD=6,AD:DB
=3:2 ,则AC·BC等于( )
A .![]() B.
B.![]() C.
C.![]() D.90
D.90
12.一组数据6,8,3,6,4,6,5的众数与中位数分别是( )
A.5,6 B.6,6 C.6,5 D.以上答案都不对
13.车轮半径为0.3m的自行车沿着一条直路行驶,车轮绕着轴心转动的转速为100转/分,则自行车的行驶速度为( )
A.3.6πkm/h B.1.8πkm/h C.30km/h D.15km/h
14.若ab<0,则函数y=ax与y= ![]() 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() y
y
y
y
y
y
y
y
 |  |  | |||||
 | |||||||
![]()
![]()
![]()
![]() o x
o
x
o x o
x
o x
o
x
o x o
x
![]()
![]()
![]()
![]()
A B C D
15.梯形的两条对角线互相垂直,其中一条对角线的长是5cm,梯形的高等于4cm,那么梯形的面积是( )
A.25cm2 B.50m2
C.![]() cm2
D.12.5cm2
cm2
D.12.5cm2
第Ⅱ卷(非选择题,40分)
二、解答题:本大题6小题,解答时应写出必要的文字说明,证明过程或演算步骤.
16.(本题满分6分)计算:![]() -sin60°-1-
-sin60°-1-![]() +
+![]() ;
;
17.(本题满分6分)化简求值:![]() ,其中
,其中![]() .
.
18. (本题满分6分)已知方程3x2+5x+1=0的两根为α、β,试求![]() 的值。
的值。
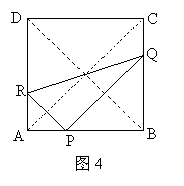
19.(本题满分6分)如图4,正方形ABCD边长为a,通过AB边上一点P作平行于对角线AC,BD的平行线,分别与边BC,AD交于Q和R,设△PQR面积为y,AP为x,问:P在AB上什么位置时,△PQR面积最大?最大面积是多少?
20.(本题满分8分)已知二次函数图像的顶点为P(1,2),且与直线y=2x+k相交于A(2,1).试求:①k值及二次函数的解析式;②该二次函数的图象与直线y=2x+k的另一交点B的坐标及△PAB的面积。
 |
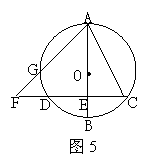 21.(本题满分8分)如图5,已知⊙O的直径AB垂直于弦CD,垂足为E,F为CD延长线上一点,AF交⊙O于点G.求证:AC2=AG·AF.
21.(本题满分8分)如图5,已知⊙O的直径AB垂直于弦CD,垂足为E,F为CD延长线上一点,AF交⊙O于点G.求证:AC2=AG·AF.
B卷(50分)
三、填空题:本大题共6小题,每小题3分,共18分. 将答案填写在对应题号的横线上.
22.将直线y=-2x+6向左平移了3个单位,得到 直线解析式为.
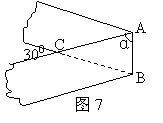
23.如图6,正方形ABCD内接于等腰直角三角形PQR,则![]() =
=
 | |||
 | |||
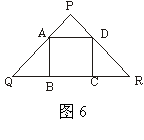
24.如图7,有一条直的等宽纸带,按图7折叠时,纸带重叠部分中的∠α
25.函数y= ![]() +m2-5m+6是正比例函数,则m=
+m2-5m+6是正比例函数,则m=
26.如图8,一个矩形分成4个不同的三角形,绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米,则矩形面积是 平方厘米.
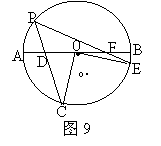
27.如图9,已知AB是⊙O的直径,弦PC交OA于点D,弦PE交OB于点F,且OC=DC,OF=EF,若∠C= ∠E,则∠CPE=
28.(本题满分10分)小明从家到学校上课,开始时以每分钟走50米的速度走了2分钟,这时他发现,若根据以往上学的经验,再按这个速度走下去,将要迟到2分钟,于是他立即加快速度,每分钟多走10米,结果早到2分钟,小时家到学校有多远?
29.(本题满分10分)如图10,地面上有不在同一直线上的A、B、C三点,一只青蛙位于地面异于A、B、C的P点,第一步青蛙从P跳到P关于A的对称点P1,第二步从P1跳到P1关于B的对称点P2,第三步从P2跳到P2关于C的对称点P3,第四步从P3跳到P3关于A的对称点P4……以下跳法类推。问:
(1)青蛙能否跳回到原处P?如果能,请作图并回答至少跳几步回到原处P?
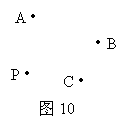 (2)青蛙跳完第2005步落在地面什么位置?
(2)青蛙跳完第2005步落在地面什么位置?
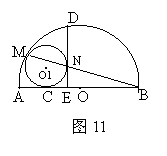
30.(本题满分12分)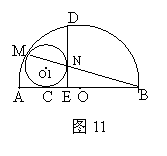 如图11,AB是半圆O的直径,⊙O1与半圆内切于点M,并与AB相切于点C,MB交⊙O1于另一点N,过N作AB的垂线,垂足于E,交半圆于点D。
如图11,AB是半圆O的直径,⊙O1与半圆内切于点M,并与AB相切于点C,MB交⊙O1于另一点N,过N作AB的垂线,垂足于E,交半圆于点D。
求证:(1)BN·BM=BE·BA;(2)BC=BD;(3)DE是⊙O1的切线。
[参考答案]
http://www.DearEDU.com
1.D
2.D
3.D
 4.∵
4.∵![]() <0.6<
<0.6<![]() , ∴sin30°<sinα<sin45°,
, ∴sin30°<sinα<sin45°,
∴30°<α<45°,∴选B.
5.B
6.B,根据根与系数关系,a=4a-3,a=1,所以两之积为-2.
7.C
8.由题意得,∠C=300,MC=![]() ,AC=
,AC=![]() ,推出BC=12,得BN=8,∴选C
,推出BC=12,得BN=8,∴选C
 9.由题意得p=3,q=2,
∴x2+px+q=x2+3x+2=(x+2)(x+1),∴选D.
9.由题意得p=3,q=2,
∴x2+px+q=x2+3x+2=(x+2)(x+1),∴选D.
10.A
11.如图3所示,设AD=3x,则DB=2x,CD2=AD·DB,得x=![]() ,
,
推AB=![]() ,得AC·BC=6×
,得AC·BC=6×![]() =
=![]() ,∴选B.
,∴选B.
12.B
13.计算可知每分钟驶路程为60πm,∴每小时行驶路程为3.6πkm,∴选A.
14.B
15.C
16.![]() -sin60°-1-
-sin60°-1-![]() +
+![]()
=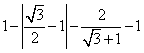 …………..2分
…………..2分
= ![]() …………4分
…………4分
= ![]()
=![]() ……………6分
……………6分
17.![]()
=![]()
= ![]() ……………. 2分
……………. 2分
= ![]()
=![]()
=![]() ……..……..4分
……..……..4分
当x=![]() 时,原式=
时,原式=![]()
= ![]() …………5分
…………5分
=![]() …………..6分
…………..6分
18. ∵α+β=![]() <0,α·β=
<0,α·β=![]() >0
>0
∴α<0,β<0 ………….2分
∴![]() ……….3分
……….3分
=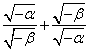 =
= ![]() …………4分
…………4分
=![]() =
= ![]() =
=![]() ………….6分
………….6分
 19.解:∵PQ∥AC,PR∥BD
19.解:∵PQ∥AC,PR∥BD
∴△APR及△PBQ都是等腰直角三角形 ………2分
∵AP=x(0<x<a)
∴梯形ABQR的面积=![]() [x+(a-x)]a=
[x+(a-x)]a=![]() a2
……..3分
a2
……..3分
∴y=![]() -
-![]() [x2+(a-x)2]
[x2+(a-x)2]
=-x2+ax (4分)
=-(x-![]() )2+
)2+![]() …………..5分
…………..5分
 当x=
当x=![]() 时,y取最大值
时,y取最大值![]() ,此时P为AB中点. ………6分
,此时P为AB中点. ………6分
20.解:(1)由已知,可设二次函数的解析式为![]() ,
,
又因为二次函数图象与直线y=2x+k相交于(2,1)
∴![]() ,解之得a=-1
…………….2分
,解之得a=-1
…………….2分
∴二次函数的解析式为y=-(x-1)2+2,即为y=-x2+2x+1
∵y=2x+k过点(2,1)
∴1=4+k
∴k=-3 ………………….3分
![]() (2)解方程组 y=2x-3
(2)解方程组 y=2x-3
y=-x2+2x+1
![]()
![]() 解之,得 x1=2
x2=-2
解之,得 x1=2
x2=-2
y1=1 y2=-7 …………5分
故另一交点坐标为B(-2,-7)
分别过点A,B作AC∥y轴,BC∥x轴,交于点C(如图2)
过点P作PD⊥BC于D ………….6分
∴S△PAB=S△PBD+S四边形PDCA-S△ABC
=![]() ×3×9+
×3×9+![]() (8+9)×1-
(8+9)×1-![]() ×4×8
×4×8
=22-16
=6 ……………8分
21. 如图5
证明:连结AD、CG ………..1分
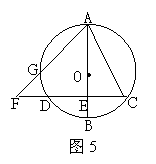 ∵直径AB⊥CD,∴AB平分CD
∵直径AB⊥CD,∴AB平分CD
∴AD=AC, ………….3分
∴∠ADC=∠ACF
∴∠AGC=∠ADC
∵∠ACF=∠AGC …………… 5分
又 ∵∠FAC=∠CAG
∴△ACG∽△ACF ……………6分
∴![]()
∴AC2=AG·AF ……………..8分
B卷(50分)
 22.y=-2(x+3)+6=
-2x-6+6=-2x
22.y=-2(x+3)+6=
-2x-6+6=-2x
| |
24.75°
25.3
26. 21÷(50%-15%)=60
27.40° 如图9,连结PO,则∠CPE=∠C+∠E=2∠C
∠COE=2(∠C+∠E)=4∠C
∠DOC+∠COE+∠EOF=18
所以∠C=20°,即∠CPE=40°
28.解:设小明家到学校的路程为x米,由题可得: …….….1分
![]() .…………..6分
.…………..6分
解得:x=1300(米) ……………9分
答:小明家到学校的路程有1300米. ……………10分

29.解:(1)青蛙能跳回原处P ………..1分
至少跳6步回到原处P作图 …………2分
作图正确 …………..5分
(2)∵2005=334×6+1 …………….8分
∴青蛙跳完第2005步时,落在地面P1处。……10分
 |  | ||||
 | |||||
30.证明:(1)连接AM,
∵AB是半圆O的直径,∴∠BMA=90° ……………2分
又∵DE⊥AB,∠ABM=∠NBE,
∴Rt△ABM∽Rt△NBE
∴![]() ,即BN·BM=BE·BA …………….4分
,即BN·BM=BE·BA …………….4分
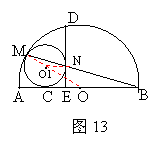
(2)连接AD,BD(如图12),
∵AB是⊙O的直径,∴∠ADB=90° ……………..5分
又因∵DE⊥AB,∴BD2=BE·BA ………………6分
∵BC是⊙O1的切线,∴BC2=BN·BM …………..7分
由(1)知BN·BM=BE·BA,∴BC2=BD2,即BC=BD……..8分
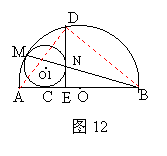
(3)连接O1N和OM(如图13),则OM过点O1,
∵OB=OM,O1N=O1M,∴∠MNO1=∠NMO1=∠MBO ………9分
∴O1N∥OB ………10分
而DE⊥OB,∴OE⊥O1N
∵O1N是 ⊙O1的半径,∴DE是⊙O1的切线. …………12分