中考数学新题型分析（二）
四、图表信息题
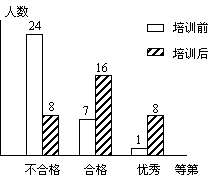1．某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考试考分等级，所绘制的统计图如图所示．试结合图示信息回答下列问题：
（1）这32名学生培训前考分的中位数所在的等级
是 ，培训后考分的中位数所在的等级
是 ．
（2）这32名学生经过培训，考分等级“不合格”
的百分比由 下降到 ．
（3）估计该校整个初二年级中，培训后考分等级为
“合格”与“优秀”的学生共有 名．
（4）你认为上述估计合理吗：理由是什么？
答： ，理由： ．
2．
左图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象（分别为正比例函数和一次函数）．两地间的距离是80千米．请你根据图象回答或解决下面的问题：
（1）谁出发的较早？早多长时间？谁到达乙地较早？
早到多长时间？
（2）两人在途中行驶的速度分别是多少？
（3）请你分别求出表示自行车和摩托车行驶过程的
函数解析式（不要求写出自变量的取值范围）；
（4）指出在什么时间段内两车均行驶在途中（不包
括端点）；在这一时间段内，请你分别按下列条件列
出关于时间x的方程或不等式（不要化简，也不要求
解）：①自行车行驶在摩托车前面；②自行车与摩托车相遇；③自行车行驶在摩托车后面．
五、探索题
1．已知二次函数
的顶点M在直线y=-4x上，并且图象经过点A（-1，0）．
（1）求这个二次函数的解析式；
（2）设此二次函数与x轴的另一个交点为B，与y轴的交点为C，求经过M、B、C三点的圆O′的直径长；
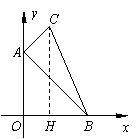（3）设圆O′与y轴的另一个交点为N，经过P（-2，0）、N两点的直线为l，则圆心O′是否在直线l上？请说明理由．
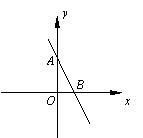
2．Rt△ABC（∠A=90°）在直角坐标系中的位置如图所示，
已知点C（1，4），tg∠CBA=
，tg∠CBO=2．
（1）求点A的坐标及图象过点A、B、C的二次函数解析式．
（2）若（1）中的函数图象与x轴的负半轴交于点P，试判断
△AOP与△ABC是否相似？若相似，请证明；若不相似，请
说明理由．
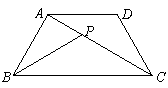3．在等腰梯形ABCD中，AD∥BC，AD<BC，P是对角线AC
上的一点，且∠ABP=∠CAD，AB=4，BC=6．
（1）试找出所有相似的三角形，并分别予以证明；
（2）假设AD=x，BP=y，试求y与x的函数解析式，并写出它
的定义域；
（3）试探索：△ABP是否可能成为等腰三角形？如果可能，请求出此时x的值；如果不可能，请说明理由．
4．已知：如图，梯形ABCD中，AD∥BC，AB=CD=3cm，∠C=60°，BD⊥CD．
（1）求BC、AD的长度；
（2）若点P从点B开始沿BC边向点C以2cm/秒的速
度运动，点Q从点C开始沿CD边向点D以1cm/秒的
速度运动，当P、Q分别从B、C同时出发时，写出五
边形ABPQD的面积S与运动时间t之间的函数关系式，
并写出自变量t的取值范围（不包含点P在B、C两点的情况）；
（3）在（2）的前提下，是否存在某一时刻t，使线段PQ把梯形ABCD分成两部分的面积比为1∶5？若存在，求出t的值；若不存在，请说明理由．
 |