
一、代数应用题:
1、农科所向农民推荐渝江Ⅰ号和渝江Ⅱ号两种新型良种稻谷.在田间管理和土质相同的条件下,Ⅱ号稻谷单位面积的产量比Ⅰ号到谷低20%,但Ⅱ号稻谷的米质好,价格比Ⅰ号高.已知Ⅰ号稻谷国家的收购价是1.6元/千克.
(1) 当Ⅱ号稻谷的国家收购价是多少时,在田间管理、图纸和面积相同的两块田丽分别种植Ⅰ号、Ⅱ号稻谷的收益相同?
(2) 去年小王在土质、面积相同的两块田里分别种植Ⅰ号、Ⅱ号稻谷,且进行了相同的田间管理.收获后,小王把稻谷全部卖给国家.卖给国家时,Ⅱ号稻谷的国家收购价定为2.2元/千克,Ⅰ号稻谷国家的收购价未变,这样小王卖Ⅱ号稻谷比卖Ⅰ号稻谷多收入1040元,那么小王去年卖给国家的稻谷共有多少千克?
[解析] (1)由题意,得![]() (元);
(元);
(2)设卖给国家的Ⅰ号稻谷![]() 千克,根据题意,得
千克,根据题意,得![]() .
.
解得,![]() (千克)
(千克)
![]() (千克)
(千克)
答:(1)当Ⅱ号稻谷的国家收购价是2元时,种植Ⅰ号、Ⅱ号稻谷的收益相同;
(2)小王去年卖给国家的稻谷共为11700千克.
2、机械加工需要拥有进行润滑以减少摩擦,某企业加工一台大型机械设备润滑用油90千克,用油的重复利用率为60%,按此计算,加工一台大型机械设备的实际耗油量为36千克.为了建设节约型社会,减少油耗,该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关.
(1) 甲车间通过技术革新后,加工一台大型机械设备润滑用油量下降到70千克,用油的重复利用率仍然为60%.问甲车间技术革新后,加工一台大型机械设备的实际耗油量是多少千克?
(2) 乙车间通过技术革新后,不仅降低了润滑用油量,同时也提高了用油的重复利用率,并且发现在技术革新的基础上,润滑用油量每减少1千克,用油量的重复利用率将增加1.6%. 这样乙车间加工一台大型机械设备的实际耗油量下降到12千克. 问乙车间技术革新后,加工一台大型机械设备润滑用油量是多少千克?用油的重复利用率是多少?
[解析]
(1)由题意,得![]() (千克)
(千克)
(2)设乙车间加工一台大型机械设备润滑用油量为![]() 千克,
千克,
由题意,得![]()
整理,得![]()
解得:![]() (舍去)
(舍去)
![]()
答:(1)技术革新后,甲车间加工一台大型机械设备的实际耗油量是28千克.
(2)技术革新后,乙车间加工一台大型机械设备润滑用油量是75千克?用油的重复利用率是84%.
3、某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
| 员工 | 管理人员 | 普通工作人员 | |||||
| 人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
| 员工数(名) | 1 | 3 | 2 | 3 |
| 24 | 1 |
| 每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
![]()
![]()
 请你根据上述内容,解答下列问题:
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数![]() 为2500元,
为2500元,
中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作
人员.请你回答右图中小张的
问题,并指出用(2)中的哪个
数据向小张介绍员工的月工资
实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资![]() (结果保留整数),并判断
(结果保留整数),并判断![]() 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.
[解析] (1)由表中数据知有16名;
(2)由表中数据知中位数为1700;众数为1600;
(3)这个经理的介绍不能反映该公司员工的月工资实际水平.
用1700元或1600元来介绍更合理些.
(说明:该问中只要写对其中一个数据或相应统计量(中位数或众数)也可以)
(4)![]() ≈1713(元).
≈1713(元).
![]() 能反映.
能反映.
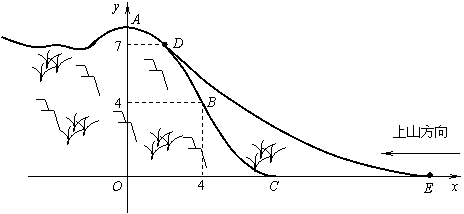
4、某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为![]() ,BC所在抛物线的解析式为
,BC所在抛物线的解析式为![]() ,且已知
,且已知![]() .
.
(1)设![]() 是山坡线AB上任意一点,用y表示x,并求点B的坐标;
是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).
①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一直铺到山脚,为什么?
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,![]() (米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为
(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为![]() .试求索道的最大悬空高度.
.试求索道的最大悬空高度.

[解析] (1)∵![]() 是山坡线AB上任意一点,
是山坡线AB上任意一点,
∴![]() ,
,![]() , (…2分)
, (…2分)
∴![]() ,
,![]() (…3分)
(…3分)
∵![]() ,∴
,∴![]() =4,∴
=4,∴![]() (…4分)
(…4分)
(2)在山坡线AB上,![]() ,
,![]()
①令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]()
∴第一级台阶的长度为![]() (百米)
(百米)![]() (厘米) (…6分)
(厘米) (…6分)
同理,令![]() 、
、![]() ,可得
,可得![]() 、
、![]()
∴第二级台阶的长度为![]() (百米)
(百米)![]() (厘米) (…7分)
(厘米) (…7分)
第三级台阶的长度为![]() (百米)
(百米)![]() (厘米) (…8分)
(厘米) (…8分)
②取点![]() ,又取
,又取![]() ,则
,则![]()
∵![]()
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚 (…10分)
(注:事实上这种台阶从山顶开始最多只能铺到700米高度,共500级.从100米高度到700米高度都不能铺设这种台阶.解题时取点具有开放性)
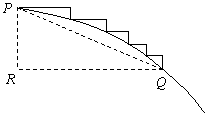 ②另解:连接任意一段台阶的两端点P、Q,如图
②另解:连接任意一段台阶的两端点P、Q,如图
∵这种台阶的长度不小于它的高度
∴![]()
当其中有一级台阶的长大于它的高时,
![]() (…9分)
(…9分)
在题设图中,作![]() 于H
于H
则![]() ,又第一级台阶的长大于它的高
,又第一级台阶的长大于它的高
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚 (…10分)
 (3)
(3)
![]() 、
、![]() 、
、![]() 、
、![]()
由图可知,只有当索道在BC上方时,索道的悬空高度才有可能取最大值(…11分)
索道在BC上方时,悬空高度![]()
![]()
![]()
![]() (…13分)
(…13分)
当![]() 时,
时,![]()
∴索道的最大悬空高度为![]() 米.
米.
5、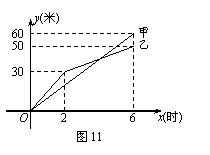 有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.图11是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:
有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.图11是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:
(1)乙队开挖到30米时,用了_____小时.开挖6小时时,
甲队比乙队多挖了______米;
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数关系式;
②乙队在2≤x≤6的时段内,y与x之间的函数关系式;
③开挖几小时后,甲队所挖掘河渠的长度开始超过乙队?
(3)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.问甲队从开挖到完工所挖河渠的长度为多少米?
[解析] (1)2;10;
(2)①设甲队在0≤x≤6的时段内y与x之间的函数关系式为y=k1x,
由图可知,函数图象过点(6,60),
∴6 k1=60,解得k1=10,
∴y =10x.
②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y =k2x+b,
由图可知,函数图象过点(2,30)、(6,50),
∴![]() 解得
解得![]()
∴y =5x+20.
③由题意,得10x>5x+20,解得x>4.
所以,4小时后,甲队挖掘河渠的长度开始超过乙队.
(说明:通过观察图象并用方程来解决问题,正确的也给分)
(3)由图可知,甲队速度是:60÷6=10(米/时).
设甲队从开挖到完工所挖河渠的长度为z米,依题意,得
![]()
解得 ![]() =110.
=110.
答:甲队从开挖到完工所挖河渠的长度为110米.
6、利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的二次函数关系式(不要求写出x的取值范围);
(3)请把(2)中的二次函数配方成![]() 的形式,并据此说明,该经销店要
的形式,并据此说明,该经销店要
获得最大月利润,售价应定为每吨多少元;
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
[解析] (1)![]() =60(吨).
=60(吨).
(2)![]() ,
,
化简得: ![]() .
.
(3)![]()
![]() .
.
利达经销店要获得最大月利润,材料的售价应定为每吨210元.
(4)我认为,小静说的不对.
理由:方法一:当月利润最大时,x为210元,
而对于月销售额![]()
![]() 来说,
来说,
当x为160元时,月销售额W最大.
∴当x为210元时,月销售额W不是最大.
∴小静说的不对.
方法二:当月利润最大时,x为210元,此时,月销售额为17325元;
而当x为200元时,月销售额为18000元.∵17325<18000,
∴当月利润最大时,月销售额W不是最大.
∴小静说的不对.
(说明:如果举出其它反例,说理正确,也相应给分)
二、几何应用题:
8、图10—1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图10—2是车棚顶部截面的示意图,![]() 所在圆的圆心为O.
所在圆的圆心为O.
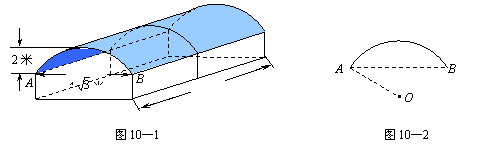 |
车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留
[解析]![]()
连结OB,过点O作OE⊥AB,垂足为E,交![]() 于F,如图1. …………(1分)
于F,如图1. …………(1分)
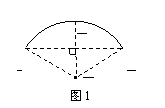 由垂径定理,可知: E是AB中点,F是
由垂径定理,可知: E是AB中点,F是![]() 中点,
中点,
∴EF是弓形高 .
∴AE=![]() 2
2![]() ,EF=2. …………(2分)
,EF=2. …………(2分)
设半径为R米,则OE=(R-2)米.
在Rt△AOE中,由勾股定理,得 R 2=![]() .
.
解得 R =4. ……………………………………………………………………(5分)
∵sin∠AOE=![]() , ∴ ∠AOE=60°, ………………………………(6分)
, ∴ ∠AOE=60°, ………………………………(6分)
∴∠AOB=120°. ∴
![]() 的长为
的长为![]() =
=![]()
![]() . ………………………(7分)
. ………………………(7分)
∴帆布的面积为![]()
![]() ×60=160
×60=160![]() (平方米). …………………………………(8分)
(平方米). …………………………………(8分)
(说明:本题也可以由相交弦定理求圆的半径的长.对于此种解法,请参照此评分标准相应给分)
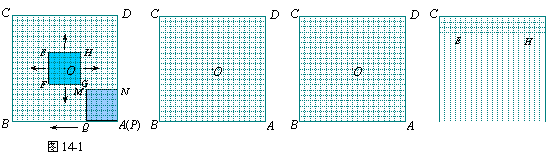
9、图14-1至图14-7的正方形霓虹灯广告牌ABCD都是20×20的等距网格(每个小方格的边长均为1个单位长),其对称中心为点O.
如图14-1,有一个边长为6个单位长的正方形EFGH的对称中心也是点O,它以每秒1个单位长的速度由起始位置向外扩大(即点O不动,正方形EFGH经过一秒由6×6扩大为8×8;再经过一秒,由8×8扩大为10×10;……),直到充满正方形ABCD,再以同样的速度逐步缩小到起始时的大小,然后一直不断地以同样速度再扩大、再缩小.
另有一个边长为6个单位长的正方形MNPQ从如图14-1所示的位置开始,以每秒1个单位长的速度,沿正方形ABCD的内侧边缘按A→B→C→D→A移动(即正方形MNPQ从点P与点A重合位置开始,先向左平移,当点Q与点B重合时,再向上平移,当点M与点C重合时,再向右平移,当点N与点D重合时,再向下平移,到达起始位置后仍继续按上述方式移动).
正方形EFGH和正方形MNPQ从如图14-1的位置同时开始运动,设运动时间为x秒,它们的重叠部分面积为y个平方单位.
(1)请你在图14-2和图14-3中分别画出x为2秒、18秒时,正方形EFGH和正方形MNPQ的位置及重叠部分(重叠部分用阴影表示),并分别写出重叠部分的面积;
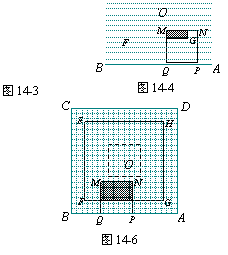
(2)①如图14-4,当1≤x≤3.5时,求y与x的函数关系式;
②如图14-5,当3.5≤x≤7时,求y与x的函数关系式;
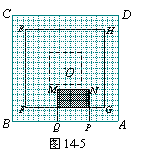
③如图14-6,当7≤x≤10.5时,求y与x的函数关系式;
④如图14-7,当10.5≤x≤13时,求y与x的函数关系式.
(3)对于正方形MNPQ在正方形ABCD各边上移动一周的过程,请你根据重叠部分面积y的变化情况,指出y取得最大值和最小值时,相对应的x的取值情况,并指出最大值和最小值分别是多少.(说明:问题(3)是额外加分题,加分幅度为1~4分)
 | |||
| |||
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 | |||||||
| |||||||
 | |||||||
[解析]![]()
(1)相应的图形如图2-1,2-2.
当x=2时,y=3;
 当x=18时,y=18.
当x=18时,y=18.
 |
(2)①当1≤x≤3.5时,如图2-3,
延长MN交AD于K,设MN与HG交于S,MQ与FG交于T,则MK=6+x,SK=TQ=7-x,从而MS=MK-SK=2x-1,MT=MQ-TQ=6-(7-x)= x-1.
∴y=MT·MS=(x-1)(2x-1)=2x2-3x+1.
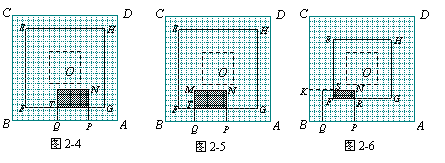
②当3.5≤x≤7时,如图2-4,设FG与MQ交于T,则
TQ=7-x,∴MT=MQ-TQ=6-(7-x)=x-1.
∴y=MN·MT=6(x-1)=6x-6.
③当7≤x≤10.5时,如图2-5,设FG与MQ交于T,则
TQ=x-7,∴MT=MQ-TQ=6-(x-7)=13-x.
∴y= MN·MT =6(13-x)=78-6x.
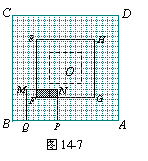
④当10.5≤x≤13时,如图2-6,设MN与EF交于S,NP交FG于R,延长NM交BC于K,则MK=14-x,SK=RP=x-7,
∴SM=SK-MK=2x-21,从而SN=MN-SM=27-2x,NR=NP-RP=13-x.
∴y=NR·SN=(13-x)(27-2x)=2x2-53x+351.
(说明:以上四种情形,所求得的y与x的函数关系式正确的,若不化简不扣分)
(3)对于正方形MNPQ,
 ①在AB边上移动时,当0≤x≤1及13≤x≤14时,y取得最小值0;
①在AB边上移动时,当0≤x≤1及13≤x≤14时,y取得最小值0;
当x=7时,y取得最大值36.
②在BC边上移动时,当14≤x≤15及27≤x≤28时,y取得最小值0;
当x=21时,y取得最大值36.
③在CD边上移动时,当28≤x≤29及41≤x≤42时,y取得最小值0;
当x=35时,y取得最大值36.
④在DA边上移动时,当42≤x≤43及55≤x≤56时,y取得最小值0;
当x=49时,y取得最大值36.