九年级数学《圆》单元测试卷
一、仔细选一选（每小题3分，共30分）
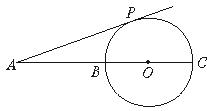
1、如图1,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于______时,AC才能成为⊙O的切线.
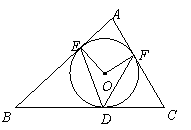
2、如图2，⊙O内切于
，切点分别为
．已知
，
，连结
，那么
等于
3、如图3，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为 ⊙O的直径，AD=6，则BC＝ 。
 |
图1 图2 图3 图4
4、如图4，△ABC为⊙O的内接三角形，O为圆心. OD⊥AB，垂足为D，OE⊥AC，垂足为E，若DE＝3，则BC＝ .
5、如图5，⊙O内切于，切点分别为．已知，，连结，那么等于
6、如图6,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于______时,AC才能成为⊙O的切线.
7、如图7，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为
⊙O的直径，AD=6，则BC＝
。
 |
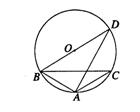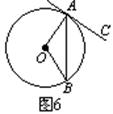
图5 图7 图8
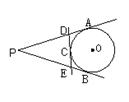
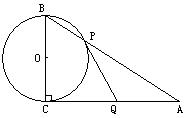
8.如图8所示,PA与PB分别切⊙O于A、B两点,C是弧AB上任意一点,过C作⊙O的切线,交PA及PB于D、E两点,若PA=PB=5cm,则△PDE的周长是_______cm.
9．如图，已知∠AOB=30°，M为OB边上任意一点，以M为圆心，2cm为半径作⊙M，当OM=______cm时，⊙M与OA相切．
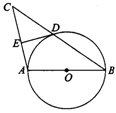
10、如图，BC为半⊙O的直径，点D是半圆上一点，过点D作⊙O的切线AD，BA⊥DA于A，BA交半圆于E，已知BC=10，AD=4，那么直线CE与以点O为圆心，
为半径的圆的位置关系是________．
9题图 10题图
二、 选择题（每小题3分，共27分）
1.I为△ABC的内心,如果∠ABC+∠ACB=100°,那么∠BIC等于( )
A.80° B.100° C.130° D.160°
2.⊙O的半径为6,⊙O的一条弦AB长为3
,以3为半径的同心圆与直线AB 的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
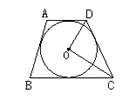
3.如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( )
A.70° B.90° C.60° D.45°
4．如图，BC是⊙O直径，点A为CB延长线上一点，AP切⊙O于点P，若AP=12，
AB∶BC=4∶5，则⊙O的半径等于 （ ）
A．4 B．5 C．6 D．7
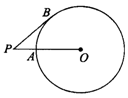
5、如图PB为⊙O的切线，B为切点，连结PO交⊙O于点A，PA=2，PO=5，则PB的长度为（ ）
A．4
B．
C．2
D．4
3题图 4题图 5题图
6．P是⊙O外一点，PA、 PB切⊙O于点A、B，Q是优弧AB上的一点，设∠APB=α，∠AQB=β ，则α与β的关系是
A．α=β B．α+β=90° C．α+2β=180° D．2α+β=180°
7．直线L上的一点到圆心的距离等于⊙O的半径，则L与⊙O的位置关系是
A．相离 B．相切 C．相交 D．相切或相交
8．圆的最大的弦长为12 cm，如果直线与圆相交，且直线与圆心的距离为d，那么
A．d<6 cm B． 6 cm<d<12 cm C．d≥6 cm D． d>12 cm
9、已知⊙O的半径为r，圆心O到直线L的距离为d，若直线L与⊙O有交点，则下列结论中正确的是（ ）
A．d=r B．d≤r C．d≥r D．d>r
三、 解答题（分，请同学们注意做题步骤）
1、如图，在△ABC中，∠BCA =90°，以BC为直径的⊙O交AB于点P，Q是AC的中点．判断直线PQ与⊙O的位置关系，并说明理由．（10分）
2、如图，已知∠C = 900，点O在AC上，CD为⊙O直径，⊙O切AB于E，若BC =5
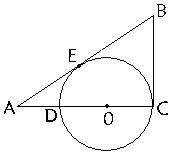AC = 12，求⊙O的半径。（10分）
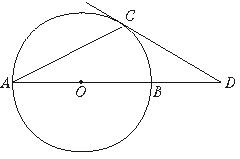
3．如图9，AB是⊙O的直径，点D在AB的延长线上，且BD=OB，点C在⊙O上，
∠CAB=30°，求证：DC是⊙O的切线．(10分)
4．已知在Rt△ABC中，∠C=90°，AD是∠BAC的角平分线，以AB上一点O为圆心，AD为弦作⊙O．（1）在图中作出⊙O；（不写作法，保留作图痕迹）（5分）
（2）求证：BC为⊙O的切线；（8分）
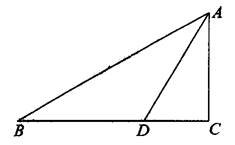
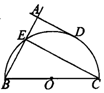
5、如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙O′交
轴于D点，过点D作DF⊥AE于点F．
（1）求OA、OC的长；（6分）
（2）求证：DF为⊙O′的切线；（8分）
（3）小明在解答本题时，发现△AOE是等腰三角形．由此，他断定：“直线
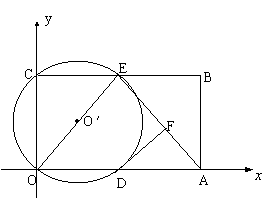BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”．你同意他的看法吗？请充分说明理由．（6分）