![]()
 初三年级数学月考试卷
初三年级数学月考试卷
数 学
(时间120分钟 满分100分)
一、选择题:(每小题3分,共24分. 每小题四个选项,只有一项是正确的,请把它填写在答题卷上.)
1.下列计算错误的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() .
.
2.在函数![]() 中,自变量
中,自变量![]() 的取值范围是
( )
的取值范围是
( )
A.![]() 且
且![]() B.
B.![]() 且
且![]() C.
C.![]() D.
D.![]()
3.已知甲乙两组数据的平均数都是5,甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() 则( )
则( )
A.甲组数据比乙组数据的波动大 B.乙组数据比甲组数据的波动大
C.甲组数据与乙组数据的波动一样大 D.甲乙两组数据的波动大小不能比较
4.用M,N,P,Q各代表四种简单几何图形(线段、正三角形、正方形、圆)中的一种.
图4-1—图4-4是由M,N,P,Q中的两种图形组合而成的(组合用“&”表示).
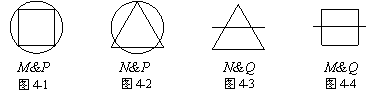 |
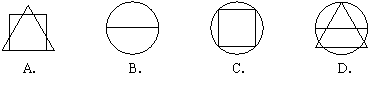
那么,下列组合图形中,表示P&Q的是 ( )
 |
5. 方程![]() 的一个解必是
( )
的一个解必是
( )
 A.
A.![]() =-1 B.
=-1 B. ![]() =1 C.
=1 C. ![]() =
=![]() D.
D. ![]() =
=![]()
6.为了弘扬雷锋精神,某中学准备在校园内建造一座
高2m的雷锋人体雕像,向全体师生征集设计方案.小
兵同学查阅了有关资料,了解到黄金分割数常用于人体
雕像的设计中.如图是小兵同学根据黄金分割数设计的
雷锋人体雕像的方案,其中雷锋人体雕像下部的设计高
度(精确到0.01m,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,
![]() ≈2.236)是
( )
≈2.236)是
( )
A、0.62m B、0.76m C、1.24m D、1.62m
7. 在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码.有一种密码,将英文26个字母![]() ,…,
,…,![]() (不论大小写)依次对应1,2,3,…,26这26个自然数(见表格).当明码对应的序号
(不论大小写)依次对应1,2,3,…,26这26个自然数(见表格).当明码对应的序号![]() 为奇数时,密码对应的序号
为奇数时,密码对应的序号![]() ;当明码对应的序号
;当明码对应的序号![]() 为偶数时,密码对应的序号
为偶数时,密码对应的序号![]() .
.
| 字母 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 序号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
按上述规定,将明码“love”译成密码是 ( )
A.gawq B.shxc C.sdri D.love
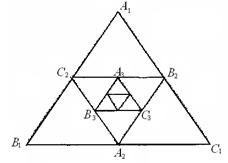 8. 如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积。然后分别取△A1B1C1的三边中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积。用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积……,由此可得,第10个正△A10B10C10的面积是
( )
8. 如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积。然后分别取△A1B1C1的三边中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积。用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积……,由此可得,第10个正△A10B10C10的面积是
( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
二、填空题(第9、10两题各4分,第11-14每小题3分,共20分.请把答案填写在答题卷上.)
9. 计算:![]() __ , 5-
__ , 5-![]() 的整数部分是_____________ .
的整数部分是_____________ .
 10. 已知
10. 已知![]() ,
,![]() ,
,![]() ,若
,若![]() ,(a、b为正整数),请推测a、b的最小值为a=_________,b=__________.
,(a、b为正整数),请推测a、b的最小值为a=_________,b=__________.
11. 化简:![]() =_______________.
=_______________.
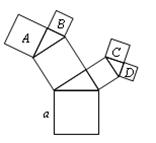
12.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,
其中最大的正方形边长是a,则图中四个小正方形A、B、C、D的面积之和是________________.
13. 若一个三角形的三边长均满足方程![]() ,则此三角形的周长为_______________.
,则此三角形的周长为_______________.
14.若![]() 为整数,关于
为整数,关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则整数k的最大值为__________________.
有实数根,则整数k的最大值为__________________.
![]()
 数 学 答 题 卷
数 学 答 题 卷
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
| 得 分 | 评 卷 人 |
一、选择题:(每小题3分,共24分.每小题四个选项只有一项是正确的,请把它选出来填在答题卷上.)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 得 分 | 评 卷 人 |
二、填空题(第9、10两题各4分,第11-14每小题3分,共20分.请把答案填写在答题卷的横线上.)
9、__________________ 10、____________________ 11、____________________
14、____________________13、____________________ 14、____________________
| 得 分 | 评 卷 人 |
三、解答题(本大题共56分.)
15.(每小题4分,本题共8分)解答下列各题:
(1)计算:![]() .
.
(2)先化简,再求值:![]() ,其中
,其中![]() ,
,![]() .
.
16.(6分)用适当的方法解一元二次方程:
(1)![]() (2)
(2)![]()
17.(6分)某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
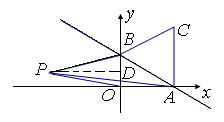
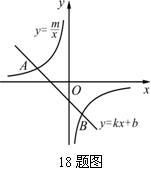 18. (6分) 如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数
18. (6分) 如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1) 求此反比例函数和一次函数的解析式;
(2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
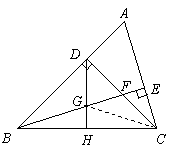
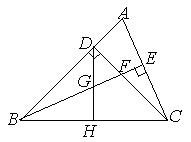 19. (8分)已知:如图,
19. (8分)已知:如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]() 是
是![]() 边的中点,连结
边的中点,连结![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;(3分)
;(3分)
(2)求证:![]() ;(3分)
;(3分)
(3)![]() 与
与![]() 的大小关系如何?试证明你的结论.(2分)
的大小关系如何?试证明你的结论.(2分)
(第19题图)
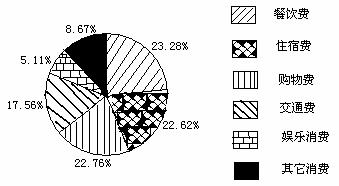
20. (6分)据2007年5月8日《大江晚报》报道:今年“五一”黄金周期间,我市实现旅游收入再创历史新高,旅游消费呈现多样化,各项消费所占的比例如图所示,其中住宿消费为3438.24万元.(1)求我市今年“五一”黄金周期间旅游消费共多少亿元?旅游消费中各项消费的中位数是多少万元?
(2)对于“五一”黄金周期间的旅游消费,如果我市2007年要达到3.42亿元的目标,那么,2007年到2009年的平均增长率是多少?
2007年我市“五一”黄金周旅游各项消费分布统计图
21.(6分)如图21,在平面直角坐标系中,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求![]() 的度数.
的度数.
(2)求过![]() 两点的直线解析式.(计算结果要求分母有理化.参考资料:把分母中的根号化去,叫分母有理化.例如:①
两点的直线解析式.(计算结果要求分母有理化.参考资料:把分母中的根号化去,叫分母有理化.例如:①![]() ;
;
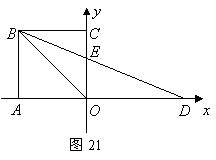 ②
②![]() ;③
;③![]() 等运算都是分母有理化)
等运算都是分母有理化)
22.(10分) 如图22,一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,
轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,
(1) 求△ABC的面积;
(2) 如果在第二象限内有一点P(![]() ),试用含
),试用含![]() 的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时
的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时![]() 的值;
的值;
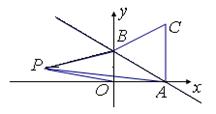 (3) 在
(3) 在![]() 轴上,存在这样的点M,使△MAB为等腰三角形.请直接写出所有符合要求的点M的坐标.
轴上,存在这样的点M,使△MAB为等腰三角形.请直接写出所有符合要求的点M的坐标.
(第22题图)
参 考 答 案
一、选择题:(每小题3分,共24分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| D | A | B | B | B | C | B | A |
二、填空题(第9、10题每小题4分,第11-14题每小题3分,共20分)
9、![]() ,2 ; 10、8, 63; 11、
,2 ; 10、8, 63; 11、![]() ;
12、
;
12、![]() ; 13、6,10,12; 14、3.
; 13、6,10,12; 14、3.
三、解答题(共56分)
15.(1)解:原式=![]() …………………………………………2分
…………………………………………2分
=![]() …………………………………………………………3分
…………………………………………………………3分
=![]() …………………………………………………………4分
…………………………………………………………4分
(2)解: 原式![]() ································································ 1分
································································ 1分
![]() ··········································································· 2分
··········································································· 2分
![]() ········································································································ 3分
········································································································ 3分
当![]() ,
,![]() 时,
时,
原式![]() ·························································· 4分
·························································· 4分
16.
(1)![]() ························································································ 3分
························································································ 3分
(2) ![]() ··························································································· 6分
··························································································· 6分
17.解:设南瓜亩产量的增长率为![]() ,则种植面积的增长率为
,则种植面积的增长率为![]() .································· 1分
.································· 1分
根据题意,得
![]() .············································································ 3分
.············································································ 3分
化简得![]() ································································································· 4分
································································································· 4分
解这个方程,得![]() ,
,![]() (不合题意,舍去).·············································· 5分
(不合题意,舍去).·············································· 5分
答:南瓜亩产量的增长率为![]() .··············································································· 6分
.··············································································· 6分
18.(1) ∵ 点A(-4,2)和点B(n,-4)都在反比例函数y=![]() 的图象上,
的图象上,
∴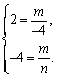 解得
解得![]()
又由点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上,
∴![]() 解得
解得![]()
∴ 反比例函数的解析式为![]() ,一次函数的解析式为y=-x-2 . ………………………4分
,一次函数的解析式为y=-x-2 . ………………………4分
说明:两解析式出现一个错误即不给分 .
(2) x的取值范围是x>2或-4<x<0 . …………………………………………………………6分
19.(1)证明:![]() ,
,![]() ,
,
![]() 是等腰直角三角形.
是等腰直角三角形.
![]() . ………………………………………1分
. ………………………………………1分
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
且![]() ,
,
![]() .
.
又![]() ,
,![]() ,
,
![]() .
.
![]() .………………………………………………………………………………………3分
.………………………………………………………………………………………3分
(2)证明:在![]() 和
和![]() 中
中
![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
又由(1),知![]() ,
,
![]() .……………………………………………………………………………6分
.……………………………………………………………………………6分
(3)![]() .
.
证明:连结![]() .
.
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() .
.
又![]() 是
是![]() 边的中点,
边的中点,
![]() 垂直平分
垂直平分![]() .
.
![]() .………………………………………………………………………………………7分
.………………………………………………………………………………………7分
在![]() 中,
中,
![]() 是斜边,
是斜边,![]() 是直角边,
是直角边,
![]() .
.
![]() . …………………………………………………………………………………8分
. …………………………………………………………………………………8分
20. 解: (1)由图知,住宿消费为3438.24万元,占旅游消费的22.62%,
∴旅游消费共3438.24÷22.62%=15200(万元)=1.52(亿元). …………………………1分
交通消费占旅游消费的17.56%,∴交通消费为15200×17.56%=2669.12(万元).
∴今年该市“五一”黄金周旅游消费中各项消费的中位数是
(3438.24+2669.12)÷2=3053.68(万元). ………………………………………2分
(2)解:设2007年到2009年旅游消费的年平均增长率是![]() , …………………………………3分
, …………………………………3分
由题意,得
![]() ,
,
解得 ![]() ,
,![]() …………………………………………………………5分
…………………………………………………………5分
因为增长率不能为负,故![]() 舍去. ∴
舍去. ∴![]() =0.5=50%.
=0.5=50%.
答:2005年到2007年旅游消费的年平均增长率是50%. …………………………………………6分
21.(1)∵![]() ∴
∴![]()
由正方形![]() 可知,
可知,![]() ∥
∥![]() ,∴
,∴![]()
∴![]()
∴![]() ………………………………………2分
………………………………………2分
(2)设过B、D两点的直线解析式为![]() ……………………………………………3分
……………………………………………3分
∵B(-1,1),D(![]() ,0)
,0)
![]()
![]()
∴![]()
![]()
解得,![]() ……………………………………………………………5分
……………………………………………………………5分
所以所求直线BD的解析式为![]() . ……………………………………6分
. ……………………………………6分
22.解:根据条件,A、B两点的坐标分别是(![]() )、(
)、(![]() ).
).
(1) 在△ABO中,由勾股定理,得![]() ,正△ABC的高是
,正△ABC的高是![]() .
.
所以从而△ABC的面积是![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅2分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅2分
(2) 过P作PD垂直OB于D,则四边形ABPO的面积
![]() . ┅┅┅┅┅┅┅┅4分
. ┅┅┅┅┅┅┅┅4分
当△ABP的面积与△ABC的面积相等时,
四边形ABPO的面积-△AOP的面积=△ABC的面积,
即![]() .
.
解得![]() . ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
. ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分
(3) 符合要求的点M的坐标分别是(![]() )、(
)、(![]() )、(
)、(![]() )、(
)、(![]() ).
).
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅10分