|
1、某几何体的三视图如右图所示，那么
该几何体是 .
2、方程(x＋1)(x－2)＝0的根是 ．
3、某种冰箱进价为x元，按进价增加20％销售，后来因产品更新，又以售价的90％削降处理，现在每台冰箱还有 元利润。
4、△ABC中，D、E、F分别是三边的中点，△ABC的周长为30 cm，则△DEF的周长为 cm.
5、在平行四边形ABCD中，若∠A+∠C=
，则∠A=
∠B=
6、已知方程
的一个根为
，则k=
.
7、在同一时刻，身高1.6米的小强影长1.2米，旗杆影长15米，则旗杆高为
8、等腰直角三角形斜边上的中线长为4cm，则其面积为 。
9、如图，为了求出湖两岸A、B两点之间的距离，观测者从测点A、B分别测得∠BAC＝90°，∠ABC＝30°，又量得BC＝160 m，则A、B两点之间的距离为 m（结果保留根号）。
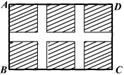
10、如图所示，某小区规划在一个长为40 m、宽为26 m的矩形场地ABCD上修建三条同样宽的甬路，使其中两条与AB平行，另一条与AD平行，其余部分种草.若使每一块草坪的面积为144 m2，求甬路的宽度. 若设甬路的宽度为x m，则x满足的方程为 .
二、 选择题：（每小题4分，共24分）
11、一元二次方程
的根是（ ）A、x=3 B、x=4 C、x1=3，x2=－3 D、x1=
x2=－
12、已知等腰三角形的一个底角等于30°，则这个等腰三角形的顶角等于（ ）
A.150° B.120° C.75° D.30°
13、下列命题中错误的 ( )
A、 平行四边形的对角线互相平分；B、一组对边平行，一组对角相等的四边形是平行四边形；
C、 等腰梯形的对角线相等； D、四边都相等的四边形是正方形.
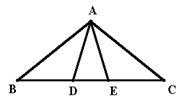14、△ABC中，AB=AC，
ABC＝36
，D、E是BC上的点，BAD＝DAE＝EAC，则图中等腰三角形的个数是
（ ）
A、2个 B、3个 C、4个 D、6个
15、已知菱形的两条对角线长分别为4cm和10cm，则菱形的边长为（ ）
A.116cm B.29cm C.
cm D.
cm
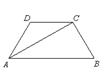
16、如图，在等腰梯形ABCD中，AB∥CD， 对角线AC平分∠BAD，∠B＝60º，CD＝2cm，则梯形ABCD的面积为（
）cm2．A．
B．6 C．
D．12
三、解答题：（17题每题6分,18题8分,19题8分，共28分）
17、解方程：①
.
② (x-3)2=2(x-3)
18、如图，在
中，
是
上一点，
交
于点
，
，
，
与
有什么位置关系？证明你的结论．
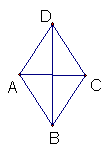
19、已知：菱形ABCD的对角线AC=6m，周长是20m，求另一条对角线BD
的长及菱形的面积。
四、应用题（20题8分，21题9分，共17分）
20、今年，我国政府为减轻农民负担，决定在5年内免去农业税.某乡今
年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两
年降低的百分率相同.
（1）求降低的百分率；
（2）若小红家有4人，明年小红家减少多少农业税？
（3）小红所在的乡约有16000农民，问该乡农民明年减少多少农业税.
 |
21、某商店进了一批服装，进货单价为50元，如果按每件60元出售，可销售800件，如果每件提价1元出售，其销售量就减少20件。
（1）如果设这种服装销售单价为x（x>60）元，请用代数式表示每件的利润及销售的数量。
（2）如果要获利12000元，求出销售单价是多少？
（3）在（2）的前提下，要使销售成本不超过24000元，问这种服装销售单价确定多少为宜？这时应进多少服装？
五、开放探索题（22题9分，23题12分，共21分）
22、将平行四边形纸片ABCD按如图方式折叠，使点C与A重合，点D落到D′ 处，折痕为EF．
（1）求证：△ABE≌△AD′F；
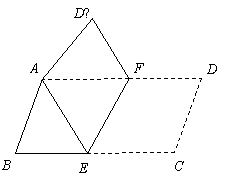（2）连接CF，判断四边形AECF是什么特殊四边形？证明你的结论．
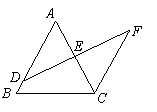
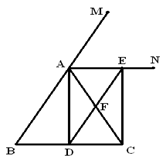
23、已知：如图，在△ABC中，AB＝AC，AD
BC，垂足为D，AN是△ABC外角CAM的平分线，CEAN，垂足为E，连接DE交AC于F
（1）求证：四边形ADCE为矩形
（2）线段DF与AB有怎样的位置关系和数量关系，并说明理由。
（3）当△ABC满足什么条件时，四边形ADCE是一个正方形？简述你的理由。
