第二章 二次函数
一、选择题（共30分）
1.在下列关系式中,y是x的二次函数的关系式是 ( )
A.2xy+x2=1 B.y2-ax+2=0 C.y+x2-2=0 D.x2-y2+4=0
2.设等边三角形的边长为x(x>0），面积为y，则y与x的函数关系式是( )
A.
B.
C.
D.
3.抛物线y=x2-8x+c的顶点在x轴上，则c等于( )
A.-16 B.-4 C.8 D.16
4.若直线y=ax＋b (a≠0）在第二、四象限都无图像，则抛物线y=ax2+bx+c ( )
A.开口向上，对称轴是y轴 B.开口向下，对称轴平行于y轴
C.开口向上，对称轴平行于y轴 D.开口向下，对称轴是y轴
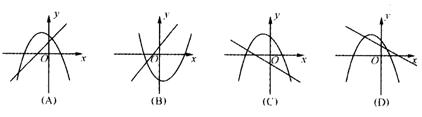
5.一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图像可能是 （ ）
6.已知抛物线y=-x2+mx+n的顶点坐标是（-1，- 3 )，则m和n的值分别是（ ）
A.2,4 B.-2,-4 C.2,-4 D.-2,0
7.对于函数y=-x2+2x-2使得y随x的增大而增大的x的取值范围是 ( )
A.x>-1 B.x≥0 C.x≤0 D.x<-1
8.抛物线y=x2-(m+2)x+3(m-1)与x轴 （ 0
A.一定有两个交点 B．只有一个交点
C．有两个或一个交点 D．没有交点
9.二次函数y=2x2+mx-5的图像与x轴交于点A (x1,
0）、B(x2，0), 且x12+x22=
，则m的值为（ ）
A.3 B.-3 C.3或-3 D.以上都不对
10.对于任何的实数t，抛物线 y=x2 + (2-t) x + t总经过一个固定的点，这个点是 ( )
A . (1, 0) B.（-l, 0) C.（-1, 3) D. (l, 3)
二、填空题（共30 分）
11.抛物线y=-2x+x2＋7的开口向 ，对称轴是 ，顶点是 , 所在象限是 .
12.若二次函数y=mx2-3x+2m-m2的图像过原点，则m的值是 .
13.如果把抛物线y=2x2-1向左平移l个单位，同时向上平移4个单位，那么得到的新的抛物线
是 .
14.对于二次函数y=ax2, 已知当x由1增加到2时，函数值减少4，则常数a的值是 .
15.已知二次函数y=x2-6x+n的最小值为1，那么n的值是 .
16.抛物线在y=x2-2x-3在x轴上截得的线段长度是 .
17.设矩形窗户的周长为6m，则窗户面积S(m2）与窗户宽x (m)之间的函数关系式是 ，自变量x的取值范围是 .
18.设A、B、C三点依次分别是抛物线y=x2-2x-5与y轴的交点以及与x轴的两个交点，则△ABC的面积是 .
19.抛物线上有三点(-2, 3）、（2,-8）、（1,3)，此抛物线的解析式为 .
20.已知一个二次函数与x轴相交于A、B, 与y轴相交于C，使得△ABC为直角三角形，这样的函数有许多，其中一个是 .
三、解答题（共60分）
21.(8分）已知抛物线的顶点坐标为M(l,-2 )，且经过点N(2,3)．求此二次函数的解析式．
22.(10分）把抛物线y=ax2+bx+c向左平移2个单位，同时向下平移l个单位后，恰好与抛物线y=2x2+4x+1重合．请求出a、b、c的值，并画出一个比较准确的示意图．
23.(10分)炮弹的运行轨道若不计空气阻力是一条抛物线．现测得我军炮位A与射击目标B的水平距离为600cm，炮弹运行的最大高度为1200m.
(l）求此抛物线的解析式．
(2）若在A、B之间距离A点500m处有一高350cm的障碍物，计算炮弹能否越过障碍物.
24.(10分）已知函数y = x2+bx-1的图像经过（3,2).
(l）求这个函数的解析式；
(2）画出它的图像，并指出图像的顶点坐标；
(3）当x>0时，求使y
2的x的取值范围．
25.(10分）利用9m长的木料做一“日”字形窗框，它的长和宽各为多少时，窗户面积最大？
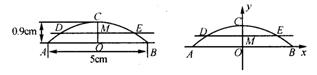26. (12分）卢浦大桥拱形可以近似看作抛物线的一部分．在大桥截面1:11000的比例图上，跨度AB=5cm，拱高OC=0.9cm，线段DE表示大桥拱内桥长，DE//AB ，如左图所示；在比例图上，以直线AB为x轴，抛物线的对称轴为y轴，以1cm作为数轴的单位长度，建立平面直角坐标系，如右图所示．
(1）求出右图x轴以上这一部分抛物线为图像的函数解析式，写出函数定义域；
(2）如果DE与AB的距离OM=0.45cm，求卢浦大桥拱内实际桥长（备用数据：
1.4，计算结果精确到lm).