§3.4二次函数
复习目标
1．二次函数的定义：形如
（a≠0，a，b，c为常数）的函数为二次函数．
2．二次函数的图象及性质：
（1）二次函数的图象是一条抛物线．顶点为（－
，
），对称轴x=－；当a＞0时，抛物线开口向上，图象有最低点，且x＞－，y随x的增大而增大，x＜－，y随x的增大而减小；当a＜0时，抛物线开口向下，图象有最高点，且x＞－，y随x的增大而减小，x＜－，y随x的增大而增大．
（2）当a＞0时，当x=－时，函数有最小值；当a＜0时，当x
=－时，函数有最大值
3．图象的平移：将二次函数y=ax2 (a≠0）的图象进行平移，可得到y=a(x－h)2＋k的图象．
将y=ax2的图象向左（h<0）或向右(h＞0）平移h个单位，再向上(k>0)或向下(k<0)平移k个单位，即可得到y=a(x－h)2 +k的图象，其顶点是（h，k），对称轴是直线x=h，形状、开口方向与抛物线y=ax2相同．
4. 二次函数的图象与系数的关系：
(1) a的符号：a的符号由抛物线的开口方向决定．抛物线开口向上，则a＞0；物线开口向下，则a＜0．
（2）b的符号出的符号由对称轴决定，若对称轴是y轴，则b=0；若对称轴在y轴左侧，则－＜0即＞0，则a、b为同号；若对称轴在y轴右侧，则－＞0，即＜0．则a、b异号．即“左同右异”．
（3）c的符号：c的符号由抛物线与y轴的交点位置确定．若抛物线交y轴于正半轴，则
c＞0，抛物线交y轴于负半轴．则c＜0；若抛物线过原点，则c=0．
（4）△的符号：△的符号由抛物线与x轴的交点个数决定．若抛物线与x轴只有一个交点，则△=0；有两个交点，则△＞0；没有交点，则△＜0 ．
5．二次函数表达式的求法：
⑴若已知抛物线上三点坐标，可利用待定系数法求得；
⑵若已知抛物线的顶点坐标或对称轴方程，则可采用顶点式：
其中顶点为(h，k)对称轴为直线x=h；
⑶若已知抛物线与x轴的交点坐标，则可采用交点式：
,其中与x轴的交点坐标为（x1，0），（x2，0）
6．二次函数与一元二次方程的关系：
（1）一元二次方程
就是二次函数当函数y的值为0时的情况．
（2）二次函数的图象与x轴的交点有三种情况：有两个交点、有一个交点、没有交点；当二次函数的图象与x轴有交点时，交点的横坐标就是当y=0时自变量x的值，即一元二次方程ax2＋bx＋c=0的根．
（3）当二次函数的图象与
x轴有两个交点时，则一元二次方程有两个不相等的实数根；当二次函数的图象与x轴有一个交点时，则一元二次方程ax2＋bx＋c＝0有两个相等的实数根；当二次函数y＝ax2+ bx+c的图象与 x轴没有交点时，则一元二次方程没有实数根．
典例精析
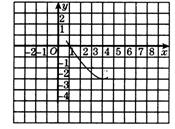
【例1】(1) 已知抛物线
的部分图象如图，则
再次与x轴相交时的坐标是（ ）
A．（5，0） B。（6，0）
C．（7，0） D。（8，0）
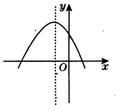
（2）已知二次函数的图象如图所示，则a、b、c满足（ ）
A．a＜0，b＜0，c＞0 B．a＜0，b＜0，c＜0
C．a＜0，b＞0，c＞0 D．a＞0，b＜0，c＞0
【分析】（1）由
，可知其对称轴为x=4,而图象与x轴已交于(1，0)，则与x轴的另一交点为(7，0)。
（2）由抛物线开口向下可知a＜0；与y轴交于正半轴可知c＞0；抛物线的对称轴在y轴左侧，可知－ ＜0．则b＜0．故选A．
【解答】（1）C （2）A
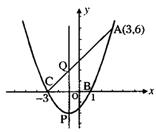【例2】（2006宁波）如图，抛物线与x轴相交于B（1，0）、C（-3，0），且过点A（3，6）。
（1） 求a，b，c的值。
（2） 设抛物线的顶点为P，对称轴与线段AC相交于点Q，连结CP、PB、BQ。试求四边形PBQC的面积。
【分析】本题第（1）小题考察用待定系数法求抛物线的解析式，结合条件可以考虑用交点式。第（2）小题关键是求出Q点的坐标，因为它是对称轴与线段AC的交点，所以要先求出直线AC的解析式。
【解答】（1）由题意可设：
，
把点A（3，6）坐标代入可得 
所以
， 即
所以
（2）
顶点P的坐标为（-1，-2），对称轴是直线
而直线AC的解析式为
所以对称轴与线段AC的交点Q的坐标为（-1，2）
设对称轴与x轴相交于点D，则可得：DP=DB=DQ=DC=2
所以四边形PBQC的面积为8。
【例3】已知
，
≠0，把抛物线
向下平移1个单位，再向左平移5个单位所得到的新抛物线的顶点是（－2，0），求原抛物线的解析式。
【分析】①由可知：原抛物线的图像经过点（1，0）；②新抛物线向右平移5个单位，再向上平移1个单位即得原抛物线。
【解答】可设新抛物线的解析式为
，则原抛物线的解析式为
，又易知原抛物线过点（1，0）
∴
，解得
∴原抛物线的解析式为：
【例4】如图是抛物线型的拱桥，已知水位在AB位置时，水面宽
米，水位上升3米就达到警戒水位线CD，这时水面宽
米，若洪水到来时，水位以每小时0.25米的速度上升，求水过警戒线后几小时淹到拱桥顶？
【分析】本题关键是建立合适的直角坐标系。
【解答】以AB所在直线为
轴，AB的中点为原点，建立直角坐标系，则抛物线的顶点M在
轴上，且A（
，0），B（
，0），C（
，3），D（
，3），设抛物线的解析式为
，代入D点得
，顶点M（0，6），所以
（小时）
【例5】已抛物线
（
为实数）。
（1）为何值时，抛物线与轴有两个交点？
（2）如果抛物线与轴相交于A、B两点，与轴交于点C，且△ABC的面积为2，求该抛物线的解析式。
【分析】抛物线与轴有两个交点，则对应的一元二次方程有两个不相等的实数根，将问题转化为求一元二次方程有两个不相等的实数根应满足的条件。
【解答】（1）由已知有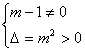
，解得
且
（2）由
得C（0，－1）
又∵
∴
∴
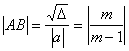
或
∴
或
课内巩固
1. （2006临安）抛物线y=3(x-1)
+1的顶点坐标是（ ）
A．（1，1） B．（-1，1） C．（-1，-1） D．（1，-1）
2．已知直线y=x与二次函数y=ax2 －2x－1的图象的一个交点 M的横标为1，则a的值为（ ）
A、2 B、1 C、3 D、 4
3．二次函数
的图像向右平移3个单位，再向下平移2个单位，得到函数图像的解析式为
，则
与
分别等于（ ）
A、6、4 B、－8、14
C、4、6 D、－8、－14
4．（2006湖州）已知二次函数y=x2－bx+1（－1≤b≤1），当b从－1逐渐变化到1的过程中，它所对应的抛物线位置也随之变动。下列关于抛物线的移动方向的描述中，正确的是（ ）
A、先往左上方移动，再往左下方移动;
B、先往左下方移动，再往左上方移动;
C、先往右上方移动，再往右下方移动;
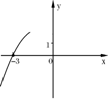D、先往右下方移动，再往右上方移动
5．（2006诸暨）抛物线y=ax2+2ax+a2+2的一部分如图所示，那么该抛
物线在y轴右侧与x轴交点的坐标是 ( )
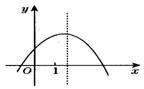A．（，0）； B．（1， 0）；
C．（2， 0）； D．（3， 0）
6．已知函数
的图象如图所示，给出下列关于系数a、b、c的不等式：①a＜0，②b＜0，③c＞0，④2a＋b ＜0，⑤a＋b＋c＞0．其中正确的不等式的序号为___________。
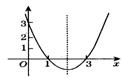7．已知二次函数的图象如图所示：
（1）这个二次函数的解析式是y=__________．
（2）当x=_______时，y=3；
（3）根据图象回答：当x______时，y＞0．
8．某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程。下面的二次函数图象（部分）刻画了该公司年初以来累积利润S（万元）与销售时间
（月）之间的关系（即前个月的利润总和S与之间的关系）。根据图象提供的信息，解答下列问题：
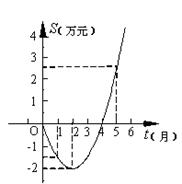（1）由已知图象上的三点坐标，求累积利润S（万元）与时间（月）之间的函数关系式；
（2）求截止到几月末公司累积利润可达到30万元；
（3）求第8个月公司所获利润是多少万元？
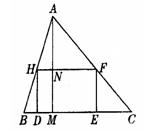
9．四边形DEFH为△ABC的内接矩形，AM为BC边上的高且长为8厘米，BC长为12厘米，DE长为x，矩形的面积为y，请写出y与x之间的函数关系式，并判断它是不是关于x的二次函数.
课外拓展
A组
1. （2006舟山）二次函数y=x2+10x-5的最小值为（ ）．
A．-35 B．-30 C．-5 D．20
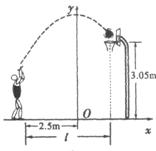
2. （2006绍兴）小敏在某次投篮中，球的运动路线是抛物线y=
的一部分(如图)，若命中篮圈中心，则他与篮底的距离
是( )
A．3.5m B．4m C．4.5m D．4.6m
3. 函数y= x2－4的图象与y 轴的交点坐标是（ ）
A.（2，0） B.（－2，0） C.（0，4）D.（0，－4）
4.（2006苏州）抛物线y＝2x2+4x+5的对称轴是x=_________ ．
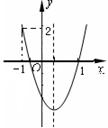5.（2006浙江）如图，二次函数
的图象开口向上,图像经过点（-1，2）和（1，0）且与y轴交于负半轴．
（1）给出四个结论：①＞0；②
＞0；③＞0； ④a+b+c=0 其中正确的结论的序号是
．
（２）给出四个结论：①abc＜0；②2a+＞0；③a+c=1；
④a＞1．其中正确的结论的序号是
。
6. 已知二次函数的图象开口向下，且与y轴的正半轴相交，请你写出一个满足条件的二次函数解析式：_______________.
7. 若抛物线
的最低点在轴上，则的值为 。
8.已知抛物线
过三点（－1，－1）、（0，－2）、（1，l）．
（1）求这条抛物线所对应的二次函数的表达式；
（2）写出它的开口方向、对称轴和顶点坐标；
（3）这个函数有最大值还是最小值？ 这个值是多少？
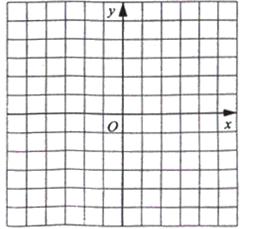9．(2006盐城)已知：抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧)，顶点为P．
(1)求A、B、P三点坐标；
(2) 在如图的直角坐标系内画出此抛物线的简图，并根据简图写出当x取何值时，函数值y大于零；
(3)确定此抛物线与直线y=-2x+6公共点的个数，并说明理由.
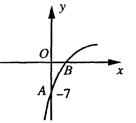10.（2005枣庄）已知抛物线
的图象的一部分如图所示，抛物线的顶点在第一象限，且经过点A(0，-7)和点B.
(1)求a的取值范围；
(2)若OA=2OB，求抛物线的解析式．
B组
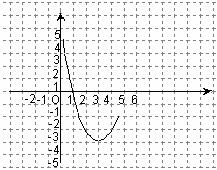
11．（2005常州）已知抛物线
的部分图象如图,则抛物线的对称轴为直线x= ,满足y＜0时的x的取值范围是 ,将抛物线
向 平移 个单位,则得到抛物线
.
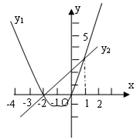12．（2006大连）如图是二次函数y1＝ax2＋bx＋c和一次函数y2＝mx＋n的图象，观察图象写出y2≥y1时，x的取值范围______________。
13．阅读材料：当抛物线的解析式中含有字母系数时，随着系数中的字母取值的不同，抛物线的顶点坐标也将发生变化．
例如：由抛物线
①，有y=
②，所以抛物线的顶点坐标为（m，2m－1），即
当m的值变化时，x、y的值随之变化，因而y值也随x值的变化而变化，将③代人④，得y=2x—1⑤．可见，不论m取任何实数，抛物线顶点的纵坐标y和横坐标x都满足关系式y=2x－1。回答问题：（1）在上述过程中，由①到②所用的数学方法是________，其中运用了_________公式，由③④得到⑤所用的数学方法是______；（2）根据阅读材料提供的方法，确定抛物线
顶点的纵坐标与横坐标x之间的关系式_________.
14．（2006台州）如图，已知抛物线y=ax2+4ax+t（a＞0）交x轴于A、B两点，交y轴于点C，点B的坐标为（－1，0）.
（1）求此抛物线的对称轴及点A的坐标；
（2）过点C作x轴的平行线交抛物线的对称轴于点P，你能判断四边形ABCP是什么四边形吗？请证明你的结论；
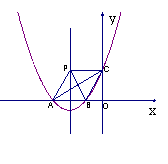（3）连结AC，BP，若AC⊥BP，试求此抛物线的解析式.
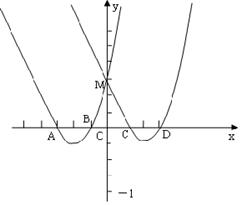15．（2006大连）如图，抛物线E：y＝x2＋4x＋3交x轴于A、B两点，交y轴于M点，抛物线E关于y轴对称的抛物线F交x轴于C、D两点。
（1）求F的解析式；
（2）在x轴上方的抛物线F或E上是否存在一点N，使以A、C、N、M为顶点的四边形是平行四边形。若存在，求点N的坐标；若不存在，请说明理由；
（3）若将抛物线E的解析式改为y＝ax2＋bx＋c ，试探索问题（2）。
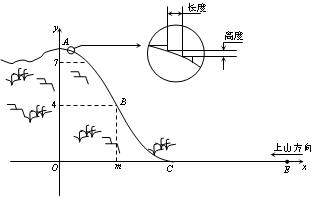16．（2006嘉兴）某旅游胜地欲开发一座景观山．从山的侧面进行堪测，迎面山坡线ABC由同一平面内的两段抛物线组成，其中AB所在的抛物线以A为顶点、开口向下，BC所在的抛物线以C为顶点、开口向上．以过山脚（点C）的水平线为x轴、过山顶（点A）的铅垂线为y轴建立平面直角坐标系如图（单位：百米）．已知AB所在抛物线的解析式为y＝－
x2＋8，BC所在抛物线的解析式为y＝(x－8)2，且已知B（m，4）．
（1）设P（x，y）是山坡线AB上任意一点，用y表示x，并求点B的坐标；
（2）从山顶开始、沿迎面山坡往山下铺设观景台阶．这种台阶每级的高度为20厘米，长度因坡度的大小而定，但不得小于20厘米，每级台阶的两端点在坡面上（见图）．
①分别求出前三级台阶的长度（精确到厘米）；
②这种台阶不能一起铺到山脚，为什么？
（3）在山坡上的700米高度（点D）处恰好有一小块平地，可以用来建造索道站．索道站的起点选择在山脚水平线上的点E处，OE＝1600（米）．假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线，解析式为y＝
(x－16)2．试求索道的最大悬空高度．
反思纠错
1． 
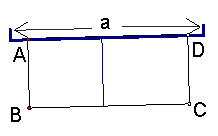如图，有长为24米的篱笆，一面利用墙（墙的最大可利用长度a为10米）围成中间隔一道篱笆的长方形花圃。设花圃的宽AB为米，面积为
平方米。
（1） 求与的函数关系式；
（2） 如果要围成面积为45平方米的花圃，AB的长是多少米？
（3） 能围成面积比45平方米更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由。
解：（1）花圃宽米，长为
米，则它的面积与的函数关系式为
。
（2） 当
时，
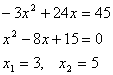
所以 ， 当AB长为3米或5米时花圃的面积为45平方米。
（3）
所以，能围成面积比45平方米更大的花圃，它的最大面积为48平方米。
上述解法正确吗？为什么？