1． 九年级数学自测试题
2． 某件商品按原价出售可获利x%，现因进价降低10%，按原定价出售则可获利（x+15）%，则x=___________。
3． 我国股市交易中，每买卖一次需复交交易款的千分之七点五作为交易费用，某投资者以每股10元的价格习入上海某股票1000股，当该股票涨到12元时全部卖出，该投资者实际盈利为____________元。
3．某商场根据市场销售变化，将A商品连续两次提价20%，同时将B商品连续两次降价20%，结果都以每件23.04元出售，此时商场若同时售出A、B两商品各一件的盈亏情况为（ ）
A 不亏不盈 B 盈6.12元 C 亏6.02 D 亏5.92
4．某品牌彩电为了打开市场，促进销售，准备对其特定型号彩电降价，有四种方案供选择：①先降价12%，再降价8%②先降价8%，再降价12%③先降价10%，再降价10%④一次性降价20%。在这四种方案中，降价幅度最小的是____________。
5．商业毛利是指售出价减去买入价的差，某种商品降价前每件毛利是售出价的15%，每天售出100件，降价（买入价不变）后每天比原来多销售150件且降价后每天毛利总额是降价前每天毛利总额的
，则售价降低了（ ）
A 5% B 8% C 10% D 12%
6．某公司向银行贷款40万元，用来开发某种新产品，已知该贷款年利率15%（不计复利），每个新产品成本为2.3万元，售价4元，应纳税款为销售额的10%，如果每年生产该产品20万个，并把所得利润用来归还贷款，则还清贷款所需年数为（ ）
A 1.5年 B 2年 C 2.5年 D 3年
7．1999年11月1日起，全国储蓄存款征收利息税，税率为20%，即利息所得的20%，由储蓄点代扣代征，某人在1999年11月存入人民币1.6万元，年利率为2.25%，一年后可得本息和（扣税后）_______元。
8． 工业废气年排放量为450万立方米，为了改善某市的大气环境质量，决定分两期投入治理，使废气的年排放量减少到288万立方米，如果每期治理中废气减少的百分率相同。（1）求每期减少的百分率是多少？（2）预计第一期治理中每减少1万立方米废气需投入3万元，第二期每减少1万立方米需投入4.5万元，问完成两期治理后共需投入多少万元？
9． 某工程由甲、乙两队合做6天完成，厂家需付甲乙两队共8700元，乙丙两队合做10天完成，厂家需付乙丙两队共9500元，甲丙两队合做5天完成全部工程的
，厂家需付甲丙两队共5500元。（1）求甲乙丙各队单独完成全部工程各需多少天？（2）该工程要求不超过15天完成全部工程。问可由哪能队单独完成此项工程？
10． 工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料生产A、B两种产品共50件，已知生产1 件A种产品需甲种原料9千克，乙种原料3千克，可获利润700元，生产1 件B种产品需用甲种原料4千克，乙种原料10千克，可获利润1200元。
a) 按要求安排A、B两种产品的生产件数，有哪几种方案，请你设计出来。
b) 设生产A、B两种产品获总利润为Y元，其中一种产品的生产件数为x件，试写出用含x的代数式表示Y的式子，并说明哪能一种方案利润最大？最大利润是多少元？
11． 场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当降价的措施，经调查发现，如果每件衬衫降价一元，商场平均每天可多售出2件。
a) 若商场平均每天要盈利1200元，每件衬衫应降价多少元？
b) 设商场平均每天盈利为Y，则每件衬衫降价多少元时，商场获利最大？最大值是多少？
12．某车间有20名工人，每天可加工甲种零件5个或乙种零件4个。在这20名工人中，派x人加工甲种零件，其余的加工乙种零件，已知每加工一个甲种零件可获利16元，每加工一个乙种零件可获利24元。
c) 出此车间每天所获利润Y（元）与x（人）之间的关系（用含x的代数式表示Y）
d) 若要使车间获利不低于1800元，问至少要派多少人加工乙种零件？
13．某农场开挖一条长700米的渠道，开工后每天比原计划多挖20米，结果提前4天完成任务，原计划每天挖多少米？
14．甲乙两人分别从相距27千米的A、B两地同时出发，相向而行，3小时后两人相遇，相遇后各以原来的速度继续前进，甲到达B地比乙到达A地早1小时21分。求甲、乙两人的速度。
15．某拖拉机厂，今年元月份生产出一批甲、乙两种新型拖拉机，其中乙型16台，从二月份起，甲型每月增产10台，乙型每月按相同的增长率逐月递增，又知二月份甲、乙两种的产量之比是3：2，三月份甲、乙两种产量之和为65台，求乙型拖拉机每月的增长率。
16．甲乙两人均以每小时60千米的速度先后驾车从A地到B地去办事，8点20分时，甲离A地的距离是乙离A地距离的2倍，行至8点26分时，甲离A地与乙离A地的距离比为2：3，求甲出发的时间。
17．先阅读下面一段文字，然后解答问题。
某运输部门规定：办理托运，当一件物品的重量不超过a千克（a<18）时，需付基础费30元和保险费b元，为限制过重物品的托运，当一件物品的重量超过千克时，除了付以上基础费和保险费外，超过部分每千克还需付c元超重费。
设某件物品的重量为x千克，支付费用为y元。
（1）
当
时，y=___________（用含b的代数式表示）
当
时，y=_______________（用含x和
,b,c的代数式表示）
| 物品重量 （千克） | 支付费用（千克） |
| 12 | 33 |
| 18 | 39 |
| 25 | 60 |
（2）甲，乙，丙三人各托运了一件物品。
物品重量与支付费用如右表所示；
① 试根据以上提供的信息确定,b,c的值，并写出支付费用y（元）与每件物品重量x（千克）的关系式（用x的代数式表示y）
② 试问在物品可拆分的情况下，用不超过120元的费用能否托运50千克物品？若能，请设计出其中一种方案，并求出托运费用；若不能，请说明理由。
18．为了加快教学手段的现代化，某校计划购置一批电脑，已知甲公司的报价是每台5800元，优惠条件是购买10台以上则超过10台的部分按报价的70%计算，乙公司的报价也是每台5800元，其优惠条件是为了支持教育每台按报价的85%计算，假如你是学校的负责人，在电脑的品牌、质量和售后服务等完全相同的前提下，你将如何选择？请说明理由。
19．经测算，某林场现有生长着木材存量为a立方米，已知木材生长的年增长率为25%，为满足生产、生活需要，该林场每年采伐加工x立方米木材。
（1） 用含a与x的代数式表示一年后该林场的木材存量为_____________。
（2） 用含a与x的代数式表示二年后该林场的木材存量为_____________。
（3） 若条件中的a=122万，要保证三年后该林场木材存量达到1.5a立方米，问该林场每年采伐加工的木材最多是多少立方米
20．某校学生到离校12千米的工厂参观，一部分学生骑着自行车先走，骑了一半路程时，其余学生才乘汽车从学校出发，当骑车的学生闻目的地还有4.5千米时，汽车刚好行了一半路程，结果汽车比自行车早20分钟到达工厂，求自行车和汽车的速度。
21．某旅社有100张床位，每床每晚收费10元时客床可全部租出，若每床每晚收费提高2，元，则减少10张床位租出，若每晚收费再提高2元，则再减少10张床位租出，以每次提高2元的这种方法变化下去，为了投资少而利润大，每床每晚应提高（ ）
A 4元或6元 B 4元 C 6元 D 8元
22．如图示，甲乙两人分别从正方形广场ABCD的顶点B、C两点出发，甲由C点向D点运动，速度为2千米/秒，乙由B点向C点运动，速度为1千米/秒。若正方形广场的周长为40千米，问几分钟后，甲乙两人所在的位置与点C构成一个含
的直角三角形？
23．为了参加北京市申办2008年奥运会的活动。]
（1） 某班学生争取到制作249面矩形彩旗的任务，有10名学生因故未能参加制作，因此这班的其余学生人均要比原计划多做4面旗才能完成任务。问这个班有多少名学生？
（2） 如果有长为1，a(a>1)的一块绸布，要将其裁出三面矩形彩旗（面料没有剩余）且使每面彩旗长和宽之比与原绸布的长与宽之比相同。画出两种不同的裁剪方法示意图，并写出相应a的值。（不写计算过程）
24．商场出售的A型冰箱每台2190元，日耗电量为1度，而B型冰箱每台售价比A型冰箱高出10%，日耗电量为0.55度。现将A型冰箱打折出售，问商场至少打几折，消费者购买才合算？（按使用期为10年，每年365天，每度电按0.40元计算）
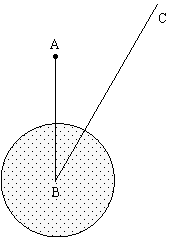25．台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力．据气象观测，距沿海某城市A的正南方向220千米B处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级．该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动，且台风中心风力不变．若城市所受风力达到或超过四级，则称为受台风影响．
（1）该城市是否会受到这次台风的影响？请说明理由．
（2）若会受到台风影响，那么台风影响该城市的持续时间有多长？
（3）该城市受到台风影响的最大风力为几级？
26．甲，乙两人分别从相距27公里的A、B两地同时出发相向而行，3小时相遇，相遇后两人各以原来的速度继续前进，甲到达B地比乙到达A地早1小时21分，求两人的速度各是多少？
27．某车间加工360个零件，加工2天后，改进操作方法，每天多加工20个零件，结果提前4天完成，问改进操作方法前，每天加多少个零件？
28．一商店将进货价每个10元的商品按每个18元出售时，每天可卖出60个，商店经理到市场上做了一番调查后发现，若将这种商品的售价（在每个18元的基础上）每降价1元，则日销售量就增加10个，当获得每日最大利润时，此商品售价应定为多少元？