第四章相似三角形测试卷
（时间90分钟，总分150分）
班级 学号 姓名 得分
一、选择题（每题4分，共48分）
1、下列多边形一定相似的为（ ）
A、两个矩形 B、两个菱形 C、两个正方形 D、两个平行四边形
2、下列说法不正确的是（ ）
A、 两对应角相等的三角形是相似三角形；
B、两对应边成比例的三角形是相似三角形；
C、三边对应成比例的三角形是相似三角形；
D、以上有两个说法是正确。
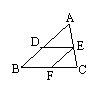
3、如图，DE∥BC，EF∥AB，则图中相似三角形有（ ）
A、2对 B、3对 C、4对 D、5对
4、已知3x=4y，则
= （ ）
A、
B、
C、
D、以上都不对
5、下列各组中得四条线段成比列得是（ ）
A、4cm、2cm、1cm、3cm B、1cm、2cm、3cm、4cm
C、25cm、35cm、45cm、55cm D、1cm、2cm、20cm、40cm
6、若x是3和6的比例中项，则x的值为 （ ）
A、
B、
C、
D、
7、若P是线段AB的黄金分割点（PA＞PB），设AB=1，则PA的长约为 （ ）
A、0.191 B、0.382 C、0.5 D、0.618
8、如果
，则下列正确得是（ ）
A、
B、
C、
D、
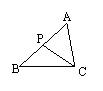9、如图，若P为△ABC的边AB上一点（AB>AC），则下列条件不一定能保证△ACP∽△ABC的有（ ）
A、∠ACP=∠B B、∠APC=∠ACB C、
D、
10、已知D、E为△ABC的边AB、AC上的两点，且AB=8，AC=6，AD=4，AE=3，则
∶
=（ ）
A、1∶2 B、1∶4 C、1∶3 D、2∶5
11、下列3个图形中是位似图形的有（ ）
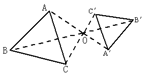
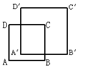
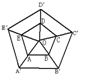
A、0个 B、1个 C、2个 D、3个
12٭、已知，如图（上右）△ABC是锐角三角形，正方形DEFG的一边在BC上，其余两个定点分别在AB、AC上，记△ABC的面积为
，正方形DEFG的面积为
，则有 （ ）
A、
B、
C、
D
二、填空题（每题4分，共32分）
13、在比例尺为1：的“中国政区”地图上，量得甲市与乙市之间的距离是6.5cm，则这两市之间的实际距离为 km；
14、小明的身高是1.6m，他的影长为2m，同一时刻教学楼的影长为24m，则教学楼的高是
；
15、已知AD为Rt△ABC斜边BC上的高，且AB=15cm，BD=9cm，则AD=
，CD=
。
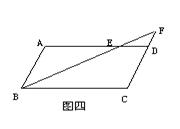
16、如图四，在平行四边形ABCD中，AB = 4cm ,AD = 7cm , ∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF = _________cm
17、若△ABC∽△A′B′C′，且
，△ABC的周长为12cm，则△A′B′C′的周长为
；
18、已知：x∶y∶z=2∶3∶4，则
的值为 。
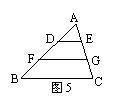
19、٭如图5,ΔABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,
则
=
20、以坐标原点O为位似中心，作的位似图形，并把的边长放大5倍. 如果四边形ABCD的坐标A（2，3），B（4，0），C（6，0），D（5，5）那么它们的对应点的坐标是
。（只要一种）
三、解答题（6+8+8+8+8+8+8+10+14=70分）
21、（6分）请作出五边形ABCDE以点O为位似中心的位似图形，使得像和原图形的位似比是1：2。
22、已知AB∥CD，AD、BC交于点O。（8分）
（1）、试说明△AOB∽△DOC。
（2）、若AO＝2，DO＝3，CD＝5，求AB的长。
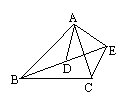23、如图，已知
，试说明∠BAD=∠CAE。（8分）
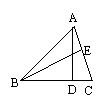
24、如图，已知AD、BE是△ABC的两条高，试说明AD·BC=BE·AC（8分）
 |
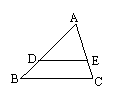25、已知，如图， 在△ABC中，DE∥BC，AD=5，BD=3，求S△ADE：S△ABC的值。（8分）
26、有一块三角形的土地，它的底边BC＝100米，高AH＝80米。某单位要沿着地边BC修一座底面是矩形DEFG的大楼，D、G分别在边AB、AC上。若大楼的宽是40米（即DE＝40米），求这个矩形的面积。（8分）
 |
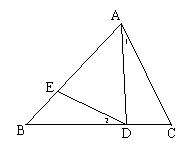
27、（10分）已知:如图,ΔABC中,AD=DB,∠1=∠2.求证:ΔABC∽ΔEAD.
28、（14分）如图，已知过A（2，4）分别作x轴、y轴的垂线，垂足分别为M、N，若点P从O点出发，沿OM作匀速运动，1分钟可到达M点，点Q从M点出发，沿MA作匀速运动，1分钟可到达A点。
（1）经过多少时间，线段PQ的长度为2？
（2）写出线段PQ长度的平方y与时间t之间的函数关系式和t的取值范围；
（3）٭在P、Q运动过程中，是否可能出现PQ⊥MN？若有可能，求出此时间t；若不可能，请说明理由；
（4）٭是否存在时间t，使P、Q、M构成的三角形与△MON相似？若存在，求出此时间t；若不可能，请说明理由；
y
N A
Q
 |
O P M x