九年级数学(上)第一次月考质量调研试题()
本卷总分120分,考试时间90分钟
一、选择题(每小题3分,共36分)
1.下列各项是一元二次方程的是 ( )
A.![]() B.
B.![]()
C. ![]() D.
D. ![]() -1
-1
2.下列计算正确的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.用配方法将二次三项式![]() 变形,结果为
( )
变形,结果为
( )
A.(x -![]() )
)![]() B. 2(x-
B. 2(x-![]() )
)![]()
C.2(x-![]() )
)![]() =0
D.(x-
=0
D.(x-![]() )
)![]() =0
=0
4.有一对角线互相垂直的四边形,对角线长分别为(6![]() +1)与(6
+1)与(6![]() -1),则该四边形的面积为
( )
-1),则该四边形的面积为
( )
A. 179 B.
![]() C.
89.5
D.不能确定
C.
89.5
D.不能确定
5.若方程mx2+3x-4=3x2是关于x的一元二次方程,则m的取值范围是 ( )
A.m≠3 B m ≠1 C m≠0 D m≠2
6.某校毕业生升入重点中学人数由05年的200人上升到07年的242人(公费),平均每年增长 ( )
A.8.5% B.9% C.9.5% D.10%
7.化简二次根式![]() 的结果是
( )
的结果是
( )
A.-a![]() B.
B.![]() C.
C.![]() D.
D. ![]()
8.如果等式(x+1)0=1和![]() =2-3x同时成立,那么需要的条件是 ( )
=2-3x同时成立,那么需要的条件是 ( )
A.x≠-1 B.x<![]() 且x≠-1 C.x≤
且x≠-1 C.x≤![]() 或x≠-1 D.x≤
或x≠-1 D.x≤![]() 且x≠-1
且x≠-1
9.关于![]() 的方程
的方程![]() 的一个根是0,则
的一个根是0,则![]() 的值为
( )
的值为
( )
A. 1 B. -1或1 C.-1 D. 0.5
10.在一幅长100cm,宽80cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形图.如果要使整个挂图的面积是100![]() ,设金色纸边的宽为xcm,那么x满足的方程是( )
,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+180x-1000=0 B.x2+90x-500=0 C.x2-180x-1000=0 D.x2-90x-500=0
11.若关于x的方程x2 – x(k-x)+3=0无实根,则k可取的最小整数为 ( )
A.-5 B.-4 C.- 3 D.- 2
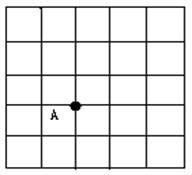
12.如图,点A是5×5网格图形中的一个格点(小正方形的顶点),图中每个小正方形的边长为1,以A为其中的一个顶点,面积等于2.5的格点等腰直角三角形(三角形的三个顶点都是格点)的个数是 ( )
A.10 B.12 C.14 D.16
二、填空题(每小题4分,共24分)
13.若最简二次根式![]() 与
与![]() 可以合并,则a= b=
可以合并,则a= b=
14.请写出一个解分别为![]() =0,
=0,![]() =2的一元二次方程
=2的一元二次方程
15.生物兴趣小组的同学,将自己收集的标本向其他同学各赠送2件,全组共互赠了420件,如果全组有x名同学,则可得方程为 。(不解方程)
16.一元二次方程的一般式为 若4a-2b+c=0,则方程必有一个根为
17.若![]() 与
与![]() 互为相反数,则以
互为相反数,则以![]() 为边长的直角三角形的第三边长为
为边长的直角三角形的第三边长为
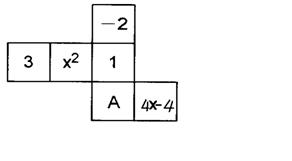
18.如图(13题上方)是一个正方体的展开图,标注了字母![]() 的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,且标注的数字相同的不超过2个,则A的取值范围是______.
的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,且标注的数字相同的不超过2个,则A的取值范围是______.
三、解答题(共60分)
19.(20分)(1)计算: ![]() (2)解方程
(2)解方程![]()
(3)x2-3x+2=-2
(4)已知:X=![]() ,求代数式X2+4X+13的值
,求代数式X2+4X+13的值
20.(6分)阅读下面的例题:解方程![]()
解:①当x≥0时, ②当x<0时,
原方程化为x2 – x –2=0, 原方程化为x2 + x –2=0,
解得 x1=2 x2= - 1(舍去) 解得 x1=1(舍去)x2= -2
∴原方程的根是x1=2 x2= - 2
请参照例题解方程![]()
23.(6分)是否存在这样的非负整数m,使得关于x的一元二次方程![]() 有两个实数根?若存在,请求出m的值,并求解此方程;若不存在,请说明理由。
有两个实数根?若存在,请求出m的值,并求解此方程;若不存在,请说明理由。
21.(8分)将一块长18米,宽15米的矩形荒地修建成一个花园(阴影部分为路),所占的面积为原来荒地面积的三分之二. (精确到0.1米)
(1)设计方案1(如图①)花园中修两条互相垂直且宽度相等的小路;
(2)设计方案2(如图②)花园中每个角的扇形都相同。
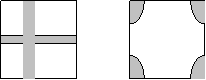 上述两种方案是否都能符合条件?若能,请计算出图①中小路的宽和图②中扇形的半径;若不能符合条件,请说明理由。
上述两种方案是否都能符合条件?若能,请计算出图①中小路的宽和图②中扇形的半径;若不能符合条件,请说明理由。
|
|
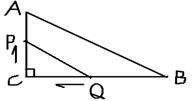
22.(6分)如图,在Rt△ABC中,点P由C点出发以1cm/s向A匀速运动,同时点Q从B点出发以2cm/s向C点匀速移动,已知AC=4cm,BC=12cm,
⑴若记点的移动时间为t,试用含有 t的代数式表示Rt△PCQ与四边形PQBA的面积。.
⑵当P、Q处在什么位置时,四边形PQBA的面积最小,并求最小值。
24.(7分)已知长方形的长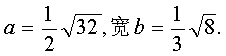
(1)求长方形的周长;
(2)求与长方形等面积的正方形的周长,并比较它与长方形周长的大小关系。
(3)在面积相等的正方形与长方形中,周长较小的是
试证明你的结论。
25.(7分)台州高速三门段某处一交警10:05接到上司命令,要求他马上到前方12km处拦截一冲卡的犯罪嫌疑人(最大速度匀速逃跑),此时警车速度指针为30千米/小时,里程表示数为4357千米,他马上开足马力,几分钟后速度指针为120千米/小时(最大车速,此后保持匀速),里程表示数为4362千米,若这段时间汽车的速度是匀速增加的,请问:
(1) 警车匀加速用了几分钟?警车速度每分钟增加多少千米/小时?
(2) 里程表显示4360km时,是几点几分?(精确到分)
(3) 若要求他在半小时内追上嫌疑人,则嫌疑人的最大车速为多少?
九年级(上)第一次月考质量调研试题(数学)
(答案)仅供参考
一、选择题
D C BCA DCDBB BD
二、填空
13.a=-10 b=-18
14.不唯一,x(x-2)=0
15.X(x—1)=210
16.![]() x= -2
x= -2
17.![]() 或 10
或 10
18.A≠4
三、解答
(1)![]() (2)x1 =-3 x2 =3
(2)x1 =-3 x2 =3
(3)无实数解 (4)14
20.X=1 或 x=-2
21.X2 =3 r=5.4
22.S=- t2 +6t
S= t2-6t+24
S=(t-3)2+15
t = 3 时,四边形最小
即PC =3cm QC=12-2t
=6cm
四边形PQBA的面积。.
23.
m= 1
x=![]()
24.10元/盏
25.
(1)15分钟 ; 22。5km/h
(2)10:08
(3) 90km/h