九年级数学第二次月考试卷
考生注意：
1．数学试卷分试题卷和答题卷，答完题后只交答题卷，试题卷自己保留 2.本试卷满分 120 分，考试时间 100 分钟。3.．请您仔细思考、认真答题，不要过于紧张，再次提高你学习数学的兴趣和自信心，你的成功，就是送给老师和父母的最好的礼物！祝考试顺利！
一、精心选一选（本题共10 小题，每小题4分，满分40分）
每一个小题都给出代号为A、B、C、D的四个结论，其中只有一个是正确的，把正确结论的代号写在题后的括号。每一小题：选对得 3 分，不选、选错或选出的代号超过一个的（不论是否写在括号内）一律得0分。
1、若
，则
的值是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
2、若
，且它们的面积比为
，则周长比是（ ）
Ａ．
Ｂ．
Ｃ． Ｄ．
3、在
地图上，
两点之间的距离是
，则两地的实际距离是（ ）
Ａ．
千米 Ｂ．
千米 Ｃ．
千米 Ｄ．
千米
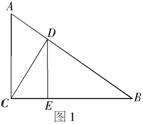4、如图1，在
中，
是斜边上的高，
，
垂足为
，则图中与
相似的三角形（不包括）
共有（ ）
Ａ．5个 Ｂ．4个 Ｃ．3个 Ｄ．2个
5、如图，点
把线段
分成两条线段
和
，如果
，
那么称线段被点黄金分割，与的比叫做黄金比，其比值是（ ）
A．
B．
C．
D．
6、李红同学遇到了这样一道题：
tan(α+20°)=1，你猜想锐角α的度数应是（ ）
A.40° B.30° C.20° D.10°
7、在△ABC中，若tanA=1，sinB=
，你认为最确切的判断是（ ）
A.△ABC是等腰三角形 B.△ABC是等腰直角三角形
C.△ABC是直角三角形 D.△ABC是一般锐角三角形
8、如图2，已知△ABC，则下列4个三角形中，与△ABC相似的是（ ）
A
 | |||
 | |||
6 6 5
5 5
5
5 400 5
750 750 300
B C 5 5 5
8题 A B C D
9、．在Rt△ABC中，∠C=90°，当已知∠A和a时，求c，应选择的关系式是（ ）
A．c=
B．c=
C．c=a·tanA D．c=a·cosA
10、．下列说法中，正确的是（ ）
A、两个多边形相似，则它们一定是位似图形
B、两个位似图形的位似中心可能不止一个
C、位似图形一定是相似图形
D、两个多边形相似，面积比一定是相似比
二、细心填一填（填空题（本题共 6 小题，每小题 3 分，满分 18 分）
11、．若线段
成比例，其中
，则
．
12、在Rt△ABC中，∠C＝90°，若AC＝3，AB＝5，则cosB的值为__________。
13、在Rt△ABC中，∠C=90°.若sinA=
，则sinB=
14、设==，则=______，=______
15、如图，要使DAED和DABC相似，已具备条件__________________，还需补充的条件是_________，或_________，或_________。
16、如图，为平行四边形
的边延长线上一点，连结
，交边于点
．在不添加辅助线的情况下，请写出图中一对相似三角形：
．
16题
答题卷
初三数学（满分120分沪科版）
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||
| (1～10) | (11～16) | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | ||
| 得 分 | |||||||||||
| 得 分 | 评卷人 |
一、选择题：（每题4分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
| 得 分 | 评卷人 |
二、填空题（每小题3分，共18分）
11、 12、
13、 14、
15、 16、
三、解答题（共62分）
| 得 分 | 评卷人 |
17、（（本小题8分）计算和解直角三角形：
(1)cos30°+
sin45° (2)6tan2
30°－sin 60°－2sin 45°
（3）根据下列条件，求出Rt△ABC(∠C=90°)中未知的边和锐角.
①BC=8，∠B=60°.
②AC=
，AB=2.
| 得 分 | 评卷人 |
18（本小题8分）如图4，是等边三角形，
在所在的直线上，且AB
AC=BDCE．
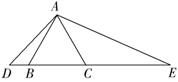试说明：
．
图1
| 得 分 | 评卷人 |
19. （本小题8分）如图，已知AB=AC,∠A=36o，AB的中垂线MN交AC于点D，交AB于点M．
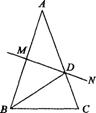有下面4个结论：
①射线BD是么ABC的平分线；②△BCD是等腰三角形；
③△ABC∽△BCD；④△AMD≌△BCD．
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明．
图2
| 得 分 | 评卷人 |
20、（本小题8分如图，在梯形ABCD中，AD∥BC，AB⊥AD，对角线BD⊥DC。
（1）求证：△ABD～△DCB；
（2）若BD=7，AD=5，求BC的长。
A D
B C
图3
| 得 分 | 评卷人 |
21． （本小题满分8分）
如图，在△ABC中，AD是BC上的高，
，
(1) 求证：AC=BD；
(2)若
，BC=12，求AD的长．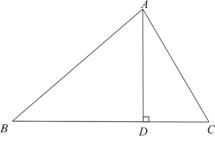
(1)证：
图4
(2)解:
| 得 分 | 评卷人 |
22．（本小题4分）如图，已知△ABC和点O.以O为位似中心，求作△ABC的位似图形，并把△ABC的边长缩小到原来的一半.
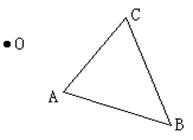
图5
| 得 分 | 评卷人 |
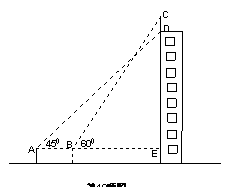23. （本小题8分）如图，某幢大楼顶部有一块广告牌CD，甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°°和60°，且A、B、E三点在一条直线上，若BE=15米，求这块广告牌的高度．(取
≈1.73，计算结果保留整数)
【解】
图6
| 得 分 | 评卷人 |
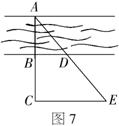24．（本小题10分）如图7，为了测量河宽，小华采用的办法是：在河的对岸选取一点
，在河的这岸选一点
，使与河的边沿垂直，然后在的延长线上取一点，并量得
米；然后又在河的这边取一点
，并量得
米；最后在射线
上取一点Ｅ，使得
，并分别量得
米．小华这种做法，她能根据已有的数据求出河宽吗？若能，请求出河宽；若不能，她还必须测量哪一条线段的长？假设这条线段的长是
米，请你用含的代数式表示河宽．
第二次月考数学参考答案及评分标准
一．选择题（本题共10小题，每小题4分，满分40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | B | B | A | D | B | C | A | C |
二．填空题（本题共6小题，每小题3分，满分18分）
11. 4cm 12.
13.
14.
;26
15.
; 
AED=B; ADE=C; 
16. △ADF～△ECF
三、解答题（共62分）
17. (本小题满分8分
(1)
(2)
－……………………4分
(3)
1∠A=30° AB=16 AC=8.
2 ∠A=∠B=45° BC= ……………………4分
18．(本小题满分8分提示：注意到
，因此
，…………………………………4分
已知式可化为
，所以．…………………………………8分
19. (本小题满分8分(1)①②③都正确…………………………………4分
（2）从①②③里面任选一个，只要合理即可（请批卷老师认真把握）…………………………………4分
20、(本小题满分8分（1）证明：因为AB⊥AD，BD⊥DC，所以∠A=∠BDC=900，因为AD∥BC，所以∠ADB=∠DBC，所以△ABD～△DCB。…………………………………4分
（2）解：△ABD～△DCB，所以AD：DB=DB：BC，因为BD=7，AD=5，所以5：7=7：BC，所以BC=
。…………………………………4分
21．(本小题满分8分）
解：(1)∵AD是BC上的高，∴AD⊥BC．
∴∠ADB=90°，∠ADC=90°． …………………………………………1分
在Rt△ABD和Rt△ADC中，
∵
=
，
=
…………………………………………3分
又已知
∴=．∴AC=BD．
………………………………4分
(2)在Rt△ADC中，
，故可设AD=12k，AC=13k．
∴CD=
=5k．
………………………………5分
∵BC=BD+CD，又AC=BD，
∴BC=13k+5k=18k ………………………………6分
由已知BC=12， ∴18k=12．∴k=．
………………………………7分
∴AD=12k=12
=8．
………8分
22．(略) (本小题满分4分)
23．(本小题满分8分解：∵AB＝8，BE＝15，∴AE＝23，在Rt△AED中，
∠DAE＝45°………………………………4分
∴DE＝AE＝23.
在Rt△BEC中，∠CBE＝60°………………………………6分
∴CE＝BE·tan60°＝
，
∴CD＝CE－DE＝－23≈2.95≈3………………………………8分
即这块广告牌的高度约为3米。
24．(本小题满分10分)根据已有的数据不能求出河宽，还需要测量
的长．………………………………5分
设
米，则由可得
，………………………………8分
设
米，则有
即
………………………………9分
．解得
．………………………………10分