函数及其图象

§1.1函数及其图象

复习目标

1.　　 各象限内点的坐标的符号特征：

点P 所在象限	一	二	三	四
横纵坐标 符　　号

2．坐标轴上点的坐标特征：

点P 所在的位置	轴	轴	原点
点P的坐标

3．对称点的坐标特征：

对称方式	关于轴 对称	关于轴 对称	关于原点 对称
点P的 对称点的坐标

4．各象限角平分线上的点的坐标特征：

⑴点P在第一、三象限角平分线上；

⑵点P在第二、四象限角平分线上。

（到两坐标轴距离相等的点都在这两条角平分线上）

5．平行于坐标轴的直线上的点的坐标特征：

⑴平行于轴的直线上的所以点的纵坐标相等；　　　　　　　　　　　　　　　 

⑵平行于轴的直线上的所以点的横坐标相等。

6．点P坐标的几何意义：

⑴点P到轴的距离为；

⑵点P到轴的距离为；

⑶点P到原点的距离为。

7．函数的有关概念：常量和变量、函数、自变量、自变量的取值范围。

8．函数的三种表示方法：解析法、列表法、图象法。

典例精析

【例1】（2005兰州）函数ｙ＝ 的自变量ｘ的取值范围是（　）
　　　Ａ．ｘ≥１且ｘ≠２ Ｂ．ｘ≠２ Ｃ．ｘ＞１且ｘ≠２ Ｄ． 全体实数

【分析】本题确定自变量ｘ的取值范围初看上去要考虑两个方面：根式与分式，但请注意根式是开三次方的，所以被开方式可取任何实数，即可取任何实数。因此只需关注分式，使其分母即可，即。

【解答】A

【例2】（2005黑龙江）在平面直角坐标系中，点P(-2，3)关于x轴的对称点在(　　)

　　A．第一象限　　B。第二象限　　C。第三象限　　D。第四象限

【分析】点P(-2，3)关于x轴的对称点的坐标为（-2，-3），而这一点在第三象限；也可以说因为点P(-2，3)在第二象限，而第二象限的点关于x轴的对称点必在第三象限。

【解答】C

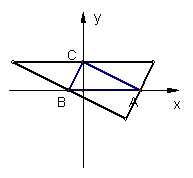【例3】（2005江苏省宿迁）已知点A（2，0）、点B（－，0）、点C（0，1），以A、B、C三点为顶点画平行四边形．则第四个顶点不可能在(　　)

C

A．第一象限　　　　　　　　　　  B．第二象限

C．第三象限　　　　 　　　　　  D．第四象限

【分析】通过画图可知，这样的点共有3个，如图。由此可知第四个顶点不可能在第三象限。

【解答】C

【例4】（2006泰州)在物理实验课上，小明用弹簧称将铁块A悬于盛有水的水槽中，然后匀速向上提起，直至铁块完全露出水面一定高度，则下图能反映弹簧称的读数y（单位N）与铁块被提起的高度x（单位cm）之间的函数关系的大致图象是(　　)

【分析】本题牵涉到自然科学的相关知识，属于学科综合题。开始时铁块A悬于水中，提起一定高度铁块A仍浸没于水中，此阶段铁块A所受的浮力不变，所以弹簧称的读数也不变；当提出水面后，铁块A所受的浮力越来越小，则弹簧称的读数越来越大；当铁块A完全被提出水面后，它所受的浮力为零，则弹簧称的读数又不变。因此选C

【解答】C

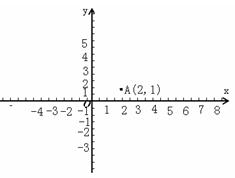
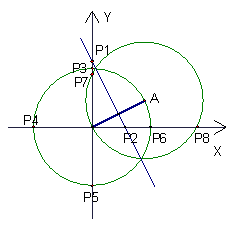
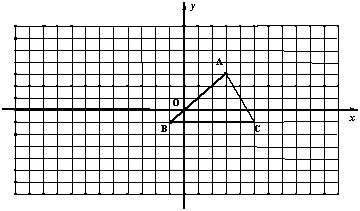
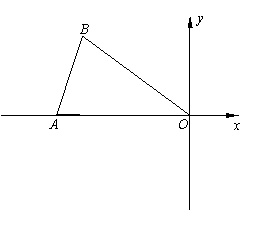
【例5】（2005年杭州）在平面直角系内，已知点A（2,1），O为坐标原点。请你在坐标轴上确定点P，使得成为等腰三角形。在给出的坐标系中把所有这样的点P都找出来，画上实心点，并在旁边标上（有个就标到为止，不必写出画法）。

【分析】本题要分情况讨论。因为不知道已有线段OA在等腰三角形AOP中是腰还是底边，所以先要分两种情况：①OA为腰②OA为底边。当OA为腰时还要注意O为顶点或A为顶点。因此本题要分三种情况讨论：①OA为底边②OA为腰且O为顶点③OA为腰且A为顶点。本题还要提醒注意的是点P是在坐标轴上，即点P可在X轴上也可以在Y轴上。

【解答】如图：这样的点共有8个。

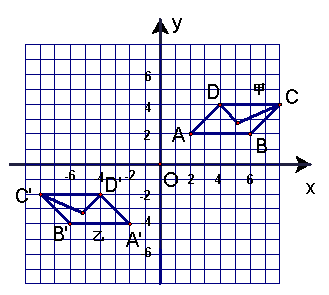
【例6】如图，（1）描述图甲变换为图乙的变换过程；

（2）设P 是图甲上的一点，求它在图乙上对应点的坐标。

【分析】A与它的对应点的坐标分别为（2，2）与（-2，-4），可见点A先作关于y轴的对称变换，再向下平移6个单位，得点。考察其他对应点可得到同样的结果。

【解答】（1）把图甲先作关于y轴的对称变换，再向下平移6个单位。

（2）当将点P作关于y轴的对称变换得：，再向下平移6个单位得：，所以图甲上的一点P在图乙上对应点的坐标。

课内巩固

1．在平面直角坐标系中，点P(3, －2)在（　　）　　　　　　　　　　　　　　　　　　　　 

A、第一象限　　B、第二象限　　　C、第三象限　　　D、第四象限

2．（2005四川泸洲）函数中，自变量的取值范围为（　　）

A．　　  　 B．　　　　 C．　　　　　 D．

3．(2005绵阳)点M(－sin60°，cos60°)关于x轴对称的点的坐标是（　　）

A．() 　　　　 　　　　　　　　　　　　　　B．(－)

C．(－,)　　　　　　　　　　　　　　　　　 D．(－,-)

4．（2005兰州）一束光线从点Ａ（３，３）出发，经过ｙ轴上点Ｃ反射后经过点Ｂ

（１，０）则光线从Ａ点到Ｂ点经过的路线长是（　　）

Ａ．４　　　 　　Ｂ．５　　　　　　  Ｃ．６ 　　　　　　Ｄ．７

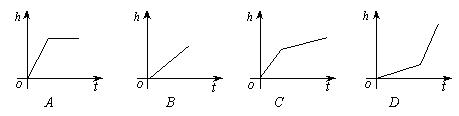
5．如图是某蓄水池的横断面示意图，分为深水池和浅水池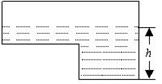，如果这个蓄水池以固定的流量注水，下面能大致表示水的最大深度h与时间t之间的关系的图像是(　　 )

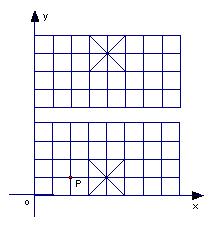
6．（2006旅顺）如图，我们给中国象棋棋盘建立一个平面直角坐标系（每个小正方形的边长均为1），根据象棋中“马”走“日”的规定，若“马”的位置在图中的点P．

⑴写出下一步“马”可能到达的点的坐标　　　　　　

　　　　　　　 　　　　　　　　　　　　　　　　 ；

⑵顺次连接⑴中的所有点，得到的图形是　　　　　　

图形（填“中心对称”、“旋转对称”、“轴对称”）；

⑶指出⑴中关于点P成中心对称的点　　　　　　　．

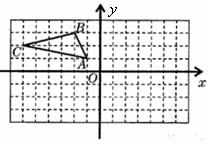7．(2006十堰)如图，在平面直角坐标系中，请按下列要求分别作出变换后的图形（图中每个小正方形的边长为个单位）：

（1）向右平移个单位；（2）关于轴对称；（3）绕点顺时针方向旋转．

8．（2006泸州）如图，在一次实践活动中，小兵从A地出发，沿北偏东45°方向行进了千米到达B地，然后再沿北偏西45°方向行进了5千米到达目的地点C。

(1)　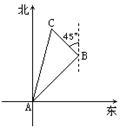求A、C两地之间的距离；

(2)　试确定目的地C在点A的什么方向？

课外拓展

A组

1. 函数y = 中自变量x的取值范围是　　　　　  。

2.（2006河北）在平面直角坐标系中，若点P（x－2，x）在第二象限，则x的取值范围为(　　 )

A．0＜x＜2　　　 B．x＜2　　C．x＞0　　　　　　 D．x＞2

3．（2004安徽）“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓缓爬行的乌龟，骄傲起来，睡了一觉。当它醒来时，发现乌龟快导终点了，于是急忙追赶，但为时已晚，乌龟还时先到达了终点……。用S₁、S₂分别表示乌龟和兔子所行的路程，t为时间，则下列图象中与故事情节相吻合的是（D　　）

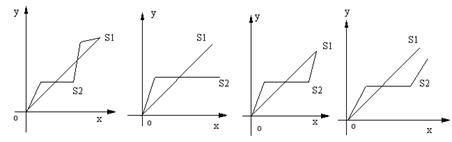A　　　　　　　　　B　　　　　　　C　　　　　　　　　D

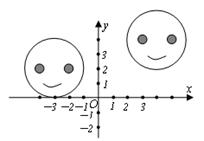
4．(2005南通)某学习小组在讨论 “变化的鱼”时，知道大鱼与小鱼是位似图形，如图。

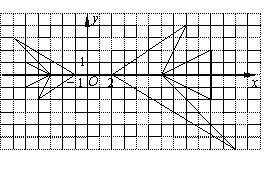则小鱼上的点（a，b）对应大鱼上的点的坐标为（　　 ）

A

A．（－2a，－2b）　　　　　B．（－a，－2b）

C．（－2b，－2a）　　　 　 D．（－2a，－b）

5．（2005南充）下列函数中，自变量x的取值范围是的是（　　）．
（A）　　　（B）
（C）　　　（D）

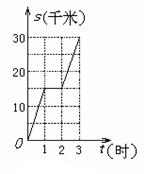6．（2005江西省）如图是某人骑自行车的行驶路程（千米）与行驶时间（时）的函数图象，下列说法不正确的是（　　 ）

A、从0时到3时，行驶了30千米　　　　B、从1时到2时匀速前进

C、从1时到2时在原地不动　　　　　  D、从0时到1时与从2时到3时的行驶速度相同

7．已知两点A。

⑴若A、B两点关于原点对称，则　　，　　；

⑵若A、B两点关于轴对称，则　　，　　；

⑶若线段AB轴,则　　，　　。

8．已知等腰三角形的周长为10厘米，将底边长表示成腰长的函数关系式是　　　　　  ，其自变量x的取值范围是　　　　　  。

9．（2006成都）如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形。在建立平面直角坐标系后，点B的坐标为。

（1）　　　 把△ABC向左平移8格后得到△，画出△的图形并写出点的坐标；

（2）　　　 把△ABC绕点C按顺时针方向旋转90°后得到△，画出△的图形并写出点的坐标；

（3）　　　 把△ABC以点A为位似中心放大，使放大前后对应边长的比为1：2，画出△

B组

10．(2005厦门)已知函数y＝－2 ，则x的取值范围是　　　　　  . 若x是整数，则此函数的最小值是　　　　　　 .

11. 如图在直角坐标系中，右边的图案是由左边的图案经过平移以后得到的。左图案中左右眼睛的坐标分别是(－4，2)、(－2，2)，右图中左眼的坐标是(3，4)，则右图案中右眼的坐标是　　　 。

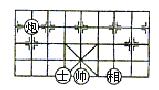12．（2005青岛） 如图，如果所在位置的坐标为（-1，-2），所在位置的坐标为（2，-2），那么，所在位置的坐标为___（-3，1）_____。

13．(2006天门)在平面直角坐标系中，设点P到原点O的距离为ρ，OP与x轴的正方向的夹角为α，则用[ρ，α]表示点P的极坐标。显然，点P的坐标和它的极坐标存在一一对应关系。如点P的坐标(1，1)的极坐标为P[，45°]，则极坐标Q[，120°]的坐标为(　　 )。

A、(－，3)　　　B、(－3， )　　　C、(，3)　　　D、(3， )

14．（2006内江）已知点P（x-1,x+3）,那么点P不可能在第　　　　象限.

15．（2005常州）某水电站的蓄水池有2个进水口，1个出水口，每个进水口进水量与时间的关系如图甲所示，出水口出水量与时间的关系如图乙所示.已知某天0点到6点,进行机组试运行,试机时至少打开一个水口,且该水池的蓄水量与时间的关系如图丙所示:

给出以下3个判断:①0点到3点只进水不出水；②3点到4点,不进水只出水；③4点到6点不进水不出水. 则上述判断中一定正确的是　　　　　　　  　　　　（　　 ）

A、①　　　　B、②　　　　C、②③　　　　D、①②③

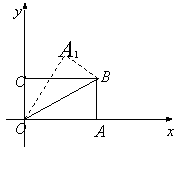
16．(2005年潍坊)如图，在直角坐标系中，将矩形沿对折，使点落在点处，已知,，则点的坐标是（ A　　　　 ）．

　　　　A．（，）　　 B．（，3）

　　　　C．（，）　　 D．（，）

17．(2005年南通)如图，在平面直角坐标系中，已知A（－10，0），B（－8，6），O为坐标原点，△OAB沿AB翻折得到△PAB．将四边形OAPB先向下平移3个单位长度，再向右平移m（m＞0）个单位长度，得到四边形O₁A₁P₁B₁．设四边形O₁A₁P₁B₁与四边形OAPB重叠部分图形的周长为l．

（1）求A₁、P₁两点的坐标（用含m的式子表示）；

（2）求周长l与m之间的函数关系式，并写出m的取值范围．

反思纠错

1．已知点P到的距离分别为2和3，则点P的坐标为　　　　　　　　　　　 .

解：点P的坐标为（2，3），（2，-3），（-2，-3）或（-2，3）。

上述答案是否正确？为什么？

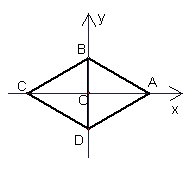2．一个菱形的较短的对角线的长为2，有一个内角是120°，取两条对角线所在的直线为坐标轴，求四个顶点的坐标。

解：如图，由已知可得都是边长为2的正三角形。而在中，，所以

。

因此菱形ABCD的四个顶点的坐标分别为：

。

上述解答是否正确？为什么？