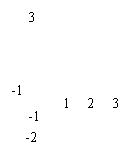初三数学第一学期期中考试（B卷）

初三数学第一学期期中考试（B卷）

数　　学

温馨提示：本次考试所有的题目都该编自作业本、教科书上例题和课后练习，希望同学们平时重视它们。

一、选择题（本题有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）

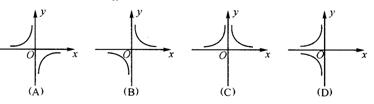
1.反比例函数的图像大致是（　 ）

2. 如果反比例函数y=的图像经过点（2，3），那么次函数的图像经过点（　 ）

  A.(-2,3)　　　  B.(3,2)　　　 C.(3,-2)　　  D.(-3,2)

3．二次函数 的图象的开口方向、对称轴、顶点坐标分别是（　　）

　A、向上；直线；（4，5）　　　B、向上；直线；（—4，5）

　C、向上；直线；（4，—5）　　D、向下；直线；（—4，5）

4．把抛物线y=3x²向右平移一个单位, 则所得抛物线的解析式为 (　 );

A. y=3(x+1)²　　 B. y=3(x-1)² 　　　C. y=3x²+1　　　　 D. y=3x²-1

5．下列说法正确的有（　　）

　（1）、相等的圆心角所对的弧相等；（2）、平分弦的直径垂直于这条弦；

（3）、长度相等的两条弧是等弧； （4）、经过圆心的每一条直线都是圆的对称轴

　 A、1个　　　 B、1个　　　C、3个　　　 D、4个

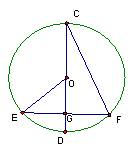
6．如图，⊙O的直径CD过弦EF的中点G，

∠EOD=40°，则∠DCF等于（ ）

A、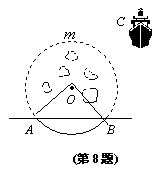80°　B、50°

  C、40°　 D、20°

7．已知扇形的弧长为2，半径为4，则此扇形的面积为（　）

A、4，　 B、5，　 C、6，　　D、8

8、如图，A、B是两座灯塔，在弓形内有暗礁，游艇C在 附　　

近海面游弋，且∠AOB=80°，要使游艇C不驶入暗礁区,则航行中

应保持∠ACB（　 ）（本题来自书上79页）

A、小于40°　　　　　 B、大于40°

C、小于80°　　　　　 D、大于80°

9．“两龙”高速公路是目前我省高速公路隧道和桥梁最多的路段．如图，是一个单心圆曲隧道的截面，若路面宽为10米，净高为7米，

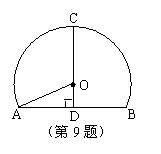则此隧道单心圆的半径是（　　　）

A.　5　　　 　　　　　　　 B. 　　　　

C. 　　　　　　　　　　 D.　7

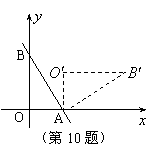10．如图，直线与轴、轴分别交于、两点，把△绕点顺时针旋转90°后得到△，则点的坐标是（　　　）

A. （3，4）　　　 　　　　 B. （4，5）　　　　　 

C. （7，4）　　　　 　　　 D. （7，3）

试卷Ⅱ

说明：本卷有二大题，14小题，共110分，请用蓝黑墨水的钢笔或圆珠笔直接在试卷上答题．

二、填空题（本题有6小题，每小题5分，共30分）

11．如果一个反比例函数的图像经过点（2，-1），那么这个反比例函数的解析式为　　　　　　　　　　　 。

12．某玩具厂计划生产一种玩具熊猫，已知每只玩具熊猫的成本为元，该厂每月生产只（取正整数），这个月的总成本为5000元，则与之间满足的关系式为▲▲▲▲。

13．二次函数的对称轴为　　　　　　　  。

14． 已知矩形的周长为10，设矩形一边长为X，它的面积为Y，则Y与X的函数关系式为　　　　　　 。

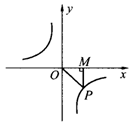
15． 如图所示，△POM的面积为2，

则该函数的解析式是_______________

 

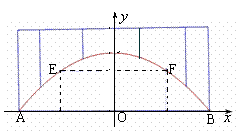16．廊桥是我国古老的文化遗产．如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为，为保护廊桥的安全，在该抛物线上距水面高为8米的点、处要安装两盏警示灯，则这两盏灯的水平距离是　　　　　　 米（精确到1米）．

三、解答题（本题有8小题，共80分）

17、（本题9分）请用三种不同的方法找出下图中各圆的圆心（每画出一种给3分画图工具不限，但要保留画图痕迹

18．（本题7分）你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y (m)是面条的粗细(橫截面积)s(㎜²)的反比例函数，其图象如图所示。

(1)写出y与s的函数关系式；

(2)求当面条粗1.6㎜²时，面条的总长度是多少？

19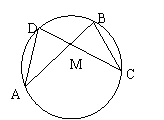．（本题8分）如图，AB=CD，AB与CD相交于点M。

求证：

（1）　　　 AD=CB；

（2）　　　 （2）AM=CM。（本题该编自作业本（1）20面）

21．（本题8分）一个球从地面上竖直向上弹起时的速度为，经过 时球的高度为。已知物体竖直上抛运动中，（表示物体运动上弹开始时的速度，表示重力系数，取）。问

（1）、球从弹起至回到地面需多少时间？

（2）、经过多少时间球的高度达到？（本题来自书上49页）

20、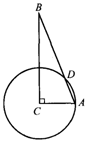（本题8分）如图，在△ABC中，∠ACB=90⁰，∠B=15⁰, 以点C为圆心， CA长为半径的圆C交AB于点D, 且AC=6 .

(1）求的度数；

(2)求的长度．

22．（本题12分）

　　已知抛物线 经过点A（1，0），B（0，-4）。

（1）、求此抛物线的解析式；

（2）、当x 取何值时，y随x的增大而增大？

（3）、若抛物线与x轴的另一个交点为C，求△ABC的面积。

23．（本题12分）

某商场以每件30元购进一种商品，试销中发现每天的销售量（件）与每件的销售价（元）满足一次函数。

　　（1）写出商场每天的销售利润（元）与每件的销售价（元）之间的函数关系式；

　　（2）如果商场要想获得最大利润，每件商品的销售价定为多少元为最合适？最大销售利润为多少元？

24．（本题14分）

小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：

复习日记卡片

内容：一元二次方程解法归纳　　　　　　　　　　　　　　　  时间：2007年6月×日

举例：求一元二次方程的两个解

方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解 　　解方程：． 　　解：

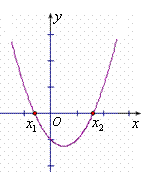
方法二：利用二次函数图象与坐标轴的交点求解 如图所示，把方程的解看成是二次 函数　　　　　　　  的图象与轴交点的 横坐标，即就是方程的解.

方法三：利用两个函数图象的交点求解 　　　　（1）把方程的解看成是一个二次函数　　　　　　　　  的图象与一个一次函数　　　　　　　　　  图象交点的横坐标；  （2）画出这两个函数的图象，用在轴上标出方程的解.