初三数学调研摸拟测试卷
本卷共8大题28小题，满分120分，考试时量120分钟
1—12题答案均写在答题卡上，写在试卷上无效。
| 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 合计 |
一、选择题(每小题2分，共24分)
1．已知等腰三角形的一个底角等于30°，则这个等腰三角形的顶角等于（ ）
A．150° B．120° C．75° D．30°
2．方程
的解是（ ）．
A．
B．
C．
D．
3．关于x的方程x2－2x＋k＝0有解，则k的值可以是( ).
A．
B．
C．2
D．
4．用配方法将方程
=0变形，结果正确的是 （ ）．
A．
=0 B．
=0
C．
=0 D．）
=0
5．已知菱形的两条对角线长分别为4cm和10cm，则菱形的边长为（ ）
A．116cm B．29cm C．
cm D．
cm
6．在一个四边形ABCD中，依次连结各边中点的四边形是菱形，则对角线AC与BD需要满足条件（ ）
A．垂直 B．相等 C．相交 D．不再需要条件
7．两直角边分别为3，4的直角三角形斜边上的高为（ ）．
A．3 B．4 C．5 D．
8．已知∠AOB＝90°，点P在∠AOB的平分线上， OP＝6，则点P到OA、OB的距离为( )
A．6、6 B．3、3 C．3、
3
D． 3、3
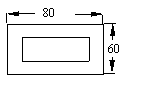9．如图，从一块长方形铁片中间截去一个小长方形，使剩下部分四周的宽度都等于x，且小长方形的面积是原来长方形面积的一半，则x的值为（
）
A．10 B．60 C．10或60 D．20或30
10．平行四边形、矩形、菱形、正方形都具有的性质（ ）
A．对角线相等 B．对角线互相平分
C．对角线平分一组对角 D．对角线互相垂直
11．如图，在长为5cm，宽为3cm的长方形内部有一平行四边形，它的面积等于（ ）
A．5 cm2 B．6 cm2 C．7 cm2 D．6.5 cm2
12．商场服装柜在销售中发现：某童装平均每天可售出20件，每件盈利40元.为了迎接“六一”国际儿童节，商场决定采取适当的降价措施，调查发现：如果每件童装降价4元，那么平均每天就可多售出8件.要想平均每天销售这种童装共盈利1200元，设每件童装降价x元，那么应满足的方程是（ ）．
A．(40+x) (20-2x) =1200 B．(40-2x) (20+x) =1200
C．(40-x) (20+2x) =1200 D． (40+2x) (20-x) =1200
二、填空题(每小题3分,共12分)
13．等腰三角形的周长为7，一边长为1，则它另两边长分别为 ．
14．是关于x的方程
的解，则a=
．
15．等腰三角形一腰上的高与另一腰的夹角为30°，若腰长为2，则腰上的高为 ．
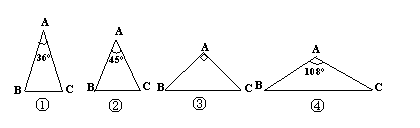
16．如图所示，在下列三角形中，若AB=AC，则能被一条直线分成两个小等腰三角形的
是 （填序号）．
三、(每题6分，共24分)
17．解方程
（1）
（2）
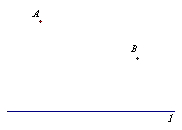18．己知A、B两个电话分机离电话线l的距离如图所示，试用尺规在直线l确定一点P，使得点P到A、B两个电话分机的距离相等．
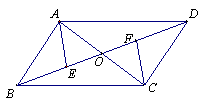19．在平行四边形ABCD中，对角线AC、BD相交于点O，点E、F在BD上，且BE＝DF，连结AE、FC，那么AE与FC有何关系？为什么？
20．某农户种植花生，原来种植的花生亩产量为
千克，出油率为
（即每
千克花生可加工成花生油
千克）.现在种植新品种花生后，每亩收获的花生可加工成花生油
千克，其中花生出油率的增长率是亩产量增长率的
，求新品种花生亩产量的增长率.
四、(每小题6分，共12分)
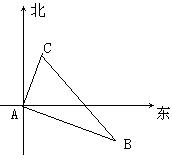
21．甲、乙两船同时从港口A出发，甲船以12海里/时的速度向北偏东35°航行，乙船向南偏东55°航行。2小时后，甲船到达C岛，乙船到达B岛，若C、B两船相距40海里，问乙船的速度是每小时多少海里？
22． 如图，有一地面为长方形的仓库，一边长为5m，现在将它改建为简易住房，改建后分为客厅、卧室和卫生间三部分，其中客厅和卧室都为正方形，若已知卫生间的面积为6平方米，试求长方形仓库的另一边的长．
五、(第23题7分，第24题8分，共15分)
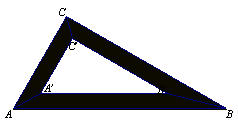
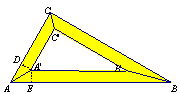
23．如图，一块含有30º角（∠ABC=30º，∠ACB=90º）的木制三角板是由三块宽度相等的木条拼合而成，若木条的宽度为5cm，求制作时拼合缝AA’的长．
 |
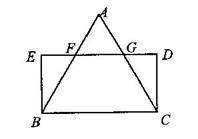24．已知：如图，△ABC中，AB=AC，矩形BCDE的边DE分别与AB、AC交于点F，G。求证：EF=DG.
六、(每小题8分，共16分)
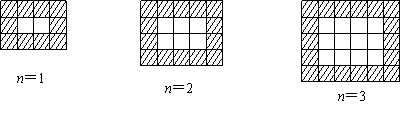
25．如图，用同样规格黑白两色的正方形瓷砖铺设矩形地面，观察下列图形并解答有关问题：
（1）在第n个图中，共有 块白色瓷砖，共有 块黑色瓷砖（均用含n的代数式表示）；
（2）若铺设这样的矩形地面共用了506块瓷砖，通过计算求此时n的值；
（3）是否存在n，使得黑瓷砖与白瓷砖块数相等的情形？说明理由。
 |
26． 在劳技课上，老师请同学们在一张长为17cm，宽为16 cm的长方形纸板上剪下一个腰长为10cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合，其余两个顶点在长方形的边上)。请你帮助同学们设计出不同类型的，你认为符合条件的等腰三角形，(分别在下列矩形中画出示意图)并分别计算剪下的等腰三角形的面积。(位置不同，形状全等的将视为一种结果)
 |  | ||
七、(本题8分)
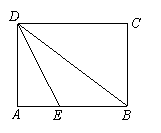27．如图，折叠矩形纸面ABCD，先折出折痕（对角线）BD，再折叠，使AD落在对角线BD上，得折痕DE，若3AB＝4BC，AE＝1，求AB的长．
八、(本题9分)
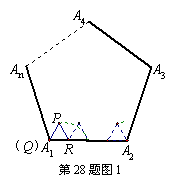28．阅读：我们把边长为1的等边三角形PQR沿着边长为整数的正n（n＞3）边形的边按照如图1的方式连续转动，当顶点P回到正n边形的内部时，我们把这种状态称为它的“点回归”；当△PQR回到原来的位置时，我们把这种状态称为它的“三角形回归”．
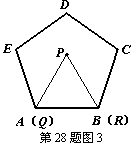
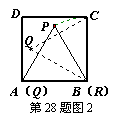例如：如图2，边长为1的等边三角形PQR的顶点P在边长为1的正方形ABCD内，顶点Q与点A重合，顶点R与点B重合，△PQR沿着正方形ABCD的边BC、CD、DA、AB……连续转动，当△PQR连续转动3次时，顶点P回到正方形ABCD内部，第一次出现P的“点回归”；当△PQR连续转动4次时△PQR回到原来的位置，出现第一次△PQR 的“三角形回归”．
操作：如图3，如果我们把边长为1的等边三角形PQR沿着边长为1的正五边形ABCDE的边连续转动，则连续转动的次数
k= 时，第一次出现P的“点回归”；连续转动的次数k= 时，第一次出现△PQR 的“三角形回归”．
猜想：
我们把边长为1的等边三角形PQR沿着边长为1的正n（n＞3）边形的边连续转动，
（1）连续转动的次数k= 时，第一次出现P的“点回归”；
（2）连续转动的次数k= 时，第一次出现△PQR 的“三角形回归”；
（3）第一次同时出现P的“点回归”与△PQR 的“三角形回归”时，写出连续转动的次数k与正多边形的边数n之间的关系．
[参考答案]
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | C | A | B | D | B | D | D | A | B | C | C |
二、13．3、3； 14．±1； 15．
； 16．①③④
三、17．（1）
，
（2）
18．作线段AB的垂直平分线与l的交点为点P。
19．AE=FC，AE∥FC
在□ABCD中，AO=OC，BO=DO。…………（2分）
∵BE＝DF， ∴EO＝FO。∵∠AOE=∠COF， ∴△AOE≌△COF。……（4分）
∴AE=FC，…………（5分）
∠AEO=∠CFO。
∴AE∥FC。…………（6分）
（其它解法参照给分）
20．解：设新品种花生亩产量的增长率为x，………………………（1分）
根据题意得：
………………………（4分）
解得
，………………………（5分）
（不合，舍去）
答：新品种花生亩产量的增长率为20%………………………（6分）
四、(每小题6分，共12分)
21．乙船的速度是16海里/时。…………………（6分）
22．设长方形的另一边的长为x米 …………………………（1分）
由题意得：（x -5）[5 -(x -5)]=6， …………………………（3分）
整理得：x2 -15x+56=0，解之得：x1=7，x2=8 ， ………………（5分）
x1，x2都符合题意．
答：长方形的另一边的长为7米或8米．…………………（6分）
五、(第23题7分，第24题8分，共15分)
23．过点A’作A’D⊥AC于点D，过点A’作A’E⊥AB于点E．…………1分
∵木制三角板是由三块宽度相等的木条拼合而成，∴A’D＝A’E．
∴AA’平分∠CAB．…………3分
∵∠ABC=30º，∠ACB=90º，∴∠CAB=60º．∴∠DAA’=30º
∵∠ADA’=90º，∴DA’=
AA’． …………6分
∵木条的宽度为5cm，∴DA’=5cm，∴AA’ =10cm．…………7分
24．证明：∵AB=AC，∴∠ABC=∠ACB………… (2分)
又∵四边形BCDE是矩形，∴BE=DC，∠E=∠D=∠EBC=∠BCD=90°……(4分)
∴∠EBF=∠DCG 。
∴△BEF≌△CDG …………(6分)
∴EF=DG ………… (8分)
（其它解法参照给分）
六、(每小题8分，共16分)
25．（1）n（n+1），4n +6；………… (2分)
（2）n（n+1）+4n +6=506………… (3分)
解得n1=20，n2=-25（不合题意，舍去），
所以n的值为20。………… (5分)
（3）由题意得n（n+1）=4n +6，………… (6分)
………… (7分)
因为不是正整数，所以不存在黑瓷砖与白瓷砖块数相等的情形。………… (8分)
26． 解：
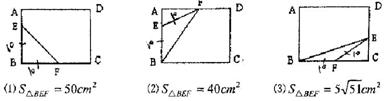
画出一个且面积计算正确得3分，两个得6分，三个得8分。
七、(本题8分)
27．解：设AB=4x，∵3AB＝4BC，∴BC=3x。………… (1分)
过点E作EF⊥BD，垂足为F。………… (2分)
在矩形ABCD，由折叠得BD=AD=BC= 3x，∴BD=5x。∴BF=2x。………… (4分)
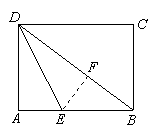∵AE＝1，∴BE=4x-1。
在R△BEF中，EF2+BF2=BE2。12+(2x)2=(4x-1)2………… (7分)
解得x1=
，x2=0（不合题意，舍去），
所以AB=
。………… (8分)
八、(本题9分)
28．操作：3，5………………………………………4分
猜想：（1）3 …………………………………6分
（2）n……………………………………………8分
（3）当n不是3的倍数时，k=3n
当n是3的倍数时，k=n………………………………………9分