初三数学上学期测试卷
一、精心选一选（每题3分，共30分）
1、若反比例函数
的图象经过点（2，－3），则图象必经过另一点（ ）
A、（２，３） B、（－２，３） C、（３，２） D、（－２，－３）
2、抛物线
向右平移1个单位，再向上平移2个单位，得到新的图象的二次函数表达式是( )
A.
B.
C.
| |
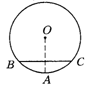
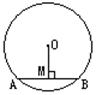
3、如图，⊙O的直径为10，圆心O到弦AB的距离OM的长为4，则弦AB的长是（ ）
A．3 B．6 C．4 D．8
4、等边三角形的外心在它的…………………………………………………（ ）
|
|
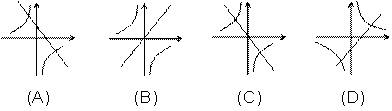
5、在同一坐标系中函数
和
的大致图象是（ ）
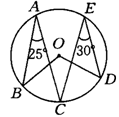
6．图中∠BOD的度数是（ ）
A．55° B．110° C．125° D．150°
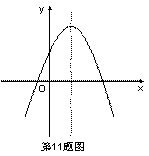
7、已知二次函数
的图象如图所示，则一次函数
的图象不经过（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
8、一条弦分圆周为5：7，这条弦所对的圆周角的度数是…………………（ ）
A．
B．
C．
D．
9、根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| y=ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
判断方程ax2+bx+c=0（a≠0,a、b、c为常数）一个解的范围是 （ ）
Ａ、3＜x＜3.23 Ｂ、3.23＜x＜3.24 Ｃ、3.24＜x＜3.25 Ｄ、3.25＜x＜3.26
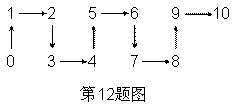
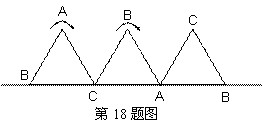
10、探索规律：根据下图中箭头指向的规律，从2004到2005再到2006，箭头的方向是（ ）
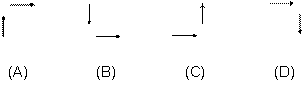
二、专心填一填（每题3分，共24分）
11、一条弧的度数是
，所对的圆周角是 。
12、在函数
中，自变量x的取值范围是___________________。
13、某三角形三边长分别为
，则此三角形外接圆的面积为 。
14、
请写出一个开口向上，且对称轴为直线
的二次函数解析式 。
15、如图所示
，则反比例函数的解析式是
。
16、已知抛物线
的顶点在
轴上，则
的值是
。
17、经市场调查，某种商品的进价为每件6元，专卖商店的每日固定成本为150元。当销售 价为每件10元时，日均销售量为100件，单价每降低1元，日均销售量增加40个。设单价为x元时的日均毛利润为y元，则y关于x的函数解析式为_____________________。（只需列式）
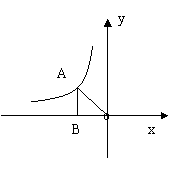18、如图所示，一块等边三角形的木板，边长为1，现将木板沿水平线翻转，那么B点从开始到结束所走过的路径长度为 。
 | |||
| |||
三、耐心做一做（共66分）
| |
19、（6分）求二次函数y=x2+2x-4图象的开口方向、对称轴、顶点坐标。分别求当x满足什么条件时y>0,y<0，y=0。
|
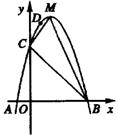21、(8分)如图，二次函数y=ax2+bx+c(a≠0)的图像与x轴交于A、B两点，其中A点坐标为(―l，0)，点C(0，5)，D(1，8)在抛物线上，M为抛物线的顶点。
(1)求抛物线的解析式；
(2)求△ACB的面积。
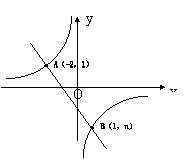22、(本题8分) 如图，一次函数
的图象与反比例函数
的图象相交于A、B两点，（1）利用图中条件，求反比例函数和一次函数的解析式（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
23.（本题8分）下图是一个残破的圆片示意图.
（1）请找出该残片所在圆的圆心O的位置（保留画图痕迹，不必写画法）；
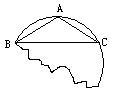（2）若此圆上的三点A、B、C满足AB=AC，BC=2，且∠ABC=30°，求弧BAC的长.
24、（本题9分）如图，△ABC内接于⊙O，CM⊥AB于M，CN是直径，F为
的中点，
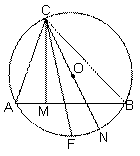求证：CF平分∠MCN。
25、（9分）在直角坐标平面中，O为坐标原点，二次 函数
的图象与x轴的负半轴相交于点C（如图5），点C的坐标为（0，－3），且BO＝CO
（1）求出B点坐标和这个二次函数的解析式；
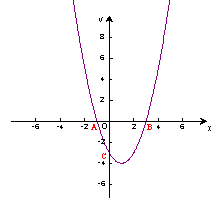（2）求△ABC的面积。
（3）设这个二次函数的图象的顶点为M，求AM的长.
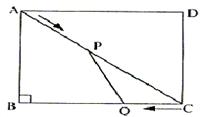
26、(本题12分) 如图，在矩形ABCD中，AB＝6米，BC＝8米，动点P以2米/秒的速度从点A出发，沿AC向点C移动，同时动点Q以1米/秒的速度从点C出发，沿CB向点B移动，设P、Q两点移动t秒（0＜t＜5）后，四边形ABQP的面积为S米2。
（1）求面积S与时间t的关系式；
（2）在P、Q两点移动的过程中，四边形ABQP与△CPQ的面积能否相等？
|
