相似三角形的应用
(检测时间50分钟 满分100分)
班级______ 姓名______ 得分____
一、基础训练:(每小题12分,共48分)
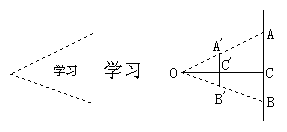
1.如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字感觉相同(即视角相同)?毛
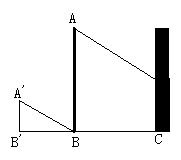
2.如图所示,在离某建筑物4m处有一棵树,在某时刻,1.2m长的竹竿垂直地面, 影长为2m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上,墙上的影高为2m,那么这棵树高约有多少米?
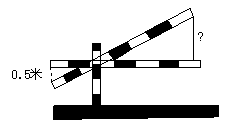
3.如图所示,铁道口的栏杆短臂长1米,长臂长16米,当短臂端点下降0.5米时, 长臂端点升高了几米?
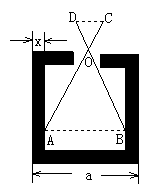
4.如图所示,零件的外径为a,要求它的厚度x,需要求出内孔的直径AB, 但不能直接量出AB,现用一个交叉钳(两臂长AC和BD相等)去量,如果OA:OC=OB:OD=n,且量得CD=b,求厚度x.
二、提高训练:(每小题16分,共32分)
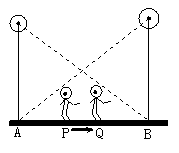
1.如图所示,小华在晚上由路灯A走向路灯B,当他走到点P时, 发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时, 发现他身前影子的顶部刚好接触到路灯B的底部,已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离;
(2)当小华走到路灯B时,他在路灯A下的影长是多少?
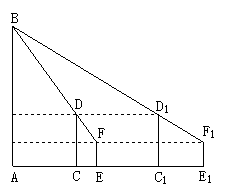
2.如图所示,学校的围墙外有一旗杆AB,甲在操场上C处直立3m高的竹竿CD, 乙从C处退到E处恰好看到竹竿顶端D与旗杆顶端B重合,量得CE=3m, 乙的眼睛到地面的距离FE=1.5m,丙在C1处也直立3m高的竹竿C1D1,乙从E处退后6m到E1处, 恰好看到两根竹竿和旗杆重合,且竹竿顶端D1与旗杆顶端B也重合,量得C1E1=4m,求旗杆AB的高.
三、中考题与竞赛题:(共20分)
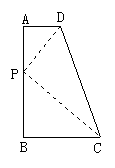
如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.
答案:
一、
1.解:如图所示,有△OAB∽△OA′B ′,
量得课本正文中的字的大小为0.4cm×0.35cm,
∴字高A′B′=0.4cm,因此![]() ,
,
又∵OC=500cm,OC′=30cm,
∴AB=![]() (cm),
(cm),
同理字的宽度为![]() ≈6(cm),
≈6(cm),
∴老师黑板上的字的大小应为7cm×6cm(高×宽).
2.4.4m. 3.8米. 4.![]() .
.
二、1.(1)18m. (2)3.6m. 2.10.5m.
三、解:(1)若点A,P,D分别与点B,C,P对应,即△APD∽△BCP,
∴![]() ,
,
∴![]() ,
,
∴AP2-7AP+6=0,
∴AP=1或AP=6,
检测:当AP=1时,由BC=3,AD=2,BP=6,
∴![]() ,
,
又∵∠A=∠B= 90°,∴△APD∽△BCP.
当AP=6时,由BC=3,AD=2,BP=1,
又∵∠A=∠B=90°,
∴△APD∽△BCP.
(2)若点A,P,D分别与点B,P,C对应,即△APD∽△BPC.
∴![]() ,∴
,∴![]() , ∴AP=
, ∴AP=![]() .
.
检验:当AP=![]() 时,由BP=
时,由BP=![]() ,AD=2,BC=3,
,AD=2,BC=3,
∴![]() ,
,
又∵∠A=∠B=90°,∴△APD∽△BPC.
因此,点P的位置有三处,即在线段AB距离点A1、![]() 、6 处.毛
、6 处.毛