一.解答题
1.如图5，△ABC内接于⊙O，AB=AC，直线XY切⊙O于点C，弦BD∥XY，AC、BD相交于
点E。 ⑴求证：△ABE≌△ACD；⑵若AB=6cm，BC=4cm，ED=2cm, 求AE的长。
 |
2、如图，AB是⊙O的直径，弦CD⊥AB于P。
⑴已知：CD=8cm，∠B=30°，求⊙O的半径；
⑵如果弦AE交CD于F，求证：AC2=AF·AE.
3、如图，AB切⊙O于B，OA交⊙O于C，若AO=
，AB=2，
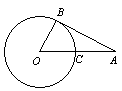求⊙O半径，并求tanA的值。
4、如图，AB切⊙O于B，OA交⊙O于C，∠A=300，若⊙O半径为3cm，求AO的长。
5、已知四边形ABCD外切于⊙O，四边形ABCD的面积为24，周长24，求⊙O的半径。
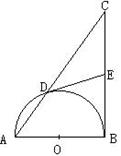
6、如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE.
(1) DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；
(2) 若AD、AB的长是方程x2－10x+24=0的两个根，求直角边BC的长。
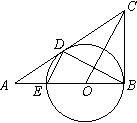
7、已知：如图，在△ABC中，∠ABC＝90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，连结DB、DE、OC。
⑴从图中找出一对相似三角形（不添加任何字母和辅助线），并证明你的结论；
⑵若AD＝2，AE＝1，求CD的长。
8、已知：如图，⊙O1、⊙O2相交于A、B、PE切⊙O1于P，PA、PB交⊙O2于C、D.求证:CD∥PE.
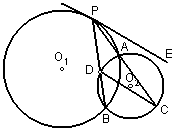
9、已知：如图47-3，⊙O1与⊙O2相交于A、B，若两圆半径分别为12和5， O1O2=13，求AB的长.
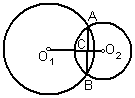
10、已知：⊙O1与⊙O2外切于P，AC是过P点的割线交⊙O1于A，交⊙O2于C，BC切⊙O2于C，过点O1作直线AB交BC于B.求证：AB⊥BC.
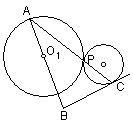
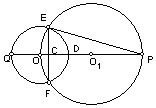11、如图，⊙O1经过⊙O的圆心，E、F是两圆的交点，直线OO1交⊙O于点Q、D，交⊙O1于点P，交EF于点C，且EF=
，sin∠P=
（1）求证：PE是⊙O的切线；（2）求⊙O和⊙O1的半径的长；
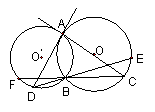
12、已知：如图，⊙O和⊙O’相交于A、B两点，AC是⊙O’的切线，交⊙O于C点，连结CB并延长交⊙O’于点F，D为⊙O’上一点，且∠DAB＝∠C，连结DB交延长交⊙O于点E。①求证： FD∥CA；②若BF＝4，CA＝
，求CB的长。
 |
13、已知：矩形ABCD中，CD=2，AD=3，P是AD上的一个动点，且和A、D不重合，过P作PE⊥CP
交直线AB于E，设PD=x， AE=y。写出y关于x的函数解析式，并写出x的取值范围。
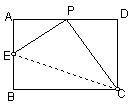
14. 
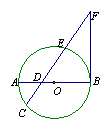如图，AB为⊙O直径，BF⊥AB于B点，割线FEC交AB于D点，AD=2，CD=3，ED=4．求EF的长．
15、如图，A为⊙O外一点，过A作两条直线分别与⊙O交于B、C和D、E点．若BE为⊙O直径，AB=12，DE=30，AD=BC．求∠A的度数和BE的长．
16、如图，在△ABC中，以BC为直径的⊙O交AB于D点，交AC于E点，AD=3，
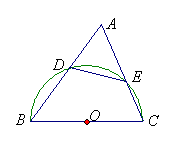S△ADE=S四边形BCED，CE＝
。求：(1)∠A；(2)∠B的正弦值．
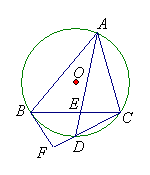17、如图，已知⊙O内接△ABC，D为
中点，AD交BC于E点，过B作⊙O的切线交CD延长线于F点，AE=3，DE=1，BF=
。求CF的长．
二.证明题：
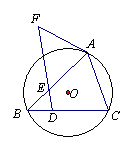1．如图，已知⊙O的内接ΔABC，D在BC上，过D点作AC的平行线交AB于E点，交过A的直线于F点，且BE·AE=DE·EF。求证：AF是⊙O的切线。
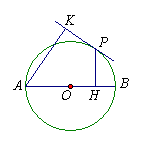2．如图，AB为⊙O直径，自圆上一点P作AB的垂线PH，垂足为H，自点A向过P点的切线作垂线，垂足K。求证：AH＝AK。
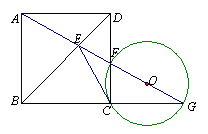
3、如图，由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G，
求证：CE是△CGF的外接圆⊙O的切线。
 |
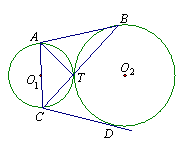
4、如图，⊙O1与⊙O2外切于T，AB为公切线，BT的延长线交⊙O1于点C，CD切⊙O2于点D。
求证：① AC为⊙O1的直径；② AC＝CD。
 |