圆的有关性质
知识要点
1、 圆是平面上到 的距离等于 的点的集合。
2、 的三点确定一个圆；任何一个三角形都有一个外接圆，外接圆的圆心叫做三角形的 心，它是三角形的 的交点。
3、 圆是以为 轴的轴对称图形，又是以 为中心的中心对称图形。
4、 垂径定理的条件是 ，结论是 。
5、 在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦心距中，有一组量相等，那么它们所对应的其余各组量都 。
典型考题
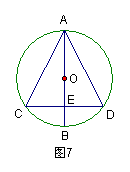
例1、如图1，在⊙O中，圆心角∠AOB＝120°，弦AB＝
，则⊙O的半径是 。
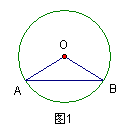
例2、如图2，已知AB为⊙O的直径，且AB⊥CD，垂足为M，CD＝8，AM＝2，则OM＝ 。
例3、⊙O的半径是5，P是圆内一点，且OP＝3，则过点P的最长弦是 ，最短弦是 。
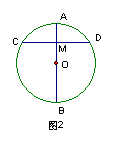
例4、如图3，AB是⊙O的直径，CD是弦，若AB＝10㎝，CD＝8㎝，那么A、B两点到直线CD的距离之和为（ ）㎝。
A、12 B、10 C、8 D、6
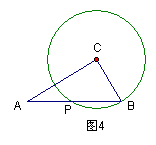
例5、如图4，在Rt△ABC中，∠C＝90°，AC＝
，BC＝1，若以C为圆心、CB的长为半径的圆交AB于P，则AP＝ 。
同步训练
1、在直径为20㎝的圆中，弦心距是6㎝的弦长是 ㎝。
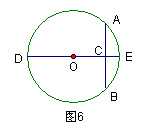
2、如图6，DE是⊙O的直径，弦AB⊥DE，垂足为C，若AB＝6，CE＝1，则CD＝ ，OC＝ 。
3、圆的弦与直径相交成30°角，并且分直径为8㎝和2㎝两部分，则弦心距等于 ㎝。
4、AB是⊙O的直径，弦CD⊥AB于P（P在OB上），CD＝
，OP＝2，则AC的长是（ ）
A、 B、
C、
D、
5、若⊙O中，弦AB与直径CD垂直，垂足为E，且AE＝4，CE＝2，那么⊙O的半径等于（ ）
A、5 B、
C、 D、
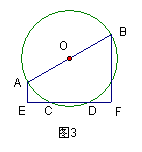
6、如图7，如果AB是⊙O直径，弦CD⊥AB，垂足为E，那么下列结论中，错误的是（ ）
A、CE＝DE B、
C、∠BAC＝∠BAD D、AC＞AD
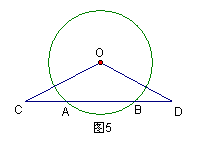
7、如图5，在⊙O中，AB为⊙O的弦，C、D是AB上的两点，且AC＝BD，
求证：△OCD是等腰三角形。
