圆中考题选
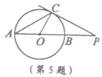
1．(2006年浙江省绍兴市) 已知00的直径AB与弦AC的夹角为35。，过C点的切线 PC与AB的延长线交于点P，则么P等于
A．150 B．200 C．250 D．300
2．(2006年重庆市)⊙O的半径为4，圆心O到直线
的距离为3，则直线与⊙O的位置关系是（ ）
A.相交 B.相切 C.相离 D. 无法确定
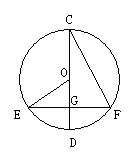
3．(2006年重庆市)如图，⊙O的直径CD过弦EF的中点G，∠EOD=40°,则∠DCF等于（ ）
A.80° B. 50° C. 40° D. 20°
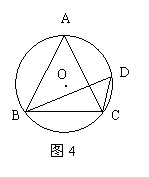
4．（2006年大连市）如图4，在⊙O中，∠ACB＝∠D＝60°，AC＝3，则△ABC的周长为_________。
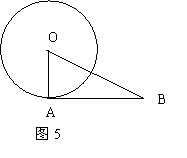
5．（2006年大连市）如图5，AB是⊙O的切线，OB＝2OA，则∠B的度数是__________。
 | |||
 | |||
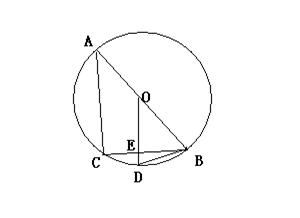
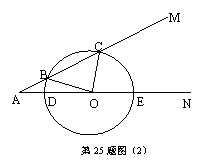
6．（江西省）如图，AB是⊙0的直径，BC是弦，OD⊥BC于E，交
于D。
（1）请写出四个不同类型的正确结论；
（2）连结CD，设∠CDB＝α，∠ABC＝β，试找出α与β之间的一种关系式，并予以证明。
7．
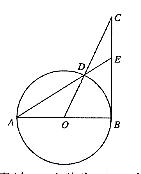（2006年长春市）如图，AB为⊙O直径，BC切⊙O于B，CO交⊙O交于D，AD的延长线交BC于E，若∠C
= 25°，求∠A的度数。
解：∵AB为⊙O的直径，BC切⊙O于B，∴∠ABC = 90°，
∵∠C = 25°，∴∠BOC = 65°
∵∠A = 
∠BOD，∴∠A = 32.5°
8．（2006年海淀区）如图，已知A、B、C在⊙O上，∠COA＝100°，则∠CBA＝（ ）B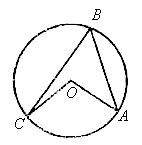 
A. 40° B. 50° C. 80° D. 200°
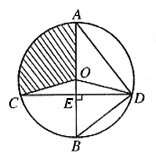
9．（2006年海淀区）如图，已知⊙O的直径AB垂直于弦CD于E，连结AD、BD、OC、OD，且OD＝5。
（1）若
，求CD的长；
（2）若 ∠ADO：∠EDO＝4：1，求扇形OAC（阴影部分）的面积（结果保留
）。
解：
解：（1）因为AB是⊙O的直径，OD＝5， 所以∠ADB＝90°，AB＝10，在Rt△ABD中，
， 又，所以
，所以
，
，因为∠ADB＝90°，AB⊥CD，所以
，所以，
，所以
， 所以
。
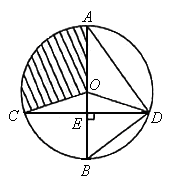（2）因为AB是⊙O的直径，AB⊥CD，所以
， 所以∠BAD＝∠CDB，∠AOC＝∠AOD，因为AO＝DO，所以∠BAD＝∠ADO，所以∠CDB＝∠ADO，设∠ADO＝4x，则∠CDB＝4x，由∠ADO：∠EDO＝4：1，则∠EDO＝x，因为∠ADO＋∠EDO＋∠EDB＝90°，所以
，所以x＝10°，所以∠AOD＝180°－（∠OAD＋∠ADO）＝100°， 所以∠AOC＝∠AOD＝100°，
。
10．（2006年海淀区）如图，在⊙O中，弦AC与BD交于E，
，求CD的长。
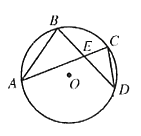解：
解：因为弦AC与BD交于E，所以A、B、C、D是⊙O上的点
所以∠B＝∠C，∠A＝∠D， 所以△ABE∽△DCE， 所以
，
所以
，所以
。
11．（2006年旅顺口区）若圆锥的底面周长为20π，侧面展开后所得扇形的圆心角为120°，则圆锥的侧面积为 ．300π；
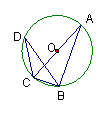12．（2006年旅顺口区）如图，点D在以AC为直径的⊙O上，如果∠BDC＝20°，那么∠ACB＝ ． 70°；
13．（2006年旅顺口区）如图，AB与⊙O切于点B，AO＝6㎝，AB＝4㎝，则⊙O的半径为 （ ） B
A、4
㎝ B、2㎝ C、2
㎝ D、㎝
14．（2006年贵阳市）如图3，⊙O是等边三角形ABC的外接圆，点D是⊙O上一点，则∠BDC = ；60
15．（2006年贵阳市）如她4，B是线段AC上的一点，且
，分别以AB、AC为直径画圆，则小圆的面积与大圆的面积之比为
；4：25
16．（2006年江西省南昌市）如图AB是⊙O的直径，BC是⊙O弦OD⊥CB于点E，交
于点D
（1）请写出三个不同类型的正确结论：
(2)连结CD，设∠CDB=
，∠ABC=
，试找出与之间的一种关系式并给予证明.
(1)不同类型的正确结论不惟一．以下答案供参考：
①BE=CE 
②，③∠BED=90°④∠BOD=∠A，
⑤AC∥OD
⑥AC⊥BC ⑦
⑧
⑨ΔBOD是等腰三角形⑩ΔBOE∽ΔBAC等，
（2) 与的关系式主要有如下两种形式，请参照评分：
①答；与之间的关系式为-=90°
证明：∵AB为⊙O的直径，∴∠A+∠ABC=90°，又∵四边形ACDB为圆的内接四边形，∴∠A+∠CDB=180°∴∠CDB-∠ABC=90°，即- = 90°。 说明：关系式写成 = 90°+或=-90°均参照给分
②答与之间的关系式为；>2
证明 ∵ OD=OB ， ∴∠ODB=∠ OBD，又∵∠ OBD=∠ABC+∠CBD ∴∠ODB>∠ABC
∵OD⊥BC
∴
∴CD=BD，∴∠CDO=∠ODB=
∠CDB，∴∠CDB>∠ABC，>2。说明：若得 出与与的关系式为>，且证明正确的也给满分
17．（06年江西省南昌市）两圆半径分别为5和3，圆心距为8，则两圆的位置关系是【 】C
A内切 B相交 C外切 D外离
18．
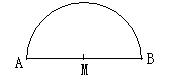（2006年南安市）如图，半圆M的直径AB为20cm，现将半圆M绕着点A顺时针旋转180°．（1）请你画出旋转后半圆M的图形；（2）求出在整个旋转过程中，半圆M所扫过区域的面积（结果精确到1cm
）．
⑴画图略 ；⑵ 半圆M所扫过的面积＝×∏×20+×∏×10 ＝250∏≈758（cm）。
19．(2006年泰州市)半径分别为6
和4的两圆内切，则它们的圆心距为 
.
20．(2006年泰州市)已知：∠MAN=30°，O为边AN上一点，以O为圆心、2为半径作⊙O，交AN于D、E两点，设AD=
，
⑴如图⑴当取何值时，⊙O与AM相切；
⑵如图⑵当为何值时，⊙O与AM相交于B、C两点，且∠BOC=90°．
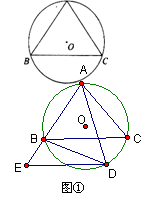
(2006年苏州市) 如图①，△ABC内接于⊙0，且∠ABC＝∠C，点D在弧BC上运动．过点D作DE∥BC．DE交直线AB于点E，连结BD． (1)求证：∠ADB=∠E； (2)求证：AD2=AC·AE； (3)当点D运动到什么位置时，△DBE∽△ADE请你利用图②进行探索和证明
A
A
 |
证：∵DE∥BC，∴∠ABC=∠E，∵∠ADB, ∠C都是AB所对的圆周角,
∴∠ADB=∠C， 又∠ABC=∠C， ∴∠ADB=∠E
(2) ∵∠ADB=∠E，∠BAD=∠DAE． ∴△ADB∽△AED ∴
,即AD2=AB·AE
∵∠ABC=∠C，∴AB=AC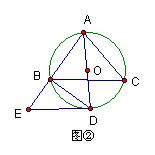
∴AD2=AC·AE
(3)点D运动到弧BC中点时．△DBE∽△ADE， ∵DE∥BC．∴∠EDB=∠DBC．
∵∠DBC所对的是弧DC, ∠EAD所对的是弧DB， ∴∠DBC=∠EAD, ∴∠EDB=∠EAD
又∠DEB=∠AED， ∴△DBE∽△ADE
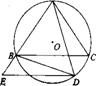
（06年连云港市）（本小题满分10分）如图，⊙O是等腰三角形ABC的外接圆，AB=AC，延长BC至点D，使CD＝AC，连接AD交⊙O与点E，连接BE、CE与AC交于点F。
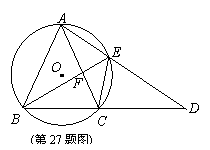（1）求证：△ABE≌△CDE；
（2）若AE=6，DE=9，求EF的长。