九年级数学第一学期期中试题卷4
一、 选择题:(本题共10小题,每小题4分,满分40分)
1、一元二次方程![]() 的一般形式是( )。
的一般形式是( )。
 (A)
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
|
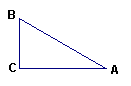
则BC的长为( )。
(A)4cm
(B)2cm
(C) ![]() cm
(D)
cm
(D)![]() cm
cm
3、质量为50千克的物体,它的密度ρ关于体积V的函数关系式为( )
(A) ρ=![]() (B) ρ= 50V (C) ρ=
(B) ρ= 50V (C) ρ=![]() (D) ρ=50+V
(D) ρ=50+V
4、已知四边形的两条对角线相等,那么,顺次连接四边形各边中点得到的四边形是( )
(A) 菱形 (B) 矩形 (C) 梯形 (D) 正方形
5、反比例函数![]() 的图像大致是( )
的图像大致是( )
(A)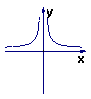 (B)
(B) 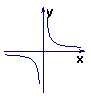 (C)
(C) 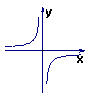 (D)
(D)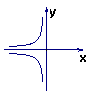
6、“圆柱与球的组合体”如右图所示,则它的三视图是( )
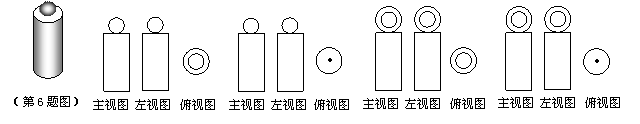
A. B. C. D.
7、下列命题中,真命题有( )个。
(1)斜边对应相等的两个直角三角形全等。(2)顶角对应相等的两个等腰三角形全等。
(3)两腰对应相等的两个等腰三角形全等。(4)两条直角边对应相等的两个直角三角形全等。
 A. 1 B. 2 C. 3 D. 4
A. 1 B. 2 C. 3 D. 4
8、如图,□ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A、4 cm B、6cm C、8cm D、10cm
9、若一元二次方程(m-1)x2+3m2x+(m2+3m-4)=0有一根为零,则m=( )
 A. 1
B. -4 C. 1或-4 D. -1或4
A. 1
B. -4 C. 1或-4 D. -1或4
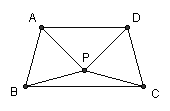
10、如图,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD.有下列四个结论:①∠PBC=15°;②AD∥BC;③直线PC与AB垂直;④四边形ABCD是轴对称图形.其中正确的结论的个数为( )
A.1 B.2 C.3 D.4
二、填空题:(请将正确答案写在对应横线上,本题有6小题,每空5分,满分30分)
11、在△ABC中,若AB=AC,∠B=50°,D是BC的中点,则∠CAD=_________度.
12、方程x(2x+3)=0的根是_________________.
13、菱形的两条对角线长分别是8和6,则这个菱形的边长为________.
14、在阳光明媚的星期天上午,小明和他父亲到沙滩上散步。小明发现他自己身高1.50m,在阳光下影长1.20m。其父亲身高1.70m,则此时其父亲的影长为___________m。
15、已知关于x的方程![]() 的一个根为
的一个根为![]() ,则a的值是____________.
,则a的值是____________.
16、两个反比例函数![]() 在第一象限内的图像如图,点
在第一象限内的图像如图,点![]()
在反比例函数![]() 图像上,它们的横坐标分别是
图像上,它们的横坐标分别是![]() ,
,
纵坐标分别是1,3,5,![]() 共2005个连续奇数,过点
共2005个连续奇数,过点![]()
分别作![]() 轴的平行线,与
轴的平行线,与![]() 的图像交点依次是
的图像交点依次是
![]() ,则
,则![]()
三、解答题: (满分80分)
17、用合适的方法解下列方程(每小题5分,共15分)
(1) ![]() (2)
(2)![]() (3)
(3)
![]()
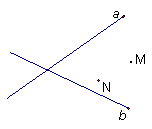
18(7)a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场。现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等。请用尺规画出O点位置,不写作法,保留痕迹。
19、(7分)已知关于x的一元二次方程![]()
请选取一个你喜爱的m的值,使方程有两个不相等的实数根,并验证它的正确性.
(即求出方程的根,方法不限)
20、(7)如图,点O是矩形ABCD的两对角线的交点,已知∠COD=120°,AC=10cm。
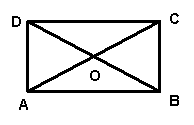 求矩形ABCD的面
求矩形ABCD的面
21、(8)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。若商场平均每天要盈利1200元,每件衬衫应降价多少元?
22、(8分)已知:反比例函数y =![]() (k≠0)图象上的某一点坐标满足方程
(k≠0)图象上的某一点坐标满足方程![]() ,(1)求k的值;
,(1)求k的值;
(2)这个反比例函数的图像与一次函数y=-3x的图像相交吗?若相交,求出所有交点坐标;若不相交,请说明理由.
23(12分) 已知:△ABC中AB=AC,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.(1)写出图中与△ABC相似的三角形;(2分)
(2)求证:MP+MQ=AB;(5分)
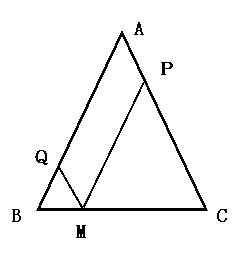 (3)当M位于BC的什么位置时, 四边形AQMP是菱形?在图2中画出图形并予以证明。(5分)
(3)当M位于BC的什么位置时, 四边形AQMP是菱形?在图2中画出图形并予以证明。(5分)
(图1) (图2)
24、(14分)已知:如图所示,在直角坐标系内有一条直线和一条曲线,这条直线和x轴y轴分别相交于点A和点B,且OA=OB=1,这条曲线是函数![]() 的图象在第一象限内的一个分支,点P是这条曲线上任意一点,它的坐标是(a,b),由点P向x轴、y轴所作的垂线PM、PN(点M、N为垂足)分别与直线AB相交于点E和点F。
的图象在第一象限内的一个分支,点P是这条曲线上任意一点,它的坐标是(a,b),由点P向x轴、y轴所作的垂线PM、PN(点M、N为垂足)分别与直线AB相交于点E和点F。
(1)设 交点E、F都在线段AB上,分别求点E、F 的坐标。
(2)求⊿EOF的面积。(用a、b的代数式表示)
(3)⊿AOF与⊿BOE一定相似吗?如果一定相似,请予以证明;如果不一定相似或者一定不相似,请简要说明理由。
(4)点P在曲线上移动时,⊿OEF随之变动,指出在⊿OEF的三个内角中,大小始终保持不变的那个角的大小,并证明你的结论。
九年级数学第一学期期中试题卷4
一、 单项选择题:(每小题4分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(本题有6小题,每小题5分,共30分)
11._______ __ 12.______ ____ 13.________ ___
14.______ __ 15.______ ____ 16._______ ____
三、解答题(共80)
17、解方程(每题5分,共15分)
(1)
![]() (2)
(2)![]() (3)
(3) ![]()
18(7)a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场。现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等。请用尺规画出O点位置,不写作法,保留痕迹。

19、(7分)已知关于x的一元二次方程![]()
请选取一个你喜爱的m的值,使方程有两个不相等的实数根,并验证它的正确性.
(即求出方程的根,方法不限)
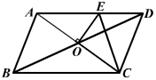
 20、(7)已知:在梯形ABCD中,AD∥BC,CA平分∠DCE,AB⊥AC,E为BC的中点。求证:DE、AC互相垂直平分。
20、(7)已知:在梯形ABCD中,AD∥BC,CA平分∠DCE,AB⊥AC,E为BC的中点。求证:DE、AC互相垂直平分。
21、(8)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。若商场平均每天要盈利1200元,每件衬衫应降价多少元?
22、(8分)已知:反比例函数y =![]() (k≠0)图象上的某一点坐标满足方程
(k≠0)图象上的某一点坐标满足方程![]() ,(1)求k的值;
,(1)求k的值;
(2)这个反比例函数的图像与一次函数y=-3x的图像相交吗?若相交,求出所有交点坐标;若不相交,请说明理由.
23(12分) 已知:△ABC中AB=AC,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.(1)写出图中与△ABC相似的三角形;(2分)
(2)求证:MP+MQ=AB;(5分)
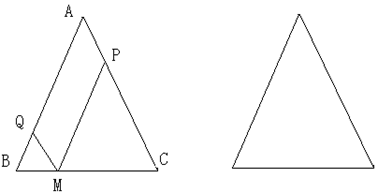 (3)当M位于BC的什么位置时, 四边形AQMP是菱形?在另一图中画出图形并予以证明。(5分)
(3)当M位于BC的什么位置时, 四边形AQMP是菱形?在另一图中画出图形并予以证明。(5分)
24、(14分)已知:如图所示,在直角坐标系内有一条直线和一条曲线,这条直线和x轴y轴分别相交于点A和点B,且OA=OB=1,这条曲线是函数![]() 的图象在第一象限内的一个分支,点P是这条曲线上任意一点,它的坐标是(a,b),由点P向x轴、y轴所作的垂线PM、PN(点M、N为垂足)分别与直线AB相交于点E和点F。
的图象在第一象限内的一个分支,点P是这条曲线上任意一点,它的坐标是(a,b),由点P向x轴、y轴所作的垂线PM、PN(点M、N为垂足)分别与直线AB相交于点E和点F。
(1)设 交点E、F都在线段AB上,分别求点E、F 的坐标。
(2)求⊿EOF的面积。(用a、b的代数式表示)
(3)⊿AOF与⊿BOE一定相似吗?如果一定相似,请予以证明;如果不一定相似或者一定不相似,请简要说明理由。
(4)点P在曲线上移动时,⊿OEF随之变动,指出在⊿OEF的三个内角中,大小始终保持不变的那个角的大小,并证明你的结论。