九年级数学 第一学期期中质量检测试卷4
第一学期期中质量检测试卷4
(考试时间:100分钟 分值:150分)
| 题号 | 一(1-10) | 二(11-16) | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 总分 |
| 分值 | |||||||||||
| 得分 | |||||||||||
| 阅卷人 |
一、选择题(本大题有10小题.每小题4分.共40分.请选出每小题中一个符合题意的正确选项,不选、多选、错选.均不给分):
1、下列运算正确的是 ( )
A、x10÷x5=x2; B、x-4·x=x-3;
C、x3·x2=x6; D、(2x-2)-3=-8x6
2、若分式![]() 的值为零,则x的值是
( )
的值为零,则x的值是
( )
A、2或-2 B、2 C、-2 D、4
3、不改变分式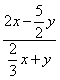 的值,把分子、分母中各项系数化为整数,结果是
( )
的值,把分子、分母中各项系数化为整数,结果是
( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
4、一元二次方程x2-4=0的解是 ( )
A、x=2 B、x=2,x=-2
C、x=-2
D、x1= ![]() , x2=-
, x2=-![]()
5、若关于y的一元二次方程ky2-4y-3=3y+4有实根,则k的取值范围是 ( )
A、k>-![]() B、k≥-
B、k≥-![]() 且k≠0
且k≠0
C、k≥-![]() D、k>
D、k>![]() 且k≠0
且k≠0
6、若两圆半径分别为R和r(R>r),圆心距为d,且R2+d2=r2+2Rd, 则两圆的位置关系为 ( )
A、内切 B、内切或外切
C、外切 D、相交
7、一圆锥的侧面展开后是扇形,该扇形的圆心角为120°,半径为6cm,则此圆锥的表面积为 ( )
A、4πcm2 B、12πcm2 C、16πcm2 D、28πcm2
8、关于x的一元二次方程x2+kx-1=0的根的情况是 ( )
A、有两个不相等的同号实数根 B、有两个不相等的异号实数根
C、有两个相等的实数根 D、没有实数根
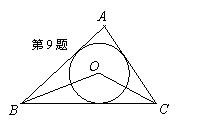
9、如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC= ( )
A、130° B、100° C、50° D、65°
|
10、钟老师出示了小黑板上的题目,如图,小敏回答:“方程有一根为1”,小聪回答:“方程有一根为2”。则你认为 ( )
A、只有小敏回答正确 B、只有小聪回答正确
C、小敏、小聪回答都正确 D、小敏、小聪回答都不正确
二、填空题(本大题有6小题.每小题5分.共30分):
11、生物学家发现一种病毒的长度约为0.mm,则它的长度用科学记数法表示为 (结果保留两个有效数字)。
12、当m=______时,方程![]() 会产生增根。
会产生增根。
 13、某农场原计划用m天完成A公顷的播种任务,如果要提前a天结束,那么平均每天比原计划要多播种_________公顷.
13、某农场原计划用m天完成A公顷的播种任务,如果要提前a天结束,那么平均每天比原计划要多播种_________公顷.
14、钟表的轴心到分针针端的长为5cm,那么经过40
分钟,分针针端转过的弧长是 。
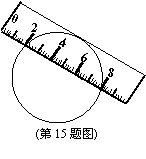
15、如图,一宽为2cm的刻度尺在圆上移动,当刻
度尺的一边与圆相切时,另一边与圆两个交点处的
读数恰好为“2”和“8”(单位:cm),则该圆的半径
为 cm。
16、在⊙O中,圆心角∠AOC=1000,则圆周角∠ABC的度数为 。
三、解答题:(本大题有8小题,第17~20小题每小题8分.第2l小题10分,第22、23小题每小题12分.第24小题14分,共80分.解答需写出必要的文字说明、演算步骤或证明过程)
17、计算或化简:
①(![]() )-2-(2-π)0+|-3| ②
)-2-(2-π)0+|-3| ② ![]()
 18、解方程:①x2-2x-3=0
②
18、解方程:①x2-2x-3=0
② ![]()
19、已知关于x的方程x2-(2k+1)x+k2-1=0
(1)若方程有实数根,求k的取值范围;
(2)若x1,x2是方程的两根,且x12+x22=9,求k的值。
20、如图,AB为半圆O的直径,C、D是半圆上的三等分点,若⊙O的半径为1,E为线段AB上任意一点,计算图中阴影部分的面积。
 |
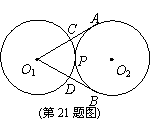
21、如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长之和为
 |
22、截至目前,我国退耕还林工程试点扩到20多个省、区、市,具体情况见下表(单位:万公顷)
| 基本情况 | 造林绿化面积 | 退耕还林面积 | 宜林荒山荒坡造林面积 |
| 2003年完成 | 88.50 | 39.89 | 48.61 |
| 2004年新增 | 227 | 266 |
① 将上表补充完整; ②若2006年新增绿化面积是2004年的两倍,求2005年、2006年的平均增长率(精确到0.1%)。
 23、阅读材料:如图(一),ΔABC的周长为
23、阅读材料:如图(一),ΔABC的周长为![]() ,内切圆O的半径为r,连结OA、OB、OC,ΔABC被划分为三个小三角形,用S△ABC表示ΔABC的面积
,内切圆O的半径为r,连结OA、OB、OC,ΔABC被划分为三个小三角形,用S△ABC表示ΔABC的面积
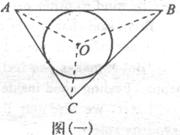 ∵ S△ABC=SΔOAB+SΔOBC+SΔOCA
∵ S△ABC=SΔOAB+SΔOBC+SΔOCA
又∵S△OAB=![]() ,S△OBC=
,S△OBC=![]() ,
,
S△OCA =![]()
∴S△ABC=![]() +
+![]() +
+![]() =
=![]() (可作为求三角形内切圆半径公式)
(可作为求三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
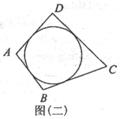
(2)类比与推理:若四边形ABCD存在内切圆,如图(二)且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
 |
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
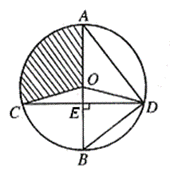
24、如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
(1)若![]() ,求CD的长;
,求CD的长;
(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留![]() )。
)。
 |
参考答案:
一、选择题:
BCDBB BCBAC
二、填空题
11、4.5×10-5mm
12、-3
13、![]()
14、![]() 15、13/4
16、500
或1300
15、13/4
16、500
或1300
三、解答题:
17、(1)11 (2)1
18、(1)x1=3 x2=-1 (2)x=2
19、(1)K≥-5/4 (2)K=1
20、π/6
21、2π
22、(1)493 (2)41.4%
23、(1)![]() (2)
(2)![]() (3)
(3)![]()
24、(1)48/5
(2) ![]()