九年级数学第一学期质量检测试卷

题号	一	二	21	22	23	24	25	26	27	28	总分
得分
阅卷人

九年级数学第一学期质量检测试卷

同学们：要认真审题、仔细答题、不要漏题，祝你考试成功！

一、选择题（每题3分，共30分）

1、如图，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是（　　 ）

A、同位角　　B、内错角　 C、对顶角　 D、同旁内角

2、等边三角形的对称轴有　　　　　　　　　　　　　　　　　　  （　 　　　）

A、1条　 B、2条　　C、3条　　　D、4条

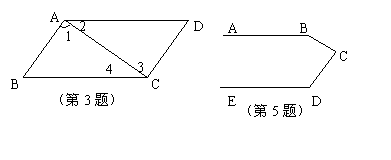
3、如图，若AB∥DC，那么　　　　　　　　　　　　　　　　  （　　　　）

A、∠1=∠3　　　　B、∠2=∠4　　C、∠B=∠D　 　　 D、∠B=∠3

4、等腰三角形的顶角的外角为70°，那么一个底角的度数为　　（　　　  ）

A、35°　　　B、55°　　　 C、65°　　　　D、110°

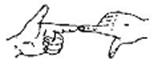
5、如图，已知AB∥ED，则∠B+∠C+∠D的度数是　　　　　  （　　　　  ）

A、180°　 B、270°　C、360°  D、450°

6、边长分别是下列各组数的三角形中，能组成直角三角形的是　（　　　　 ）

A、5，10，13．　 B、5，7，8。　 C、7，24，25。　　D、8，25，27。

7、一天，小明的爸爸送给小明一个礼物，小明打开包装后，画出它的主视图与

俯视图如图所示，根据小明画的视图，请你猜礼物是　　　　 （　　　　）

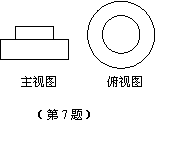A．钢笔　　B．生日蛋糕　　

C．光盘　　D．一套衣服

8．下列各图中，不是直四棱柱的表面展开图的是（　　）

　　　

 

9、八年级（1）班50名学生的年龄统计结果如表所示，则此班学生年龄的众数、中位数分别为　　（　　 ）

年龄	13	14	15	16
人数	4	22	23	1

　(A)14，14　　 (B)15，16　　　

(C)14，15　　 (D)15，14

10、如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若AB=10，AC=6，则△ACD的周长为（　　 ）

A、16　　B、14　　C、20　　D、18

二、填空题：（每空格3分，共30分）

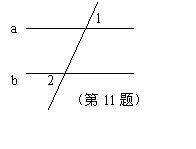
11、如图，若a∥b，∠1=40°，则∠2=　　　　度；

12、样本-2，-1，0，3，5的平均数是　　　　　　　　  。

13、已知一个等腰三角形的两边长分别是2和5，那么这个等腰三角形的周长为　　　　　　　  ；

14、已知一个直三角形的两直角边分别是3，4，则此直角三角形的斜边上的中线长是　　　　　 。

15、已知一个等腰三角形腰上的高与底边的夹角为37°，则这个等腰三角形的顶角等于　　　　　度.

16、已知a,b,c的方差是4，则数据3a+2,3b+2,3c+2的标准差是　　　　  。

17、如图∠A=90°，∠B=15°，BD=DC=4，则AC=　　　　　　 。

18、如图，要为一段高为5米，长为13米的楼梯铺上红地毯，则红地毯至少

要　　　　　　 米长。

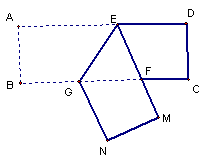
19、如图，把一长方形纸片ABCD沿EG折叠后，点A、B分别落在M、N的位置上，EM与BC相交与点F，已知∠BGE=110º，则∠EFG=　　　　  度

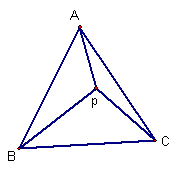
20、如图P为等边△ABC内一点，且PA=3，PC=4，PB=5，则∠APC=　　　　度。

三、解答题：（40分）

21、如图，∠1=100°，∠2=100°，∠3=120°，求∠4的度数。（7分）

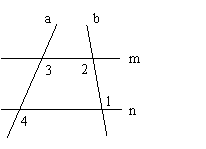解：∵∠1=∠2=100°（已知）

∴　　　　∥　　　 （　　　　　　　　　　　　  ）

∴∠　　　=∠　　　（　　　　　　　　　　　　  ）

又∵∠3=120°（已知）

∴∠4=　　　　 度

22、如图，一根竹竿在离地面某处断裂，竹竿顶部落在离竹竿底部12米处，已知竹竿原长18米，试求出竹竿在离底部什么位置断裂的。（6分）

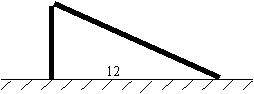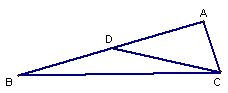
23、如图，AD是等腰△ABC的底边BC上的中线，过点D作DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由。（6分）

24.老师计算学生的学期总评成绩时按照如下的标准：平时作业占10%，单元测验占30%，期中考试占25%，期末考试占35%。小丽和小明的成绩如下表所示：

学生	平时作业	单元测验	期中考试	期末考试
小丽	80	75	71	88
小明	76	80	70	90

请你通过计算，比较谁的学期总评成绩高？（6分）

25、已知等边△ABC和点P，设点P到△ABC3边的AB、AC、BC的距离分别是h₁，h₂，h₃，△ABC的高为h，若点P在一边BC上（图1），此时h=0，可得结论h₁+h₂+h₃=h，请你探索以下问题：

　　当点P在△ABC内（图2）和点P在△ABC外（图3）这两种情况时，h₁、h₂、h₃与h之间有怎样的关系，请写出你的猜想，并在（2）或（3）中选择一个简要说明理由．

　　 　　　 

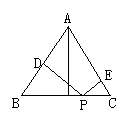
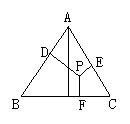
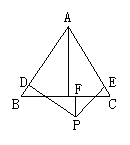
　　　　　　　 (1)　　　　　　　　　  (2)　　　　　　　　　　  (3)

26、如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，

（1）求证：△BCE≌△DCF;　　（4分）

（2）若AB=21，AD=9，BC=CD=10，求AC的长。　　（4分）

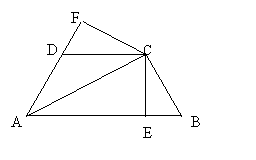四、提高题（第27题4分，第28题6分，共10分）

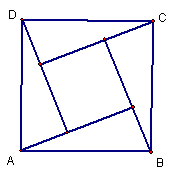
27、2002年8月，在北京召开的国际数学家大会会标取材于我国数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图），如果大正方形的面积是13，小正方形的面积是5，直角三角形的较短直角边为a，较长直角边为b，则=　　　　　　　 .

28、已知：如图，△ABC中，AB=AC=3，（i=1,2,3,…,2006）是底边BC上2006个不同的点，若(i=1,2,3,…,2006)，

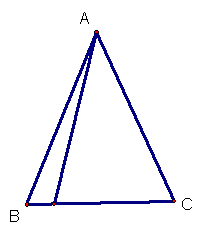
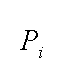求：　的值。